高三模拟练考题（二）
一、选择题（每小题5分，共60分，且每小题只有一个正确答案，请把正确答案写在题的括号内）.
1、设
则
（ ）
A．Q=P B.
Q
P
C. P
Q = {2,4}
D .PQ = {(2,4)}
2、若f(x)=
与f
(x)都经过(1,2)点, ,则f(x)与f(x)图象的交点个数 ( )
A. 1 B. 2 C. 3 D. 不确定
3、圆台母线长为5，两底面半径之比为
侧面展开图扇环圆心角为216
，则此圆台体积是
（ ）
A. 
B.
C.
D. 
4、
是锐角三角形的两个内角，M= 
,N=
+
,R=Sin
+Sin，则M、N、R的大小关系是
（ ）
A. MNR B.
RNM C.MRN D.RMN
5、已知
+
+(1+
)
=
+ 
x+…+
x,
若+
+
=29-n,那么自然数N的值是
（ ）
A. 4 B.3 C.6 D.5
6、已知X，Y为正实数，且X，a
，a
，Y成等差数列，X，b，b，Y成等比数列，则
的取值范围
（ ）
A. [4,+
） B.
(0 ,4) C.
R D.
(-,0]
[4,+ )
7、设复数Z=
，则Z的模与辐角主值分别是 （ ）
A. 2 ，
B.
32 ， 
C.
32 , 
D.32，
8.在
ABC中，SinA：SinB：SinC=3：2：4，则
的值为 （ ）
A. 
B.
C.-
D.
9、
（ ）
A．—1 B.0 C.1 D.2002
10.已知
范围
是 （ ）
A．
B.
C.
D.
11、（理）已知极坐标方程
所表示的曲线是
（ ）
A．圆 B.椭圆 C.双曲线的一支 D.抛物线
（文）双曲线
的一个焦点到一条渐近线的距离等于
（ ）
Ａ.
B.3
C.4
D.2
12、旅客列车每天18：07由上海站出发，驶往乌鲁木齐，50小时可以到达，每天10：09从乌鲁木齐返回上海。为保证在上海与乌鲁木齐乘车区间内每天各有一列火车发往对方站，至少需要准备这种列车的列数为 （ ）
A 4 B 5 C 6 D 7
二、填空题（每小题4分，共16分，请把正确答案填写在空格处.）.
13、不等式
的解集为
.
14、空间内五个点中的任意三个都不共线，用这五个点为顶点只构造出了四个三棱锥，则这五个点最多可以确定 个平面.
15、已知平行直线
与同心圆系
的交点为
当
取最小值时，
的取值为
.
16、给出函数：①
；
②
；
③
.
则不同时满足性质：（a）对于任意
；
（b）图像关于点（1，0）对称的函数序号为 .
三、解答题：
17、(12分)（理）若不等式
对满足
的所有ｍ都成立，试求ｘ的取值范围．
(12分)（文）已知
，解不等式
.
18、（12分）已知函数
.
(1)化简
的解析式；
（2）若
，求
使为偶函数；
（3）在（2）成立的条件下，求满足=1 且 
的ｘ集合．
19、（12分）四棱锥
底面是边长为4的正方形，高PA=3.E、F分别为
、
中点.(1) 求证：AF
;(2)求平面PAD和平面PCE所成的角.
20.某公司取消福利分房和公费医疗,[实际年薪制工资结构改革,该公司从而2000年起,每人的工资由三个项目组成并按下表规定实施:
| 项目 | 金额(元/人年) | 性质与计算方法 |
| 基础工资 | 10000 | 从2000年起每年递增10%,与工龄无关 |
| 房屋补贴 | 400 | 按职工到公司的年限计算,每年递增400元 |
| 医疗费 | 1600 | 固定不变 |
如果该公司今年有5位职工,计划从明年起每年新招5名职工.
(1)若2000年算第一年,试把第n年该公司付给职工工资总额y(万元)表示成年人限n的函数.
(2)试判断公司每年发给职工工资总额中,房屋补贴与医疗费总和能否超过基础工资总额的20%.
21、（12分）（理）已知平行四边形ABCD，A
.
(1) 求平行四边形对角线交点E的轨迹；
(2)
过A作直线交以AB为焦点的椭圆于M、N两点且
的中点到
轴距离为
，求椭圆方程.
（12分）（文）已知双曲线方程为
，一个椭圆以坐标轴为对称轴，离心率是双曲线离心率的倒数，焦距是双曲线的焦点到渐近线的距离，求椭圆方程.
22、（14分）已知点的序列
中点，
是线段
中点
是线段
中点.
（1）、写出
之间关系式.
(2)、设
，由此猜出数列
通项公式，并证明.
(3)、求当
时的值.
参考答案：
一、1 B； 2 C； 3 A； 4 A； 5 A； 6 A； 7D； 8A； 9B； 10B； 11(理)D，
（文）C； 12B.
二、13 ，
； 14， 7； 15，
； 16， ②，③ .
三、17.（理）解：变形原不等式得：
由已知有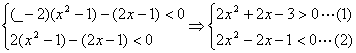
解（1）与（2）得：
（文）解：由已知得
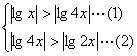
，由
并解之得：
18.解：（1）由题得
（2）当
时，
为偶函数.
（3）由
得
所求的集合为
19.（1）证明：设PC的中点为G，连结EG、FG，
四边形AEGF为平行四边形，
.
不含于平面PCE，而EG含于平面PCE，
（2）解：延长DA、CE交于点M，则PM是所求二面角的棱，过点A作
连结ET.
根据三垂线定理有
，
是所求二面角的平面角.
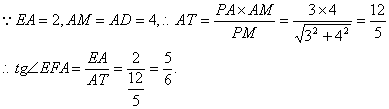
20.解: (1)房屋补贴
（万元）,
基础工资5n
(万元).
依题意有
(万元)
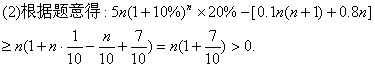
故职工房屋补贴与医疗费的总和不超过基础工资总额的20%.
21.(理科)
解:设E(x,y),连结OE,则
,即E的轨迹是半径为1、以原点为圆心、除去点
的圆.
(2)由圆锥曲线统一定义可知,
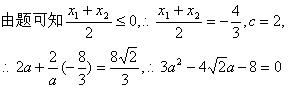
解之得
椭圆的方程为
（文科）解：双曲线
，
焦点到渐近线的距离为3.
所以，椭圆的离心率
焦距
故所求椭圆方程为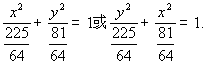
22.解
根据题意,当
时,
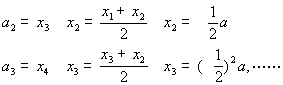
由此猜想:
下边予以证明:
且
所以数列
是公比为
的等比数列.
当时,
由
知数列是公比为的等比数列,
