高三年级第一次月考答案数学试卷
一、选择题(每小题4分,共48分)
1、若![]() ,则
,则![]() ( D )
( D )
A.0 B。4 C.。6 D。8
2、等比数列![]() 中,Tn表示前n项的积,若T5=l,则 ( B )
中,Tn表示前n项的积,若T5=l,则 ( B )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3、等差数列![]() 中,
中,![]() ,
,![]() ,则其公差d的值为
( B )
,则其公差d的值为
( B )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4、若四个正数a,b,c,d成等差数列,x是a和d的等差中项,y是b和c的等比中项,则x和y的大小关系是 ( D )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5、已知等比数列![]() 的各项均为正数,公比
的各项均为正数,公比![]() Q=
Q=![]() ,则P与Q的大小关系是
( A )
,则P与Q的大小关系是
( A )
A.P>Q B.P<Q C.P=Q D.无法确定
6、一张报纸,其厚度为a,面积为b,现将此报纸对折(既沿对边中点的连线折叠)7次,
这时报纸的厚度和面积分别是 ( C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7、等差数列![]() 的前n项和分别为
的前n项和分别为![]() 与
与![]() ,若
,若![]() ,则
,则![]() 的值是( D )
的值是( D )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8、某赛季足球比赛的计分规则为:胜一场,得3分;平一场,得1分;负一场,得0分.一球队打完15场比赛,积33分.若不考虑顺序,该队胜、平、负的情况共有( A )
A 3种 B 4种 C 5种 D 6种
9、有6个座位连成一排,现安排3个人就座,则恰好有两个空位相连的不同座法有( C )
A 36种 B 48种 C 72种 D 96种
10、下面四个判断中,正确的是 ( C )
A. 式子![]() (n∈
(n∈![]() ),当n=1时,恒为1;
),当n=1时,恒为1;
B. 式子![]() (n∈
(n∈![]() ),当n=1时,恒为
),当n=1时,恒为![]() ;
;
C. 式子![]() …+
…+![]() (n∈
(n∈![]() ),当n=1时恒为
),当n=1时恒为![]() ;
;
D.设f(![]() )=
)=![]() (n∈
(n∈![]() ),f(k+1)=f(k)+
),f(k+1)=f(k)+![]() .
.
11、数列1、3、6、10、…的一个通项公式是 ( C )
A.an=![]() B.an=n2-1 C.an=
B.an=n2-1 C.an=![]() D.an=
D.an=![]()
12、如果函数![]() 对任意的实数
对任意的实数![]() ,都有
,都有![]() ,那么
,那么![]() 、
、![]() 、
、![]() 的大小关系是
( D )
的大小关系是
( D )
A.![]() >
>![]() >
>![]() B.
B. ![]() <
<![]() <
<![]()
C. ![]() <
<![]() <
<![]() D.
D. ![]() <
<![]() <
<![]()
二、填空题(每小题4分,共16分)
13、当![]() 时,
时,![]() 的最 大 值为
的最 大 值为 ![]() 。
。
14、如不等式![]() 和
和![]() 同时成立,则
同时成立,则![]() 的取值范围是
的取值范围是 ![]() 。
。
15、已知数列![]() 满足:
满足:![]() ,则使
,则使![]() 成立的n的值是 21 。
成立的n的值是 21 。
16、等差数列![]() 的前n项和为Sn,且
的前n项和为Sn,且![]() 如果存在正整数M,使得对一切
如果存在正整数M,使得对一切![]() ,
,![]() 都成立,则M的最小值是 2 。
都成立,则M的最小值是 2 。
三、解答题(共86分)
17、(本题12分)设![]() 所有项的系数和为
所有项的系数和为![]() ,求
,求![]() 的值。 解:
的值。 解:![]()
![]() ,令
,令![]() ,得
,得
![]() , ∴
, ∴![]() =
=![]()
18、(本题12分)已知![]() 的展开式的第7项是
的展开式的第7项是![]() ,判断函数
,判断函数![]() 的奇偶性。
的奇偶性。
解: ![]() ,
,![]()
![]() , 易知,
, 易知, ![]() 是奇函数.
是奇函数.
19、(本题14分)已知![]() 成等差数列,
成等差数列,![]() 成等比数列,且
成等比数列,且![]() =15,
=15,![]() =14,
=14,![]() =15,
=15,![]() =20.求等差数列
=20.求等差数列![]() 的公差d及等比数列
的公差d及等比数列![]() 的公比q。
的公比q。
解: ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() , 显见,
, 显见, ![]()
则
![]() , 得
, 得![]() ,
,![]()
∴![]() ,
, ![]()
20、(本题14分)已知![]() 是定义在
是定义在![]() 上的奇函数,且在定义域上递减,若
上的奇函数,且在定义域上递减,若![]() 成立,求实数
成立,求实数![]() 的取值范围。
的取值范围。
解: ∵![]() 是定义在
是定义在![]() 上的奇函数, ∴
上的奇函数, ∴![]()
又∵![]() 在定义域上递减, ∴
在定义域上递减, ∴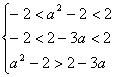 , 即
, 即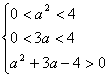 ∴
∴![]()
21、(本题16分)已知:![]()
(1)求![]() 的值;(2)讨论
的值;(2)讨论![]() 的单调性;(3)解不等式
的单调性;(3)解不等式![]() 。
。
解:(1)![]()
(2)定义域 ![]() ,设
,设![]() ,
,
∵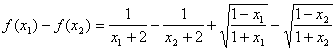
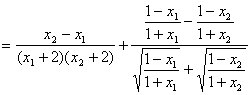
![]()
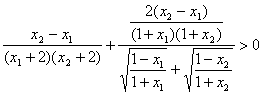
∴![]() ,即
,即![]() 在其定义域上是减函数。
在其定义域上是减函数。
(3)![]() ,即
,即![]()
![]() ,∵
,∵![]() 在其定义域上是减函数
在其定义域上是减函数
∴![]() ,又∵
,又∵![]() 的定义域为
的定义域为![]() ,∴
,∴![]()
∴不等式![]() 的解集是
的解集是 ![]() 。
。
22、(本题18分)如右图是在竖直平面内的一个“通道游戏”,图中竖直线段和斜线段都表示通道,并且在交点处相通,若竖直线段有一条的为第一层,有二条的为第二层,依次类推,现有一颗小弹子从第1层的通道里向下运动。求:
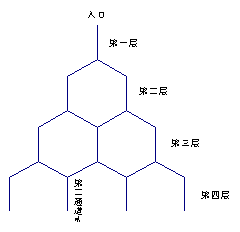 (1)该小弹子落入第4层第2个竖直通道
(1)该小弹子落入第4层第2个竖直通道
的概率(从左向右数);
(2)猜想落入第n+1层的第m个通道里的概率。
(3)该小弹子落入第![]() 层第
层第![]() 个竖直通道的
个竖直通道的
路径数与该小弹子落入第![]() 层第
层第![]() 个竖直通
个竖直通
道的路径数之和等于什么?
[假设在交点处小弹子向左或向右是等可能的].
解:(1)∵在交点处小弹子向左或向右是等可能的,∴小弹子落入第4层第1个竖直通道的路径只有1条,落入第4层第2个竖直通道的路径有3条,第3个有3条,第4个有1条,∴所求概率P= ![]() =
=![]()
(2)利用杨辉三角的特点可猜想,所求的概率P=![]() =
=![]()
![]()
(3)![]() ,即该小弹子落入第
,即该小弹子落入第![]() 层第
层第![]() 个竖直通道的路径数与该小弹子落入第
个竖直通道的路径数与该小弹子落入第![]() 层第
层第![]() 个竖直通道的路径数之和等于该小弹子落入第
个竖直通道的路径数之和等于该小弹子落入第![]() 层第
层第![]() 个竖直通道的路径数。
个竖直通道的路径数。