高考数学模拟试卷9答案

高考数学模拟试卷9

参考答案及评分标准

一、选择题：

（1）C　　 （2）C　　 （3）C　　 （4）D　　 （5）C　　 （6）A　　

（7）B　　 （8）C　　 （9）A　　（10）D　　（11）B　　（12）B

二、填空题：

（13）分层

（14）x= —1或3x—4y+3=0

（15）⑤

（16）　

三、解答题

（17）基本事件的种数为=15种　　　　　　　  　　　　　　　　 ……（2分）

（Ⅰ）恰有一名参赛学生是男生的基本事件有=9种　　　　  　……（4分）

这一事件的概率P₁==0.6　　　　　　　　　　　　　　　　　  ……（5分）

（Ⅱ）至少有一名参赛学生是男生这一事件是由两类事件构成的，即恰有一名参赛学生是男生和两名参赛学生都是男生

所求事件的概率P₂=　　　　　　　　　　　  　 ……（9分）

（Ⅲ）至多有一名参赛学生是男生这一事件也是由两类事件构成的，即参赛学生没有男生和恰有一名参赛学生是男生

所求事件的概率P₃=　　　　　　　　　　　  　……（12分）

（18）（Ⅰ）=coscos+sin (—sin)=cos(+)=cos2x …（3分）

=(cos+cos,sin—sin)　　　　　　　　　　　　　 ……（4分）

∴

= … （5分）

∵x∈[，]　　,　　　　　　  ∴=—2cosx 　　　　　　……（6分）

（Ⅱ）f(x)＝—=cos2x—(—2cosx)=cos2x+2cosx

=2cos²x+2cosx—1=　　　　　　　　　　　　　 …… （10分）

∵x∈[，]　,　　　　　　　　 

∴—1≤cosx≤0

∴当cosx=—时，f(x)_min=　　　　　　　　　　　　　　　　  ……（12分）

（19）（Ⅰ）由f(x)=ax²+bx+c 知：f′(x)=2ax+b　　　　　　　　　  ……（2分）

由已知得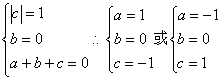：　　　　　　　　 　　……（4分）

∵a>0　　　　　　　　　　　　　 ∴f(x)=x²—1　　　　　　　　   ……（5分）

（Ⅱ）x₁,x₂∈[0,1]且x₁≠x₂

∴f(x₂) — f(x₁)=(x₂²—1) —(x₁²—1)=x₂²—x₁²

∴f(x₂) —f(x₁)=x₂²—x₁²=x₂+x₁·x₂—x₁　　　　　　　　　　  ……（7分）

∵x₁,x₂∈[0,1]　　 ,　　　　　　　　　 ∴0≤x₂+x₁≤2

∴x₂+x₁·x₂—x₁≤2x₂—x₁ 即 f(x₂) — f(x₁)≤2x₂—x₁成立。 ……（9分）

又 f(x₂) — f(x₁)= x₂²—x₁²

∵x₁,x₂∈[0,1]　 ,　　　　　　　　　　 ∴x₁²，x₂²∈[0，1]

∴—1≤x₂²—x₁²≤1　　,　　　　　　　　　 ∴ x₂²—x₁²≤1

∴f(x₂) — f(x₁)= x₂²—x₁²≤1成立。　　　　　　　　　　　　 ……（12分）

由以上知：f(x₂) — f(x₁)≤2x₂—x₁与f(x₂) —f(x₁)≤1都成立。

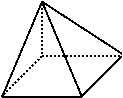
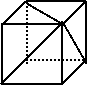
（20）（Ⅰ）有一条侧棱垂直于底面的四棱锥　　　　　　　　　　　  ……（1分）

　　　　　　　　　　　　　　　　 ……（3分）

（Ⅱ）需要3个这样的几何体　　　　　　　　　　　　　　　　　　 ……（5分）

（Ⅲ）①取DD₁中点F，连AF，则AF∥BE。

∴∠FAB₁为异面直线EB与AB₁所成的角。　　　　　　　　　　　　　 ……（6分）

易计算得 B₁F=9，AF=3 ，AB₁=6

∴cos∠FAB₁=

∴异面直线EB与AB₁所成角的余弦值为　　　　　　　　　　　  ……（8分）

②设B₁E、BC的延长线交于点G，连结GA，则GA为平面AB₁E与平面ABC所成二面角的棱　　　　　　　　　　　　　　　 　　　　　　　　　　　　　 ……（9分）

在底面ABC内作BH⊥AG，垂足为H.连结HB₁，由三垂线定理知：B₁H⊥AG，

∴∠B₁HB为平面AB₁E与平面ABC所成二面角的平面角。　　　　　　  ……（10分）

在Rt△ABG中，BH=

∴HB₁=

∴cos∠B₁HB=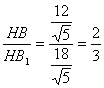

∴平面AB₁E与平面ABC所成二面角的余弦值为。　　　　　　　　 ……（12分）

（21）（Ⅰ）由y＝得　 ，　　　∴

∵x<—2　 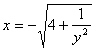，　　　　 ∴　　　　　　　　　　　　  ……（2分）

∴g(x)= 　 （x>0）　　　　  　　　　　　　　　　　　……（3分）

（II）∵点An(a_n,)在曲线y＝g(x)上(n∈N₊)

∴= g(a_n)= 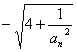　,　并且a_n >0　　　　　　　　　　  ……（4分）

　，　

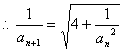∴数列{}为等差数列。　　　　　　　　　　　　　　　　　　  ……（6分）

（Ⅲ）∵数列{}为等差数列，并且首项为=1，公差为4

∴=1+4（n—1）　　，　　　　 ∴

∵a_n >0　　 ，　　　　　　　　 ∴　　　　　　　　  ……（9分）

（Ⅳ）b_n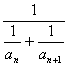＝=,　　……（11分）

∴S_n＝b₁＋b₂+…＋b_n=

=　　　　　　　　　　　　　　　　　　　　　　　　 ……（12分）

（22）（Ⅰ）圆F₁：（x+3）²+y²=5　，　　圆F₂：（x—3）²+ y²=45　　　 ……（1分）

设动圆半径为r，圆心为M，则由已知得：

 

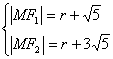
∴MF₂—MF₁=2　　　　　　　　　　　　　　　　　　　　　  ……（2分）

∴动圆圆心的轨迹C为以F₁，F₂为焦点，实轴长为2的双曲线的左支，

易得其方程为：（x<0） 　　　　　　　　　　　　　　 ……（4分）

（Ⅱ）设L方程为：y+16=k（x+20），并设L与轨迹C交点坐标为（x₁，y₁），

（x₂，y₂）.则由已知得：,　即x₁+x₂= —40……①

由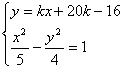　　 消去y得：

（4—5k²）x²—10k（20k—16）x—5（20k—16）²—20=0

∴x₁+x₂=　　……②　　　　　　　　  　　　　　　　……（6分）

由①、②得：= —40

∴k=1

∴所求直线L的方程为y=x+4　　　　　　　　　　　　　　　　　　  ……（8分）

（Ⅲ）　　　　 y

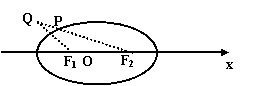椭圆的长轴长等于PF₁+PF₂.

要长轴最短，只需在直线L上找一点P，使点P到F₁、F₂的距离之和最小。

由平面几何知识知：作F₁关于L的对称点Q，连结QF₂交直线L于点P，则点P即为所求点，坐标为（）　　　　　　　　　　　　　　　　　  ……（11分）

此时长轴2a=PF₁+PF₂=PQ+PF₂=QF₂=5

从而a²=，C=3

∴b²=a²—c²=

∴椭圆C′的方程为：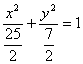

　　　　　　　　　  　　　　　　　　　　　　　　　　　　　　　……（14分）