高考数学模拟试题7
第Ⅰ卷(选择题 共60分 )
一、 选择题:本大题共12小题,每小题5分,共60分;在每小题给出的四个选项中,只有一项是符合题目要求的。
1.非空集合A,B存在关系A![]() B,I是全集,下列集合为空集的是
( )
B,I是全集,下列集合为空集的是
( )
A. A![]() B B.
B B.
![]() C.
C.![]() D.
D.![]()
2.一个长方体共一个顶点的三个面的面积分别为12,15,20,则长方体的对角线长为
A.![]() B.
B.![]() C.6 D.8( )
C.6 D.8( )
3. 已知数列![]() 它的前n项的积大于105,则正整数n 的最小值
它的前n项的积大于105,则正整数n 的最小值
是 ( )
A.12 B.11 C.10 D.8
4.已知![]() 如果
如果![]() ,则m的值为
( )
,则m的值为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5. 函数![]() 在同一单调区间内的
在同一单调区间内的![]() 处取最大值
处取最大值![]() ,在
,在![]() 处取最小值
处取最小值![]() ,则函数的解析式为 ( ) A.
,则函数的解析式为 ( ) A.![]() B.
B. ![]()
C.![]() D.
D.![]()
6.已知过球面上三点A、B、C的截面与球心的距离等于球的半径的一半,若AB=BC=AC=2,则球的体积为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7. 从6名志愿者中选出4人分别从事翻译、导游、导购、保洁四种工作,甲、乙两名志愿者都不从事翻译工作,则选派方案共有 ( )
A.280 B.240 C.180 D.96
8.函数y=cos x , x∈[0, π]的图像与直线x=0, y= - 1所组成的封闭图形,绕x轴旋转一周所得的几何体的体积为 ( )
A.π3 B.π C.0.5π3 D.0.5π2
9.在100件产品中,有60件正品,40件次品,从中有放回地抽取3次,每次抽取1件,那么恰有2次抽到正品的概率是 ( )
A.0.024 B.0.144 C.0.236 D.0.432
10.已知复数z满足arg (3z -![]() )=
)=![]() , ôz+1ô=
, ôz+1ô=![]() , 则arg z
= (
)
, 则arg z
= (
)
A.argtan2 B.π-
argtan2 C.π- argtan![]() D.argtan
D.argtan![]()
11.直线l:x+2y-3=0与圆C:x2+y2+x-6y+m=0有两个交点A、B,O为坐标原点,若![]() , 则m的值是
( )
, 则m的值是
( )
A.2
B.3
C.-1
D.![]()
12.李老师从银行贷款1万元用于购买电脑,贷款月利率为1%,按复利计算(即本月利息计入下月本金),若从贷款后次月初开始归还,分10个月等额分期付款,10次还清,每次应还(精确到1元) ( )
A.1056元 B.1100元 C.1105元 D.1167元
第Ⅱ卷(选择题 共90分)
二、 填空题:本大题共4个小题,每小题4分,满分16分。
13.求值:![]() =
=
14.一个袋子里装有大小相同的3个红球和2个黄球,从中同时取出2个,则其中含红球个数的数学期望是 (用数字作答)
15. 已知二项式
(1+2x) n 的展开式中各项系数之和为a n ,其二项式系数和为b n , 则![]() 的值是
。
的值是
。
16.有下列命题:① ![]() 成等比数列的充分但非必要条件; ②
若角
成等比数列的充分但非必要条件; ②
若角![]() 满足
满足![]() 则
则![]() ; ③ 若不等式
; ③ 若不等式
![]() 的解集非空,则必有
的解集非空,则必有![]() ④ 函数
④ 函数![]() 的值域是[-2,2]。其中错误的命题的序号是
(把错误的命题的序号都填上)
的值域是[-2,2]。其中错误的命题的序号是
(把错误的命题的序号都填上)
三、解答题:本大题共6个小题,共74分;解答应写出文字说明、演算步骤。
17.(本小题满分12分)
已知函数![]() 和定义在R上的奇函数
和定义在R上的奇函数![]() ,当
,当![]() ,有
,有![]() 求
求![]() 的反函数。
的反函数。
18.(本小题满分12分)
某人有5把钥匙,其中只有1把能打开房门,但忘记了是哪一把,只好逐把试开,求下列各事件的概率:
(1)第一次就打开房门;
(2)前三次打开房门.
19.(本小题满分12分)
如图,已知三棱柱![]() 的底面是边长为2的正三角形,侧棱
的底面是边长为2的正三角形,侧棱![]() 与AB,AC均成45°角,且
与AB,AC均成45°角,且![]() 于E,
于E,![]() 于F.
于F.
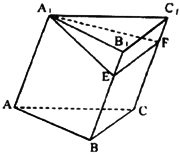 (I) 求证:平面
(I) 求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求点A到平面![]() 的距离;
的距离;
(Ⅲ)当![]() 多长时,点
多长时,点![]() 到平面ABC与平面
到平面ABC与平面![]() 的距离相等?
的距离相等?
20.(本小题满分12分)
随着机构改革工作的深入进行,各单位要减员增效,有一家公司现有职员![]() 人(140<
人(140<![]() <420,且
<420,且![]() 为偶数),每人每年可创利
为偶数),每人每年可创利![]() 万元.据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利
万元.据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利![]() 万元,但公司需付下岗职员每人每年
万元,但公司需付下岗职员每人每年![]() 万元的生活费,并且该公司正常运转所需人数不得小于现有职员的
万元的生活费,并且该公司正常运转所需人数不得小于现有职员的![]() ,为获得最大的经济效益,该公司应裁员多少人?
,为获得最大的经济效益,该公司应裁员多少人?
21.(本小题满分12分)
已知![]() 且
且![]() 、
、![]() 、
、 ![]() ……
……![]() 组成等差数列(n为正偶数),又
组成等差数列(n为正偶数),又![]() ,
,![]() 。
。
①求数列的通项![]() ;
;
②比较![]() 与3的大小;
与3的大小;
③求![]() 的单调区间和极值。
的单调区间和极值。
22.(本小题满分14分)
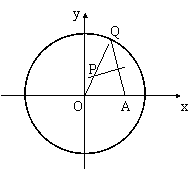 已知圆C:x2 +
y2 = 4, A(
已知圆C:x2 +
y2 = 4, A(![]() , 0)是圆内一点。Q是圆上一动点,AQ的垂直平分线交OQ于P,当点Q在圆C上运动一周时,点P的轨迹为曲线E,
, 0)是圆内一点。Q是圆上一动点,AQ的垂直平分线交OQ于P,当点Q在圆C上运动一周时,点P的轨迹为曲线E,
(Ⅰ)求曲线E的方程;
(Ⅱ)过点O作倾斜角为θ的直线与曲线E
交于B1、B2两点,当θ在范围![]() 内变化时,
内变化时,
求ΔAB1B2的面积S(θ) 的最大值。
高考数学模拟试题7答案
一、选择题:本大题共12小题;每小题5分,共60分.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | B | B | C | A | B | B | C | B | D | D | C |
二、填空题:本大题共4小题;每小题4分,共16分.
(13)4 (14)1.2 (15)1 (16)③
三、解答题:本大题共6小题;共74分.
17. 解:∵![]() 是
是![]() 上的奇函数
上的奇函数
∴![]() ……………………………………………………………………2分
……………………………………………………………………2分
当![]() 时,有
时,有![]() ,则
,则
![]() ………………………………………………6分
………………………………………………6分
∴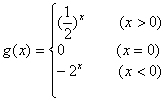 …………………………………………………8分
…………………………………………………8分
分别求各段上的反函数,得
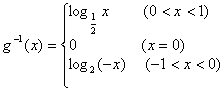 .………………………………………12分
.………………………………………12分
18.解:
设{第k次打开}=AK(k=1,2,3,4,5)
(1)P(A1)=![]() ……………………………………………………………4分
……………………………………………………………4分
(2)设{前三次打开}=A,则A=A1+![]() A2+
A2+![]()
![]() A3………………6分
A3………………6分
A1,![]() , A2,
, A2,![]() ,A3彼此相互独立,A1,
,A3彼此相互独立,A1,![]() A2,
A2,![]()
![]() A3彼此互斥,故 P(A)=P(A1+
A3彼此互斥,故 P(A)=P(A1+![]() A2+
A2+![]()
![]() A3)
A3)
=P(A1)+P(![]() )P(
)P(![]() )+P(
)+P(![]() )P(
)P(![]() )P(A3)……8分
)P(A3)……8分
=![]() ………………………………………12分
………………………………………12分
|
∵![]() ∥
∥![]() ,∴
,∴![]() ……………………1分
……………………1分
又![]() .∴
.∴![]() 所以,平面
所以,平面
![]() ………………………………3分
………………………………3分
(Ⅱ)因为![]() ,
,
又![]() ∴
∴![]() ≌
≌![]() ,∴
,∴![]()
∴![]()
![]()
![]() ,∴EF=
,∴EF=![]() ∴
∴![]()
∴![]() 为等腰直角三角形……………………………………………5分
为等腰直角三角形……………………………………………5分
取EF的中点N,连![]() ,则
,则![]() ,
,
所以![]() ……………………………………………6分
……………………………………………6分
所以![]() 为点
为点![]() 到平面
到平面![]() 的距离。
的距离。
又![]() ,所以点
,所以点![]() 到平面
到平面![]() 的距离为1. …………………8分
的距离为1. …………………8分
(Ⅲ)设BC,![]() 的中点分别为D,
的中点分别为D,![]() 连AD,
连AD,![]() 和
和![]() ,则N∈
,则N∈![]()
∵![]() ∥
∥![]() ∥
∥![]() ,∴A,
,∴A,![]() ,D,
,D,![]() 四点共面,∴AD∥
四点共面,∴AD∥![]()
∴![]() 为平行四边形, ……………………………………………………9分
为平行四边形, ……………………………………………………9分
∵![]() ∴
∴![]()
∴![]() ∴
∴![]()
∴![]() ………………………………………………10分
………………………………………………10分
作![]() ,
,
若![]() ,
,
则![]() ≌
≌![]() ,于是
,于是![]()
即当![]() 时,点
时,点![]() 到平面ABC和平面
到平面ABC和平面![]() 的距离相等.……………12分
的距离相等.……………12分
20.解:设裁员![]() 人,可获得的经济效益为
人,可获得的经济效益为![]() 万元,则
万元,则
![]() ………………………………………………3分
………………………………………………3分
=![]() ……………………………………………5分
……………………………………………5分
![]() 令
令![]() ,得
,得![]()
依题意 ![]() ≥
≥![]() ∴0<
∴0<![]() ≤
≤![]() 又140<
又140<![]() <420 ∴70<
<420 ∴70<![]() <210
<210
(1)当0<![]() ≤
≤![]() ,即70<
,即70<![]() ≤140时
≤140时
![]()
![]() 取到最大值…………………………………………………8分
取到最大值…………………………………………………8分
(2)当![]() >
>![]() ,即140<
,即140<![]() <210时
<210时
![]()
![]() 取到最大值…………………………………………………10分
取到最大值…………………………………………………10分
综上所述,当70<![]() ≤140时,应裁员
≤140时,应裁员![]() 人;
人;
当140<![]() <210时,应裁员
<210时,应裁员![]() 人.……………………………12分
人.……………………………12分
21. 解:(1)![]()
![]() …………………………………………………1分
…………………………………………………1分
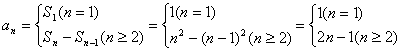 ……..3分
……..3分
![]() ,
,
![]() ………………………………………4分
………………………………………4分
(2)
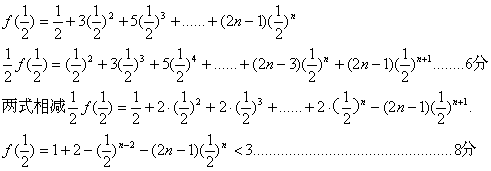 (3)
(3)
n=3时 ![]() ………9分
………9分
令![]()
| ( | -1 |
|
| ( | |
|
| + | 0 | - | 0 | + |
|
|
|
|
|
|
|
单增区间是![]()
单减区间是[-1,-15] ………………………………………………………… 11分
极大值为![]() , 极小值为
, 极小值为![]() …………………………………………………12分
…………………………………………………12分![]()
22. 解:(Ⅰ)∵P在AQ的垂直平分线上,又在半径OQ上,
∴ ∣PQ∣=∣PA∣且∣OP∣+∣PA∣=∣OQ∣=2,……………………2分
故P点的轨迹是以O、A为焦点,长轴长为2,中心在(![]() ,0)的椭圆:
,0)的椭圆:
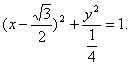 ……………………………………………………4分
……………………………………………………4分
(Ⅱ)法一:设∣OB1∣=x,则∣AB1∣=2–x,在ΔOAB1中,由余弦定理得
∣AB1∣2 =∣OB1∣2+∣OA∣2 - 2∣OB1∣•∣OA∣cosθ,……………………6分
(2-x)2=x2+3-2![]() x•cosθ,
x•cosθ,
解得 ![]() ,……………………………………………………7分
,……………………………………………………7分
同理可得
![]() .
…………………………………………………8分
.
…………………………………………………8分
S(θ) = ![]()
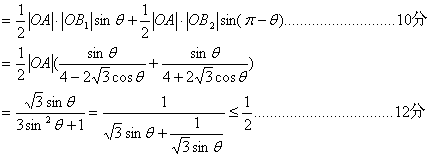
当且仅当![]()
∴![]() …………………………………………14分
…………………………………………14分
法二:设过点O倾斜角为![]() 的直线方程为
的直线方程为![]() 。
。
由已知列方程组: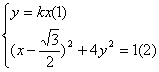 将(1)带入(2)化简得:
将(1)带入(2)化简得:
![]()
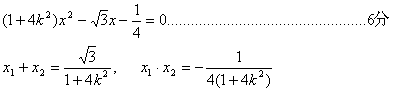
![]()
![]()
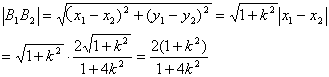 ……………..8分
……………..8分
S(θ) = ![]()
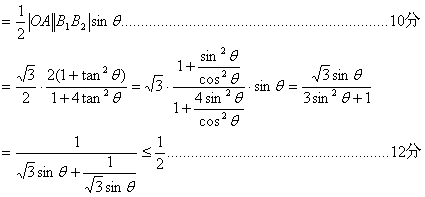
当且仅当![]()
∴![]() …………………………………………14分
…………………………………………14分