高考数学模拟试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间120分钟.
第Ⅰ卷(选择题共60分)
一、选择题:本大题共12小题,每小题5分,共60分.
1.集合![]()
A.{(1,0)} B.{y0≤y≤1} C.{1,0} D.φ ( )
2.已知复数![]() ( )
( )
A.2 B.4 C.8 D.16
3.正方体ABCD—A1B1C1D1,E,F分别是正方形A1B1C1D1和
ADD1A1的中心,则EF和CD所成的角是
( )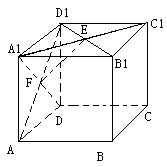
A.60° B.45°
C.30° D.90°
4.已知![]()
A.![]() B.
B.![]() ( )
( )
C.![]() D.不确定
D.不确定
5.在(0,2![]() )内使
)内使![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() ( )
( )
C.![]() D.
D.![]()
6.不等式![]() 的解集是
( )
的解集是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.下列四个函数中,值域是![]() 的一个函数是
( )
的一个函数是
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.设![]() 为正常数,
为正常数,![]() 为奇函数的( )
为奇函数的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分又不必要条件
9.设双曲线![]() 中,离心率
中,离心率![]() ,则两条渐近线的夹角
,则两条渐近线的夹角
θ的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.一张报纸,其厚度为a,面积为b,现将此报纸对折(既沿对边中点的连线折叠)7次,
这时报纸的厚度和面积分别是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.对某种产品的6件不同正品和4件不同次品,一一进行测试,到区分出所有次品为止。
若所有次品恰好在第五次测试被全部发现,则这样的测试方法有 ( )
A.24种 B.96种
C.576种 D.720种
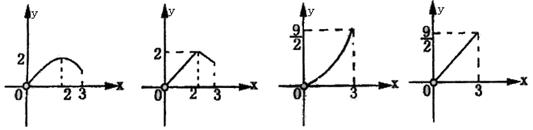
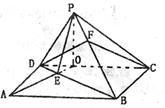
12.三棱锥P—ABC的高PO=8,AC=BC=3,∠ACB=30°,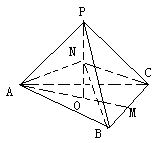
M,N分别在BC和PO上,且CM=x,PN=2CM,
试问下面的四个图象中哪个图象大致描绘了三棱锥
N—AMC的体积V与x的变化关系![]()
|
|
第Ⅱ卷(非选择题共90分)
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
13.已知![]() 展开式的第四项的值等于106,则x=
展开式的第四项的值等于106,则x=
14.过抛物线![]() 焦点的直线交抛物线于A、B两点,已知AB=8,O为坐标原点,则
焦点的直线交抛物线于A、B两点,已知AB=8,O为坐标原点,则
△OAB的重心的横坐标为
15.![]() 的值为
的值为
16.对于函数![]() ,给出下列四个命题:
,给出下列四个命题:
①存在![]() ;
;
②存在![]() 恒成立;
恒成立;
③存在![]() ,使函数
,使函数![]() 的图像关于y轴对称;
的图像关于y轴对称;
④函数![]() 的图象关于点
的图象关于点![]() 对称;
对称;
其中正确命题的序号是
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)
若![]() ,解关于x的不等式
,解关于x的不等式![]() .
.
18.(本小题满分12分)
已知△ABC中,A、B、C分别是三个内角,a、b、c分别是角A、B、C的对边,已知![]() 的外接圆的半径为
的外接圆的半径为![]() .
.
(Ⅰ)求角C (Ⅱ)求△ABC面积S的最大值.
19.(本小题满分12分)
矩形ABCD中,AB=6,BC=![]() ,沿对角线BD将三角形ABD向上折起,使点A移至点P,使点P在平面BCD上的射影O在DC上,(如图).
,沿对角线BD将三角形ABD向上折起,使点A移至点P,使点P在平面BCD上的射影O在DC上,(如图).
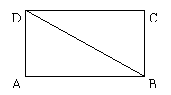 (Ⅰ)求证:PD⊥PC;
(Ⅰ)求证:PD⊥PC;
(Ⅱ)(理科)求二面角P—DB—C的大小;
(文科)求二面角P—DB—C的余弦值;
(Ⅲ)求直线CD与平面PBD所成角的大小.
20.(本小题满分12分)
已知抛物线![]() 的弦AB与直线
的弦AB与直线![]() 有公共点,且弦AB的中点N到y轴的距离为
有公共点,且弦AB的中点N到y轴的距离为
1,求弦AB长度的最大值,并求此时直线AB所在的直线的方程.
 |
21.(本小题满分12分)
某农产品去年各季度的市场价格如下表:
| 季 度 | 第一季度 | 第二季度 | 第三季度 | 第四季度 |
| 每吨售价 (单位:元) | 195.5 | 200.5 | 204.5 | 199.5 |
今年某公司计划按去年各季度市场价格的“平衡价m”(平衡价m是这样的一个量:与上年各季度售价差比较,m与各季度售价差的平方和最小)收购该种农产品,并按每100元纳税10元(又称征税率为10个百分点),计划可收购a万吨,政府为了鼓励收购公司多收购这种农产品,决定将税率降低x个百分点,预测收购量可增加2x个百分点.
(Ⅰ)根据题中条件填空,m= (元/吨)
(Ⅱ)写出税收y(万元)与x的函数关系式;
(Ⅲ)若要使此项税收在税率调节后不少于原计划税收的83.2%,试确定x的取值范围.
22.(本小题满分14分)
已知二次函数![]() 的图象的顶点坐标是
的图象的顶点坐标是![]()
(Ⅰ)求![]() 的表达式,并求出f(1)、f(2)的值;
的表达式,并求出f(1)、f(2)的值;
(Ⅱ)数列{an},{bn},若对任意的实数x都满足![]() ,
,
其中![]() 是定义在实数R上的一个函数,求数列{an},{bn}的通项公式;
是定义在实数R上的一个函数,求数列{an},{bn}的通项公式;
(Ⅲ)设圆![]() ,若圆Cn与圆Cn+1外切,{rn}是各项都是正
,若圆Cn与圆Cn+1外切,{rn}是各项都是正
数的等比数列,记Sn是前n个圆的面积之和,求![]() .
.
高考数学模拟试题
参考答案
一、选择题:每小题5分,满分60分.
1.A 2.B 3.B 4.B 5.A 6.B 7.D 8.A 9.B 10.C 11.C 12.A
二、填空题:每小题4分,满分16分.
13.![]() ; 14.2; 15.2; 16.①③④
; 14.2; 15.2; 16.①③④
三、解答题:
7.解:原不等式可化为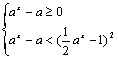 即
即![]() ……………4分
……………4分
当a>3时,![]() ………7分 当a=3时,且
………7分 当a=3时,且![]() ……………11分
……………11分
∴当a=3时,原不等式的解集{![]() };当a>3时,{
};当a>3时,{![]() }……12分
}……12分
18.解:(I)![]() ,由正弦定理得:
,由正弦定理得:
![]() ……………3分
……………3分
由余弦定理得:![]() ………6分
………6分
(II)![]()
![]() ……………………………………………………9分
……………………………………………………9分
![]() ,
,
![]() ………………………………………………………………12分
………………………………………………………………12分
法2:![]() ……4分
……4分
![]()
=![]()
![]()
![]() …………………………………10分
…………………………………10分
当![]() ………………………………………12分
………………………………………12分
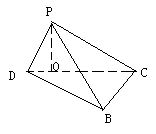
19.解:(I)∵PO⊥平面BCD,∴PO⊥BC ∴平面PCD⊥平面BCD又 ∵BC⊥CD
|
DP⊥CP……(理3分,文4分)
(II)作OE⊥BD于E,则PE⊥BD,则AE⊥BD,A、E、O共线
∴∠PEO就是二面角P—BD—C的平面角.在Rt△ABD中
AB=6,AD=![]() ∴∠ABD=30°,∠ADB=60°,
∴∠ABD=30°,∠ADB=60°,
则∠DAE=30° ∴AE=ADcos60°=3=PE,
![]() ∴OE=1 在Rt△POE中,
∴OE=1 在Rt△POE中,![]()
∴∠PEO=![]() ………………………………………(理科8分,文科12分)
………………………………………(理科8分,文科12分)
(III)作CF⊥PB,F为垂足,∴DP⊥平面PCB ∴平面PBD⊥平面BCP
∵CF⊥平面PDB,∠CDF就是CD与平面BDP所成的角在Rt△PBC中,
∴∠BCP=90°,BC=2![]() ,BP=6 ∴PC=2
,BP=6 ∴PC=2![]() ∴CF·BP=BC·CP,∴CF=2
∴CF·BP=BC·CP,∴CF=2![]()
在Rt△CDF中,sin∠CDF=![]() ………………(理12分)
………………(理12分)
20.解:设![]() 、
、![]() ,中点N(1,y0).
,中点N(1,y0).
当AB直线的倾斜角90°时,AB直线方程是x=1,AB=2.………………2分
当AB直线的倾斜角不为90°时,![]()
相减得:![]() ……………4分
……………4分
设AB直线方程为:![]() 由于弦AB与直线y=1有公
由于弦AB与直线y=1有公
共点,故当 ………………………6分
………………………6分
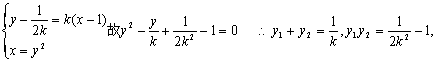
故AB=![]() ……8分
……8分
![]()
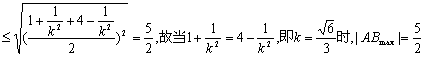 ………10分
………10分
此时AB直线方程是:![]() ……………………………………12分
……………………………………12分
21.解:(I)200;…………………………………………………………………………3分
(II)降低税率后的税率为(10-x)%,农产品的收购量为a(1+2x%)万担,收购总金额为200a(1+2x%)故y=200a(1+2x%)(10-x)%=![]()
![]() ……………………………………………7分
……………………………………………7分
(III)原计划税收为200a×10%=20a(万元),依题意得:![]()
![]()
答:x的取值范围是0<x≤2.
22.解:(I)由已知得![]()
![]()
![]() …………………………4分
…………………………4分
(II)![]() ①
①
![]() ②
②
由①②得![]() …………………………………………8分
…………………………………………8分
(III)![]() ,设数列{rn}的公比为q,则
,设数列{rn}的公比为q,则![]()
![]()
![]() ………10分
………10分
![]()
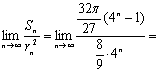
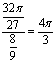 ……………………………………………14分
……………………………………………14分