高三第二学期期末适应性练习
数 学
学校____________ 班级____________ 姓名____________
参考公式：
三角函数的和差化积公式：
一、选择题：本大题共10个小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的。
（1）已知 
，那么复数z在复平面对的点位于（ ）
（A）第一象限 （B）第二象限
（C）第三象限 （D）第四象限
（2）已知函数y=f（x）是定义在[a,b]上的减函数，那么
是（ ）
（A）在[f(a),f(b)]上的增函数 （B）在[f(b),f(a)]上的增函数
（C）在[f(a),f(b)]上的减函数 （D）在[f(b),f(a)]上的减函数
（3）椭圆
上的一点M到左焦点
的距离为2，N是
的中点，则ON等于（ ）
（A）2 （B）4
（C）8
（D）
（4）条件“0<x<5”是条件“x-2<3”的（ ）
（A）充分但非必要条件 （B）必要但非充分条件
（C）充要条件 （D）既非充分又非必要条件
（5）（理科）直线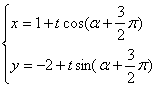
（其中t为参数，
）的倾斜角为（ ）
（A）α
（B）
（C）
（D）
（文科）直线3x+4y-7=0与直线6x+8y+3=0之间的距离是（ ）
（A）
（B）2
（C）
（D）
（6）已知x，y为正实数，且x，
，
，y成等差数列，x，
，
，y成等比数列，那么
的取值范围是（ ）
（A）（0，+∞） （B）（0，4]
（C）[4，+∞） （D）[2，4]
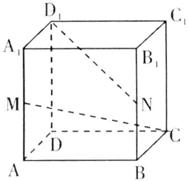
（7）正方体
中，若M、N分别为
和
的中点，则异面直线CM与
所成角的余弦值为（ ）
（A）
（B）
（C）
（D）
（8）设α，β是锐角三角形的两个互不相等的内角，若x=sin(α+β)，y=cosα+cosβ，
z=sinα+sinβ，则x，y，z之间的大小关系是（ ）
（A）x<y<z （B）x>y>z
（C）x<z<y （D）y<x<z
（9）在下列命题中
①直线a∥直线b，直线b∥平面α，则a∥α
②若平面α⊥平面γ，平面β⊥平面γ，则α∥β
③若平面α内不共线的三点到平面β的距离相等，则α∥β
④若E、F、G、H分别为空间四边形ABCD的AB、BC、CD、DA的中点，
则∠FEH=90°
其中正确命题的个数为（ ）
（A）3 （B）2
（C）1 （D）0
（10）集合M={-2，0，1}，N={1，2，3，4，5}，映射f：M→N，使任意x∈M，都有x+f(x)+xf(x)是奇数，则这样的映射共有（ ）
（A）60个 （B）45个
（C）27个 （D）11个
二、填空题：本大题共4小题，每小题4分，共16分。把答案填在题中横线上。
（11）棱长分别为3、4、5的长方体内接于球O，则球O的表面积为_____________。
（12）已知双曲线的两条渐近线方程分别为3x-4y-2=0与3x+4y-10=0，其顶点为（2，4）与（2，-2），则这个双曲线的方程是_____________。
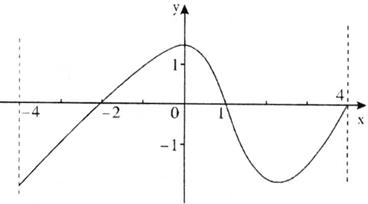
（13）设函数f(x)的定义域为[-4，4]，其图像如图。
那么不等式
的解集为_____________。
（14）某篮球队12名队员年龄各不相同，欲将他们分成两个队比赛，使得一个队5人中年龄最小的比另一队5人中年龄最大的还大，另2人在场下休息。那么共有分队方法的种数为_____________。
三、解答题：本大题共6个小题，共84分。解答应写出文字说明、证明过程或演算步骤。
（15）（本小题满分14分）
解关于x 的不等式：
其中a>0，且a≠1。
（16）（本小题满分14分）
已知函数
的最大值为
，其最小正周期为π。
（Ⅰ）求实数a与ω的值。
（Ⅱ）写出曲线y=f(x)的对称轴方程及其对称中心的坐标。
（17）（本小题满分14分）
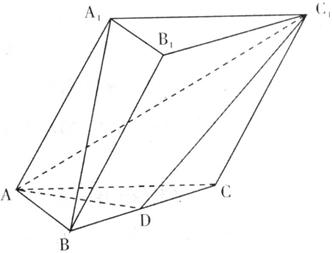
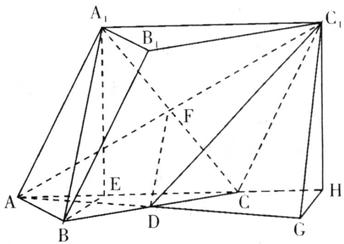
已知斜三棱柱
各棱长都等于a，侧面
⊥底面ABC，其侧棱与底面所成的角为60°，且D是BD的中点。
（Ⅰ）求证：
；
（Ⅱ）求证：
∥截面
；
（Ⅲ）求二面角
的正切值
（18）（本小题满分12分）
某粒子在回旋加速器中作圆周运动。已知出发t个单位时间通过的路程为
（a，b是常数）。如果最初转完第一圈时用了5个单位时间，接下去又用了3个单位时间转完第2圈。
（Ⅰ）问：该粒子再用多少单位时间可以转完第3圈？
（Ⅱ）试问从第几圈开始，粒子转完一圈的时间不超过1个单位时间？
（19）（本小题满分14分）
设定义在（0，+∞）上的函数f(x)满足：
（1）对于任意实数a、b，都有f(a·b)=f(a)+f(b)-p，其中p是正实常数；
（2）f(2)= p-1；
（3）当x>1时，总有f(x)< p。
（Ⅰ）求证：求f(1)及
的值（写成关于p的表达式）；
（Ⅱ）求证 f(x)在（0，+∞）上是减函数；
（Ⅲ）（理科学生作）设
。数列
的前n项和为
，当且仅当n=5时，取得最大值。求p的取值范围。
（文科学生作）设。求数列的前n项和为。
（20）（本小题满分16分）
已知抛物线方程为
（p>0），直线x+y=t与x轴的交点在抛物线准线l的右边。
（Ⅰ）求证：直线与抛物线总有两个交点。
（Ⅱ）设直线与抛物线的交点为A，B，且OA⊥OB，求p关于t的函数的表达式p=f(x)；
（Ⅲ）（理科学生作）在的条件下，若t变化，使得原点O到直线AB的距离不大于，求p的取值范围。
（文科学生作）在（Ⅱ）的条件下，若t变化，使得原点O到直线AB的距离等于，求p的取值范围。
高三数学第二学期期末适应性练习
参考答案及评分标准
一、选择题（每小题5分，共50分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | D | B | A | C | C | C | A | D | B |
二、填空题：本大题共4小题，每小题4分，共16分。
11．50π；
12．
；
13．[-4，-π）∪[-2，0）∪[1，π）；
14．
三、解答题：本大题共6个小题，共84分。解答应写出文字说明、证明过程或演算步骤。
15．（本小题满分14分）
解：原不等式等价于
（*）…………2分
（1）当a>1时，由（*）得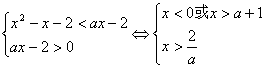
…………6分
又
，a+1>2，所以x>a+1 …………10分
（2）又当0<a<1时，由（*）得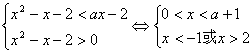
又a+1<2，所以解集为空集φ。…………14分
综上，当a>1时，解集为{xx>a+1}；当0<a<1时，解集为φ。
16．（本小题满分14分）
解：（Ⅰ）
…………4分
。…………6分
∵y的最小正周期T=π。 ∴ω=1。…………8分
∴
， ∴a=1。…………10分
（Ⅱ）由（Ⅰ）知a=1，ω=1，
∴
。
∴曲线y=f(x)的对称轴方程为
。…………12分
对称中心的坐标为
。…………14分
17．（本小题满分14分）
（Ⅰ）证明：过
作
，垂足为E，连BE。
∵侧面
底面ABC，∴
底面ABC。
∴
为侧棱
与底面所成的角。…………2分
故
，BE为在底面ABC上的射影。
又已知三棱柱的各棱长为a，故△
为等边三角形，而，
∴E为AC的中点，则在等边△ABC中，BE⊥AC，
由三垂线定理知。…………5分
（Ⅱ）证明：连交
于F，连结DF，则在菱形
中，F为中点，又D是BC之中点
∴FD∥，又FD在平面内，
∴∥截面…………9分
（Ⅲ）作
交AC的延长线于H，作HG⊥AD交AD的延长于G，连结
。
则
为二面角的平面角。…………12分
在Rt△
中，
，
在Rt△HAG中，
在Rt△
中，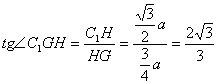
…………14分
18．（本小题满分12分）
解：（Ⅰ）设圆的周长为c，则
得
…………2分
又设出发x个单位时间后，粒子转过第三圈，则
，
即：
，
…………4分
由于x>0，∴
。
因此，转完第三圈所许需的时间为
单位时间。…………6分
（Ⅱ）设出发t 个单位时间后走完第x圈，
则
，解得
…………8分
而转完第x-1圈所用的时间
依题意：t-t′≤1，
即 
…………10分
∴49+240x≥3721， ∴x≥15.3
故从第16圈开始，粒子走一圈所用的时间不超过1个单位时间。…………12分
19．（本小题满分14分）
解：（Ⅰ）取a=b=1，则
f(1)=2f(1)-p。故f(1)=p…………2分
又
，
且f(2)=p-1。
得：
。…………4分
（Ⅱ）设
，
研究：
。…………6分
依，可得
。
再依据当x>1时，总有f(x)<p成立，可得
。…………8分
即
成立，故f(x)在（0，+∞）上是减函数。…………9分
（Ⅲ）∵
，
∴
。…………11分
∴
。
又
。
∴数列是以
为首项，公差为-1的等差数列。…………12分
∴
。
由题意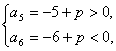
∴5<p<6。…………14分
（文科）
…………14分
20．（本小题满分16分）
解：（Ⅰ）抛物线的准线为l：
，由于直线x+y=t与x轴的交点（t，0）在准线l的右边，
所以
，即4t+p+4>0…………2分
由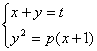
得
（*）
因为p>0，4t+p+4>0
所以
故直线与抛物线总有两个交点。…………5分
（Ⅱ）设
，
则
又由OA⊥OB得
知：
…………7分
因为A，B在直线x+y=t上，所以
故
所以 
…………9分
由p>0及4t+p+4>0，得f(t)的定义域为（-2，0）∪（0，+∞）…………11分
（Ⅲ）由原点到直线x+y=t的距离不大于，所以
即-1≤t≤1，由（Ⅱ）知t>-2且t≠0 ∴t∈[-1，0）∪（0，1] …………14分
又
令u=t+2，u∈[1，2）∪（2，3]，
易知，函数
在[1，2）上是减函数，在（2，3]上是增函数，从而，
0=g(2)<g(u) ≤g(1)=1或
所以当t∈[-1，0）时，0<p≤1，
当t∈（0，1]时，
…………16分
（文科）因为原点到直线的距离为
所以
，可得t=±1。…………14分
当t=1时，
；
当t=-1时，
。…………16分