高三第三次月考数学试卷（理科）
一、选择题:本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中,只有一
个是符合题目要求的.
1．设
（
为非零实数），若
，则
的值为
A．1 B．3 C．5 D．不确定
2．已知直线
与
平行，则实数a的取值是
A．－1或2 B．0或1 C．－1 D．2
3．不等式
的解集为
Ａ．
Ｂ．
Ｃ．
Ｄ．
4．已知
，且
，点
在线段
的延长线上，则点的坐标为
A．（
，
） B．（
，
） C．（4，－5） D．（－4，5）
5．设
, 夹角为60°, 则
等于
A．37
B．13
C．
D．
6．若
是数列
的前
项和，且
则是
A．等比数列，但不是等差数列 B．等差数列，但不是等比数列
C．等差数列，而且也是等比数列 D．既非等比数列又非等差数列
7．过原点且与圆
截得的弦长为
的一条直线的方程是
A．
B．
C．
D．
8．函数
的最大值为
A．
B．
C．
D．2
高三第三次月考数学（理）试卷第1页（共3页）
9．
、
、
、
、
、
均为非零实数，不等式
和
的解集分别为集合
和
，那么“
”是“
”的
A．充分非必要条件. B．必要非充分条件.
C．充要条件 D．既非充分又非必要条件.
10．若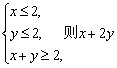
的取值范围是
A．[2，6] B．[2，5] C．[3，6] D．[3，5]
11．若
，则下列不等式：①
；②
；
③
；④
中一定成立的是
A．①②③ B．①②④ C．①② D．②④
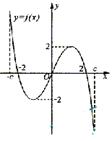
12．
是定义在区间
上的奇函数，其图象如图所示：令
，则下
|
）的叙述正确的是
A．若
,则函数
的图象关于原点对称.
B．若
,则方程
有大于2的实根.
C．若
,则方程有两个实根.
D．若
,则方程有三个实根.
二、填空题:本大题共4小题,每小题4分，共16分.把答案填在答卷纸中相应题号的横线上.
13．若
是方程
的解，其中
则
14．已知直线
，
过点
，并且它们的方向向量
满足
，那么的方程是
.
15．设集合
, 则集合
且
= ______
16．设
，利用课本中推导等差数列前项和的公式的方法，可求得
+
高三第三次月考数学（理）试卷第2页（共3页）
的值为______________________.
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
17．（本小题满分12分）已知函数
上的偶函数，其图象关于点
对称，且在区间
上是单调函数.求
的值.
18．（本小题满分12分）
已知：
、
、
是同一平面内的三个向量，其中=（1，2）
（1）若
，且//，求的坐标；
（2）若=
且
与
垂直，求与的夹角
的余弦值.
19．（本小题满分12分）已知数列
是等差数列，且
（1）求数列的通项公式；
（2）令
求数列
前项和的公式.
20．（本小题满分12分）设
，函数
(1)求
的值，使函数有最大值；
(2)若
，证明：
.
21．（本小题满分12分）经市场调查分析知，某地明年从年初开始的前个月，对某种商品需求总量
（万件）近似地满足下列关系：
（1）写出明年第个月这种商品需求量
（万件）与月份的函数关系式，并求出哪几个月的需求量超过1.4万件；
（2）若计划每月该商品的市场投放量都是
万件，并且要保证每月都满足市场需求，则至少为多少万件？
22．（本小题满分14分）已知函数
的图像上有两点
,
满足
且
,
（1）求证:
；
（2）问：能否保证
中至少有一个为正数？请证明你的结论.
高三第三次月考数学（理）试卷第3页（共3页）
第三次月考
数学（理科）参考答案
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| B | C | B | A | C | B | D | A | D | A | C | B |
2003．12
一、选择题（每小题5分，共60分）
二、填空题（每小题4分，共16分）
13．
14．
15．
16．
三、解答题（共74分）
17．解：由是偶函数，得
即
，……1分
所以
，对任意都成立，且
，……2分
所以得
.依题设
，所以解得
.……4分
由的图象关于点对称，得
，
取
，得
,……6分
8分
……9分
……10分
……11分
……12分
18．（1）解： 因为=（1，2）且//，可设
，……2分
又，所以
；……6分
（2）解：由已知得
，因为与垂直，故
…8分
.……10分
.……12分
钱高第三次月考参考答案（理）第1页(共3页)
19．（1）解：因为数列是等差数列，且可得
，从而
；……3分
（2）解：由（1）得
（
），设
的前项和为,
Ⅰ）当时，
；……4分
Ⅱ）当
时，
；……6分
Ⅲ）当
且
时，
①
②……8分
①-②得，
…10分
显然，时也满足上式，因此：当时，；当时，
.……12分
20．（1）解：当
时，
的最大值是
，这与题设矛盾.
∴
，即是二次函数……1分，∵ 
…… 3分
∴有最大值等价于
且
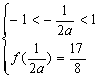……6分
即，解得：a＝－2 ……7分
(2)∵ 
，∴ 
……8分
……9分
……10分
……12分
钱高第三次月考参考答案（理）第2页(共3页)
21．（1）解：当
，时，
……………………2分
当
时，
（经检验对也成立）
∴
………………………………5分
解不等式
得
，∵
即第6个月的需求量超过1.4万件.………………………………7分
（2）解：由题设可知，对于
恒有：
，
即
……………………9分
当且仅当
时，
.
∴每月至少投放1.14万件.…………………………………………12分
22．（1）证明：因为
即
……2分
…4分
又
……6分
（2）解：设
……8分
由已知
，
,……10分
上为增函数,
……12分
同理,当
.……14分
钱高第三次月考参考答案（理）第3页(共3页)