高三第三次月考数学试卷（文科）
一、选择题:本大题共12小题，每小题5分，共60分.
1. 已知函数
的值域为集合
，函数
的值域为集合
，则
A.
B. 
C.
D.
2. 已知直线
与
平行，则实数a的取值是
A．－1或2 B．0或1 C．－1 D．2
3. 函数
在区间
上是 A．增函数 B．减函数 C．奇函数 D．偶函数
4. 以
和
为直径端点的圆的方程是
A．
B．
C．
D．
5. 不等式
的解集为
Ａ．
Ｂ．
Ｃ．
Ｄ．
6. 已知向量
，则
分
的定分比的值为：
A．
B．
C．
D．
7.过原点且与圆
截得的弦长为
的一条直线的方程是
A．
B．
C．
D．
8.台风中心从A地以每小时20千米的速度向东北方向移动，离台风中心30千米内的地
区为危险区，城市B在A的正东40千米处，B城市处于危险区内的时间为
A． 0.5小时 B． 1小时 C． 1.5小时 D． 2小时
9. 若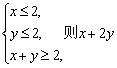
的取值范围是
高三第三次月考数学（文）试卷第1页（共3页）
A．[2，6] B．[2，5] C．[3，6] D．[3，5]
10. 由于电子技术的飞速发展，计算机的成本不断降低，若每隔5年计算机的价格降低
，现在价格8100元的计算机15年后的价格为
A．300元 B．900元 C．2400元 D．3600元
11. 若
，则下列不等式：
①
；②
；③
； ④
中一定成立的是
A．①②③ B．①②④ C．①② D．②④
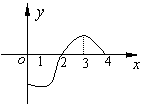
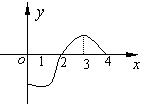12. 已知
是定义在
上的函数,的图象
如图所示,那么不等式
的解集为
A.
B.
C.
D.
二、填空题:本大题共4小题,每小题4分，共16分.把答案填在答卷纸中相应题号的横线上.
13. 函数
的最小正周期T=
.
14. 函数
满足
写出一个满足上述条件的函数____________.
15.已知直线
，
过点
，并且它们的方向向量
满足
，那么的方程是
.
16.若函数
的图象关于
对称，则
=______________.
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
17.（本小题满分12分）已知函数
上的偶函数，其图象关于点
对称，且在区间
上是单调函数.求
的值.
18.（本小题满分12分）已知等差数列前三项为
，前
项的和为
，
．
（1）求
及
的值；
高三第三次月考数学（文）试卷第2页（共3页）
（2）求
.
19．（本小题满分12分）已知点
和
，圆
：
，当圆与线段
没有公共点时，求
的取值范围.
20. （本小题满分12分）
已知：
、
、
是同一平面内的三个向量，其中=（1，2）
（1）若
，且//，求的坐标；
（2）若=
且
与
垂直，求与的夹角
的余弦值.
21. （本小题满分12分）某租赁公司拥有汽车100辆. 当每辆车的月租金为3000元时，可全部租出. 当每辆车的月租金每增加50元时，未租出的车将会增加一辆. 租出的车每辆每月需要维护费200元.
（1）当每辆车的月租金定为3600元时，能租出多少辆车？
（2）当每辆车的月租金定为多少元时，租赁公司的月收益最大？最大月收益是多少元？
22.（本小题满分14分）设二次函数
，若
且
.
（1）试证
；
（2）试比较
与
之间的大小关系；
（3）试比较
与
之间的大小关系.
高三第三次月考数学（文）试卷第3页（共3页）
第三次月考
数学（文科）参考答案
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| D | C | A | D | B | D | D | B | A | C | C | C |
2003．12
一、选择题（每小题5分，共60分）
二、填空题（每小题4分，共16分）
13．
14．
或
15．
16．6
三、解答题（共74分）
17．解：由是偶函数，得
即
，……1分
所以
，对任意
都成立，且
，……2分
所以得
.依题设
，所以解得
.……4分
由的图象关于点对称，得
，
取
，得
,……6分
8分
……9分
……10分
……11分
……12分
18．（1）解：由题意得，
，故
……2分，
所以
，……4分，因此
……6分
（2）解：由（1）得，
……8分，
钱高第三次月考参考答案（文）第1页(共3页)
所以
……10分，
.……12分.
19．解：由题意得线段所在的直线方程为：
且
……2分，
圆与线段没有公共点等价于：
①圆与线段相离，此时有：
且；……6分，
②线段在圆内，此时有：
或
；……10分
综上，
时圆与线段没有公共点。
………………………………………………………………12分
20．（1）解： 因为=（1，2）且//，可设
，……2分
又，所以
；……6分
（2）解：由已知得
，因为与垂直，故
…8分
.……10分
.……12分
21．（1）当每辆车的月租金定为3600元时，未租出的车辆数为
，
所以这时租出了88辆车. ……4分
（2）设每辆车的月租金定为x元，则租赁公司的月收益为
，……7分
整理得
.…9分
所以，当x=4100时，最大，最大值为
，……11分
即当每辆车的月租金定为4100元时，租赁公司的月收益最大，最大月收益为304200元.
………………………………………………………………12分
22．（1）
钱高第三次月考参考答案（文）第2页(共3页)
………………2分
……………………………………4分
（2）令
则
……6分
研究：
这个由于
的缘故。
所以
……………………………………9分
（3）研究
…………………………………………12分
因此 当a>0时，
当a<0时，
…………14分
钱高第三次月考参考答案（文）第3页(共3页)