高三第四次模拟数学试题
(满分:150分 考试时间:120分钟)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一项符合题目要求。
1.已知全集I,M、N是I的子集,若I=M∪N,M∩N≠Φ,则下列关系中不正确的是
( )
|
2.条件![]() ,条件
,条件![]() ,则
,则![]() 是
是![]() 的 ( )
的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
3.某学生离家去学校,一开始跑步前进,跑累了再走余下的路程。下列图中纵轴表示离校
的距离,横轴表示出发后的时间,则较符合学生走法的是 ( )
 |  |  |  |
y y y y
o x o x o x o x
A B C D
4.已知某数列前![]() 项之和
项之和![]() 为,且前
为,且前![]() 个偶数项的和为
个偶数项的和为![]() ,则前
,则前![]() 个奇数项的和
个奇数项的和
为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.在三角形ABC中“cosA+sinA=cosB+sinB”是“c=90°”的 ( )
A.充分非必要条件 B.必要非充分条件C.充要条件 D.非充分非必要条件
6.双曲线![]() 的离心率
的离心率![]() ,则k的取值范围是 ( )
,则k的取值范围是 ( )
A.(-3,0) B.(0,12) C.(-12,0) D.(-60,-12)
7.已知函数f(x)=log2(x-1),则 ( )
A.f(3x)<f(32x) B.f(3x)>f(32x)
C.f(3x)=f(32x) D.不能确定f(3x)与f(32x)大小关系
8..△ABC的三边AB=2,BC=3,AC=4,D是以△ABC的外接圆为大圆的球面上的一点,
DA=DB=DC,则球面积为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.不等式组 ![]() 表示的平面区域是 ( )
表示的平面区域是 ( )
A.矩形 B.三角形 C.直角梯形 D.等腰梯形
10.函数![]() 是 ( )
是 ( )
A.最小正周期为2π的奇函数 B.最小正周期为2π的偶函数
C.最小正周期为π的奇函数 D.最小正周期为π的偶函数
11.点P是曲线![]() 上移动,设点P处切线倾斜角为
上移动,设点P处切线倾斜角为![]() ,则
,则![]() 的取值范围是
的取值范围是
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
12.某地每年消耗木材约20万![]() ,每
,每![]() 价240元,为了减少木材消耗,决定按
价240元,为了减少木材消耗,决定按![]() 征收木
征收木
材税,这样每年的木材消耗量减少![]() 万
万![]() ,为了既减少木材消耗又保证税金收入每年
,为了既减少木材消耗又保证税金收入每年
不少于90万元,则![]() 的范围是 ( )
的范围是 ( )
A.[1,3] ![]() B.[2,4] C.[3,5] D.[4,6]
B.[2,4] C.[3,5] D.[4,6]
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上。
13.设![]() ,则
,则![]() 的
的
是 .
14.已知椭圆![]() 与双曲线
与双曲线![]() 有相同焦点,则实数t=
有相同焦点,则实数t=
15.已知![]() ,
,![]() ,则
,则![]() 的值等于 .
的值等于 .
16.给出下列四个命题: ①函数![]() 为奇函数的充要条件是
为奇函数的充要条件是![]() =0;
=0;
②若凸多面体各个面都是六边形,则2F=V-2(其中F是面数,V是顶点数);
③函数![]() 的反函数是
的反函数是![]() ;
;
④若函数![]() 是偶函数,则函数
是偶函数,则函数![]() 的图象关于直线
的图象关于直线![]() 对称。其中所
对称。其中所
有正确命题的序号是 .
答 题 卡
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题
13. 14. 15. 16.
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤。
17.(本大题满分12分)设![]() 、
、![]() 是两个不共线的非零向量(t∈R)
是两个不共线的非零向量(t∈R)
①若![]() 与
与![]() 起点相同,t为何值时,
起点相同,t为何值时,![]() ,t
,t![]() ,
,![]() (
(![]() +
+![]() )三向量的终点在一直线上?
)三向量的终点在一直线上?
②若![]() =
=![]() 且
且![]() 与
与![]() 夹角为60°,那末t为何值时
夹角为60°,那末t为何值时![]() -t
-t![]() 的值最小?
的值最小?
18.(本小题满分12分)
一名学生骑自行车上学,从他的家到学校的途中有6个交通岗,假设他在各交通岗遇到红灯的事件是独立的,并且概率都是![]()
(1)求这名学生首次遇到红灯前,已经过了两个交通岗的概率.
(2)(理)求这名学生在途中遇到红灯数ξ的期望与方差.
(文)求这名学生在途中恰好遇到3次红灯的概率.
19.(注意:在以下甲、乙两题中任选一题作答,如果两题都作答,只以甲题记分,本小题
满分12分)
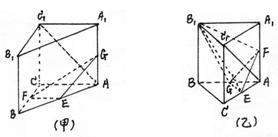
(甲)如图,在直三棱柱ABC—A1B1C1中,AC=BC=AA1,∠ACB=90°,E、F分别是AB、
BC的中点,G是AA1上的点。
(Ⅰ)如果![]() ,试确定点G的位置;
,试确定点G的位置;
(Ⅱ)在满足条件(Ⅰ)的情况下,试求![]() 的值。
的值。
(乙)如图,在直三棱柱ABC—A1B1C1中,AC=BC=AA1=2,∠ACB=90°,E、F、G分别是
|
(Ⅰ)求异面直线AC1与GF所成的角;
(Ⅱ)求三棱柱锥B1—EFG的体积.
20.(本小题满分12分)
已知:0<θ<π,等比数列{an}中,![]() ,
,
(1)问![]() 是数列{an}中的第几项?
是数列{an}中的第几项?
(2)设{an}的前n项和为Sn,若![]() 存在,求θ的取值范围.
存在,求θ的取值范围.
21.(本小题满分12分)
某沿海城市计划今年起在江河入口处对一片滩涂每年都实行围垦造地。
(1)由于围垦土地势较低,为了防涝需购置设备建排水站所需经费与当年所围土地面积x(公项)的平方成正比,比例系数为a,又设围垦前每公顷面积的年平均收入为b元,围垦后每公顷面积的年平均收入为c元,那么为使所围垦面积的年收入不少于当年建设排水站的支出与围垦前的年收入之和,试求所围垦面积x(公顷)的最大值(a、b、c为常数).
(2)为了环保最终围垦造地的总面积不允许超过现有滩涂面积的![]() ,因此计划围垦造地的面积每年以1%的速度递减,问今年围垦面积最多只能占现有滩涂面积的百分之几?
,因此计划围垦造地的面积每年以1%的速度递减,问今年围垦面积最多只能占现有滩涂面积的百分之几?
22.(本小题满分14分)
已知点F(0,![]() ),上半平面内的点P到F和x轴的距离之和为
),上半平面内的点P到F和x轴的距离之和为![]()
(1)求动点P的轨迹;
(2)设动点P的轨迹是C1,曲线C1交y轴于M。A、B是曲线C1上满足∠AMB=![]()
的两点,证明直线AB与y轴交于一定点.
数学试题参考答案
一、 选择题
1.D 2.C 3.D 4.B 5.B 6.C 7.A 8.A 9.B 10.A 11.B 12.B
二、填空题13.(理)4 (文)(![]() ) 14.1 15.③④ 16.2-x-2
) 14.1 15.③④ 16.2-x-2
三、解答题17.①设![]() -t
-t![]() =m[
=m[![]() -
-![]() (
(![]() +
+![]() )](m∈R) 化简得
)](m∈R) 化简得![]()
![]() =
=![]()
![]()
∵![]() 与
与![]() 不共线 ∴
不共线 ∴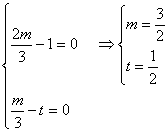
∴t=![]() 时,
时,![]() 、t
、t![]() 、
、![]() (
(![]() +
+![]() )终点在一直线上 ②
)终点在一直线上 ②![]() -t
-t![]() 2=(
2=(![]() -t
-t![]() )2=
)2=![]() 2+t2
2+t2![]() -2t,
-2t,
![]()
![]() cos 60°=(1+t2-t)
cos 60°=(1+t2-t)![]() 2, ∴t=
2, ∴t=![]() 时,
时,![]() -t
-t![]() 有最小值
有最小值![]()
18解:(1)∵这名学生第一、二个交通岗未遇到红灯,第三个交通岗遇到红灯……2分
![]() …………………………………6分
…………………………………6分
(2)(理)![]() ……………………………………………………8分
……………………………………………………8分
![]() ……………………………………………………10分
……………………………………………………10分
![]() …………………………………………12分
…………………………………………12分
(文)![]() ……………………………………………12分
19(甲)解:(Ⅰ)以C为原点,
……………………………………………12分
19(甲)解:(Ⅰ)以C为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴建立坐标系。2分
轴建立坐标系。2分
设AC=2,则C(0,0,0),A(0,2,0),C1(0,0,2),E(1,1,0)……4分
设G(0,2,![]() ),则
),则![]() ……6分
……6分
由![]() 得
得![]() ,即0×(-1)+(-2)×1+2
,即0×(-1)+(-2)×1+2![]() =0,解得
=0,解得![]() =1,
=1,
即点G为AA1的中点 ……8分
(Ⅱ)![]() ……10分
……10分
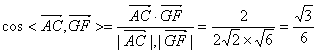 ……12分
……12分
(乙)解(Ⅰ)连结A1B、A1C,由已知得A1B//FG. ……2分
![]() 平面A1ACC1,且AC1 ⊥A1C,A1B 在平面A1ACC1上的射影为A1C.
平面A1ACC1,且AC1 ⊥A1C,A1B 在平面A1ACC1上的射影为A1C.
由三垂线定理,得AC1 ⊥A1B ……4分
![]() 即AC1与GF所成的角为90°……6分
即AC1与GF所成的角为90°……6分
(Ⅱ)![]()
![]() =
=![]() ……8分
……8分
点E到平面AA1B1B的距离为![]() ……10分
……10分
![]() ……12分
……12分
20解:(1)![]() …………2分
…………2分
又![]()
![]() ………………………………5分
………………………………5分
![]() 是{an}的第5项………………………………6分
是{an}的第5项………………………………6分
(2)![]()
又∵{an}是等比数列,∴q≠0…………………………………………8分
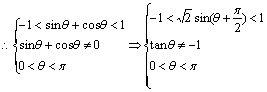 …………………………10分
…………………………10分
![]() ………………………………………………12分9.
………………………………………………12分9.
21.(1)围垦x公顷土地可得收入为cx元,故cx-(ax2+bx)≥0 即x[ax+(b-c)]≤0
当b≥c时,![]() ,不能围垦,当b<c时
,不能围垦,当b<c时 ![]() ,故围垦面积最大值为
,故围垦面积最大值为![]() (公顷)
(公顷)
(2)设该市现有滩涂面积为M公顷,今年围垦土地面积为x公顷,则x+x(1-1%)+x(1-1%)2+……≤![]()
![]() ,故今年所围垦面积最多只能是滩涂的0.25%.
,故今年所围垦面积最多只能是滩涂的0.25%.
22.设P到x轴距离为PQ ,P到直线![]() 的距离为PR.
的距离为PR.![]()
![]()
![]() ∴P的轨迹是以F(0,
∴P的轨迹是以F(0,![]() )为焦点
)为焦点
![]() 为准线的抛物线在上半平面的部分方程为
为准线的抛物线在上半平面的部分方程为![]()
(2)设A(x1,4-x) B(x2,4-x2 2 ) 又M(0,4)∴![]()
![]()
由x1≠x2得(x1+x2)x+y-3=0,它与y轴交点为(0,3)是一个定点.