高考第一轮复习单元测试（五）
不等式
一、选择题（每小题5分，共60分）
1．下列不等式中，解集为R的是（ ）．
A．
B． 
C．
D．
2．下列命题中，使命题
是命题
成立的充要条件的一组命题是（
）
A．
B．
C．
D．
3．已知0＜a＜b＜1，则下列不等式成立的是（ ）
A．
B．
C．
D．
4．已知
，
，则
的取值范围是（
）
A．全体实数 B．
C．
D．
5． 设A（1，1）和P
分别是直线
上的一个定点和一个动点，那么
的最小值是（
）
A．
B．16
C．
D．2
6．
已知
是R上的增函数，
，
其上的两点，那么
的解集的补集是（
）
A．
B．
C．
D．
7．等差数列
和等比数列
，它们的首项是相等的正数，且第2n＋1项也相等，则下列判断中正确的是（
）．
A．
B．
C．
D．
8．设实数x、y满足
，则
的最大值是（
）
A．
B．
C．
D．
9． 已知
，且
，设
，则（ ）
A．
B．
C．
D．的正负不确定
=1=
10．（文）为R上的奇函数，且在
上是减函数，
，则（ ）
A．
B． 
C． 
D． 
（理）定义在R上的偶函数在上是增函数，且
，那么
的取值范围是（ ）
A．
B．
C．
D．
11．某债券市场常年发行三种债券，A种面值为1000元，一年到期本息和为1040元；B种
贴水债券面值为1000元，但买入价为960元，一年到期本息和为1000元；C种面值为1000
元，半年到期本息和为1020元. 设这三种债券的年收益率分别为a, b, c，则a, b, c的大小关
系是（ ）
A．
B．
C．
D．
12．（文）设，
都是R上的奇函数，
=
，
=
，则不等式
的解集为（ ）
A．
B．
C．
D．
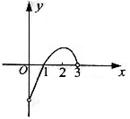(理) 已知的定义在（－3，3）上的奇函数，当0＜x＜3时，的图象如图所示，那么不等式
的解集是
（ ）
A．
B．
C．
D． 
二、填空题（每小题4分，共16分）
13．不等式
的解集是_________________________
14．若
，则
的最小值是_________________________
15．已知
，
，则
与2的大小关系是__________________
16．若实数
满足
，且
恒成立，则
的取值范围是____________________
三、解答题（共74分）
=2=
17．（本题满分12分）解不等式：
。
18．（本题满分12分）若正数
，
满足
，求
的最小值，并指出取最小值时对应的的值。
19．（本题满分12分）
（文）若
，
，
求证：①
； ②
；
（理）设
，
，
，当
，
。
求证：①
； ②当时，
。
20．（本题满分12分）某产品在一个生产周期内的总产量为100吨，平均分若干批生产，设每批生产需要投入固定费用75元，而每批生产直接消耗的费用与产品数量的平方成正比，已知每批生产10吨时，直接消耗的费用为300元（不包括固定费用）。
（1）求此产品在一个生产周期内的总费用（固定费用和直接消耗的费用）与每批生产量的函数关系式；
（2）求出平均分多少批生产时总费用最小，并求出此时的最小总费用。
21．（本小题满分12分）已知
，
，
，
；
（1）比较与的大小；
（2）设
，
,求证：
；
22．（本小题满分14分）已知函数在R上是增函数，
。
（1）求证：如果
；
（2）判断（1）中的命题的逆命题是否成立？并证明你的结论；
（3）解不等式
。
=3=
高考第一轮复习单元测试（五）
不等式参考答案
一、选择题（每小题5分，共60分）
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| D | D | B | B | C | C | A | D | B | C | D | B |
二、填空题（每小题4分，共16分）
13．
14．
15．
16．
三、解答题（共74分）
17．解：不等式可化为：
解之得：
或
，
所以不等式的解集为：
。
18．解：∵是正数，且
∴
，
当且仅当
时等号成立，所以的最小值为9。
19．文科略
理（1）证明：∵当时，，令
，则
；
（2）证明：由（1）得：
，
而 
，
由于，所以，当时，。
20．（1）解：设每批生产量为
吨，总费用为
元，由题意可算出正比例系数
，
∴ 
=4=
（2）解：∵
，
当且仅当
，即
时，
，此时应分20批。
答：平均分20批时，总费用最小，最小值为3000元。
21．（1）解：∵
，
∵
所以，
即
；
（2）证明：由（1）得
，
，…，
所以，
=
=
=
。
因此，当，时,。
22．（1）证明：∵ 在
上是增函数，且
，即
同理，
，∴
；
（2）逆命题是真命题，因为它的否命题是：若
，
下面证明它的是真的，过程（略）与（1）类似，
又 ∵逆命题与否命题真假性相同，所以逆命题成立，即若，则为真；
（3）由（2）得，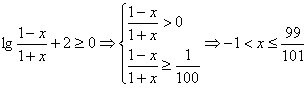
，
所以，解集为
。
=5=