高考模拟试题(一)
一、选择题(本大题共有12 个小题,每个小题5分,共60分,在每个小题给出的四个选择项中只有一项是符合题目要求).
1.在![]() 中,
中,![]()
![]() 四个条件中,是
四个条件中,是![]() 的充分且必要条件的有:( )
的充分且必要条件的有:( )
(A)1个; (B)2个; (C)3个 ; (D)4个.
2.已知![]() 是直线
是直线![]() 上定点,M是平面上的动点,则
上定点,M是平面上的动点,则![]()
![]() 的最小值是( )
的最小值是( )
(A)![]() (B)
(B) ![]()
(C)![]() (D)
(D) ![]()
3.若三数![]() 成等差数列,且
成等差数列,且![]() 又成等比数列,且
又成等比数列,且![]() 的值是( )
的值是( )
(A)0; (B)1; (C)0或1; (D)不存在.
4.设函数![]() 的图象如图所示,则
的图象如图所示,则![]() 的大小关系是( )
的大小关系是( )
(A)![]() (B)
(B) ![]()
(C) ![]() (D)
(D)![]()
5.已知直线![]() 的参数方程为
的参数方程为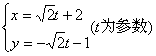 ,若以原点为极点,以
,若以原点为极点,以![]() 轴的正半轴为极点的极坐标系中,点P的极坐标为
轴的正半轴为极点的极坐标系中,点P的极坐标为![]() 则点P到直线
则点P到直线![]() 的距离为( )
的距离为( )
(A)1;
(B)![]() ; (C)1
;
(D)
; (C)1
;
(D) ![]() .
.
6.函数![]() 有反函数
有反函数![]() ,把
,把![]() 的图象在直角坐标平面内绕原点逆时针方向转动
的图象在直角坐标平面内绕原点逆时针方向转动![]() 后得到另一个函数的图象,则另一个函数是( )
后得到另一个函数的图象,则另一个函数是( )
(A) ![]() ; (B)
; (B)![]() ; (C)
; (C)![]() ; ( D )
; ( D )![]() .
.
7.一个半径为![]() 的球,在一个内半径也为
的球,在一个内半径也为![]() 的园柱形槽内恰好可以无滑动地滚动一周,设球的表面积为
的园柱形槽内恰好可以无滑动地滚动一周,设球的表面积为![]() ,槽的内壁面积为
,槽的内壁面积为![]() ,则
,则![]() 与
与![]() 的大小关系是( )
的大小关系是( )
(A)![]() (B)
(B) ![]() (C)
(C) ![]() (D) 不确定.
(D) 不确定.
8.若关于![]() 方程
方程![]() 有解,则实数
有解,则实数![]() 的取值范围是( )
的取值范围是( )
(A)![]() (B)
(B)![]() ;
;
(C)![]() ;
(D)
;
(D)![]() .
.
9.在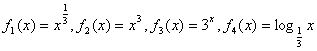 四个函数中,当
四个函数中,当![]() 时,使
时,使![]() 成立的函数是( )
成立的函数是( )
(A)![]() ; (B)
; (B)![]() ; (C)
; (C)![]() ; (D)
; (D)![]()
10.如果直角三角形的斜边与平面![]() 平行,直角边所在直线与平面
平行,直角边所在直线与平面![]() 所成角分别为
所成角分别为![]() 那么
那么![]() 满足的是条件( )
满足的是条件( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
11.在双曲线![]() 中,记左焦点为F,右顶点为A,虚轴上方的点为
中,记左焦点为F,右顶点为A,虚轴上方的点为![]() ,若
,若![]() ,则双曲线的离心率为( )
,则双曲线的离心率为( )
(A)![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]() .
.
12.某工程由下列工序组成:
| 工序 | a | b | c | d | e |
| 紧前工序 | _ | a | a | b | c. d |
| 工时数(天) | 2 | 3 | 5 | 6 | 3 |
那么工程总时数是( ) (A)12天; (B)13天; (C)14天; (D)18天.
二、填空题(本大题共4小题,每小4分,共16分,把答案填写在题中横线).
13.配制A、B两种药剂,需要甲、乙两种原料,已知配制A中药需甲原料3毫克,乙种原料5毫克,配B种药需甲原料5毫克,乙原料4毫克,今有甲原料20毫克,乙原料25毫克,若A、B两种药至少各配一剂,则配制方法有 ______ 种.
14.由一点Q到一条曲线的距离定义为QR的最短距离,这里点R在该曲线上运动,有一动点P使它到园周![]() 的距离等于它到直线
的距离等于它到直线![]() 的距离,则点P的轨迹方程是________.
的距离,则点P的轨迹方程是________.
15.已知AB、CD是夹在两平行平面![]() 之间的两条线段,
之间的两条线段,![]() ,AB=2
,AB=2
AB与平面成![]() 角,则线段CD的取值范围是________.
角,则线段CD的取值范围是________.
16.对于二项式![]() ,有下列四个命题:
,有下列四个命题:
(1)展开式中![]() ;
;
(2)展开式中非常数项的系数和是1;
(3)展开式中系数最大的项是第三者1000项和第三者1001项;
(4)当![]() 时,
时,![]() 除以2000的余数为1.
除以2000的余数为1.
其中正确命题的序号为__________.
三、解答题(共74分)
17.(本题满分12分)设![]() 且对任意
且对任意![]() 有
有![]() 解不等式
解不等式 ![]()
![]() .
.
18.(本题满分12分)设复数![]()
![]() ,其中
,其中![]() 若
若![]() 求
求![]() 的值.
的值.
19.( 本题满分12分)在四棱锥![]() 中,底面ABCD是矩形,侧棱PA
中,底面ABCD是矩形,侧棱PA![]() 底面ABCD,E、F分别是AB、PC的中点,(1)求证:
底面ABCD,E、F分别是AB、PC的中点,(1)求证:![]() ;(2)求证:
;(2)求证:![]() ;(3)当平面PCD与平面ABCD成多大角时,直线EF
;(3)当平面PCD与平面ABCD成多大角时,直线EF![]() 平面PCD?
平面PCD?
20.(本题满分12分)旅客在候车室排队等候检票,且排队的旅客按一定的速度在增加。设检票速度一定,若车站开放一个检票口,需要用半小时便可将待检旅客全部检票进站。若同时开放两个检票口,只需十分钟便可将待检旅客全部检票进站.现有一辆增开列车过境载客,必需5分钟内将旅客检票进站,问此时车站至少要同时开设几个检票口?
21. (本题满分12分)过椭圆C:![]() 上一动点P引园O:
上一动点P引园O:![]() 的两条切线PA、PB,A、B为切点,直线AB与
的两条切线PA、PB,A、B为切点,直线AB与![]() 轴、
轴、![]() 轴分别相交于M、N两点.
轴分别相交于M、N两点.
(1)已知![]() 且
且![]() ,试求直线AB的方程;
,试求直线AB的方程;
(2)求![]() 面积的最小值(O为坐标原点);
面积的最小值(O为坐标原点);
(3)椭圆C上是否存在点P,由P向园O所引的两条切线垂直?若存在,求出椭圆C的离心率![]() 的取值范围,若不存在,则说明理由.
的取值范围,若不存在,则说明理由.
22. (本题满分14分)已知函数![]() 满足
满足![]()
![]() ,
,![]() 且使
且使![]() 成立的实数
成立的实数![]() 是唯一的.
是唯一的.
(1)求函数![]() 的解析式、定义域、值域;
的解析式、定义域、值域;
(2)
如果数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,试求此数列的前3项,由此猜想数列的通项公式,并予以证明.
,试求此数列的前3项,由此猜想数列的通项公式,并予以证明.
参考答案
一 选择题:BCCBB,CBDAB,BC.
二
填空题:13. 8种; 14.![]()
![]() ; 15.
; 15. 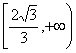 ; 16.(1)(4).
; 16.(1)(4).
三 解答题:
17.解:![]()
![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 上为减函数,
上为减函数,![]() ,
,
![]() ,
, ![]() 而
而![]() 在
在![]() 上是增函数,
上是增函数,
![]()
![]()
![]() .
.
18:解:![]()
![]()
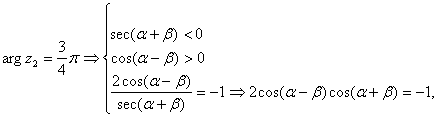
![]()
![]() (2)
(2)
代入(1)有:![]()
![]()
![]()
![]() ,
,![]() ,
, ![]() .
.
这时,![]() 或
或![]()
即![]() ,而
,而![]() 不符足
不符足![]() 舍去.故:
舍去.故: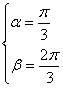
19.(1)证明:![]() 面ABCD,
面ABCD,![]()
![]() .
.
(2)取PD中点G,连FG,![]()
![]() 四边形AEFG为平行四边形。
四边形AEFG为平行四边形。
![]() 面PAD
面PAD![]() 面PAD.
面PAD.
(3)解:![]() 面ABCD,CD
面ABCD,CD![]() 是二面角P—CD—A的平面角.
是二面角P—CD—A的平面角.
当EF![]() 面PCD时,
面PCD时,![]() 面PCD,
面PCD,
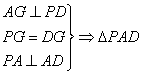 为等腰RT
为等腰RT![]() ,
,![]()
![]() .
.
当平面PCD与平面ABCD成45![]() 角时,直线EF
角时,直线EF![]() 平面PCD.
平面PCD.
20,解:设旅客增加速度为![]() 人/分,检票速度为
人/分,检票速度为![]() 人/分,原有人数为a,则
人/分,原有人数为a,则 ![]() 解得:
解得: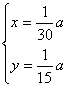 ;设应开n个捡票口,刚好五分钟将旅客检票进站,则
;设应开n个捡票口,刚好五分钟将旅客检票进站,则![]() .
.
![]() 应至少开4个检票口,可在五分钟内将旅客检票入站.
应至少开4个检票口,可在五分钟内将旅客检票入站.
21.解:(1)设![]()
则PA、PB的方程分别为:
![]()
而PA 与PB交于![]() 即
即![]()
![]()
![]() AB的直线方程为
AB的直线方程为![]() .
.
(2):由![]() 得
得![]() ,则
,则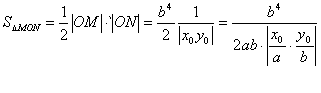
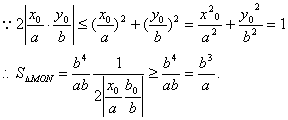
当且仅当![]() 时,
时,![]()
![]() .
.
(3)![]() 四边形OAPB为正方形,由
四边形OAPB为正方形,由
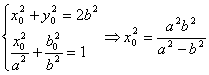
代入![]() ,得
,得![]()
所以当![]() 时,P点存在,这时
时,P点存在,这时![]() ,
,
![]() .
.
22,解:![]()
![]()
有唯一解![]() 由
由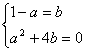 得
得![]()
![]() ,定义域为
,定义域为![]() , 值域为
, 值域为![]()
(2)![]()
![]()
![]()
![]() ,
, ![]()
相减得![]()
即:![]()
![]() .
.
猜想:![]() 用数学归类法证明之.
用数学归类法证明之.
(1)当n=1时,分式成立.
(2)假设n=k时公式成立,即:![]() ,
,
![]()
![]()
即n=k+1时分式也成立。 由(1)(2)知![]() 恒成立.
恒成立.