高考模拟数学(理)测试卷
本试卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，第I卷1至2页，第Ⅱ卷3 至8页．共150分，考试时间120分钟．
第I卷（选择题 共60分）
注意事项：
1．答第I卷前，考生务必将自己的姓名．准考证号．考试科目用铅笔涂写在答题卡上．
2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，不能答在试题卷上．
3．考试结束，监考人将本试卷和答题卡一并收回．
一．选择题（每小题5分，共60分）
1．集合M=
, P=
，则（ ）
A．MP B．PM C．P=M D．P
M=
2．“至多有一个”的否定是（ ）
A．至少有一个 B．至少有两个 C．恰有两个 D．一个也没有
3．x为三角形的一个内角，且sinx+cosx=
，则sin2x与cos2x的值依次为（ ）
A．
，
B．
， C．，
D．，
4．正四棱锥S—ABCD的侧棱长为
，底面边长为
，E是SA的中点，则直线BE与SC所成的角为
（ ）
A．90° B．60° C．45° D．30°
5．把函数y=cos(
x+
)( ＞0，
的图象向左平移
个单位，再将图上所有点的横坐标伸长到原来的2倍（纵坐标不变）所得图象的解析式为y=cosx，则（ ）
A．=，= B．=2，=
C．=，=
D．=2，=
6．
的展开式中含x4的项，则n的一个可能值是（ ）
A．1 B．3 C．6 D．10
7．一质点运动的方程为S=1-t2，则该质点在t=2时的瞬时速度为（ ）
A．2 B．-2 C．4 D．-4
8．某中学要把11台型号相同的投影仪捐送4所希望小学，每所小学至少得2台，则不同送法的种数共有（ ）
A．35种 B．21种 C．20种 D．15种
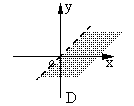
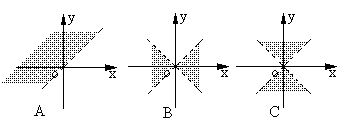
9．不等式x2-y2>0表示的区域是( )
10．双曲线
=1（a＞0，b＞0）的两焦点为F1 ．F2， F1F2=2c，P为双曲线上一点，PF1⊥PF2，则P到实轴的距离等于（ ）
A．
B．
C．
D．
11．等比数列
各项为正数，前n项的和为Sn公比
，设
+
=a，
+
=b，则a与b的大小关系是（ ）
A．a=b B．a＞b C．a＜b D．不确定
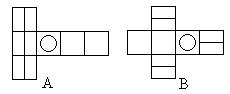
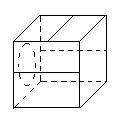
12．正方体的直观图如图所示，则其展开图是（ ）
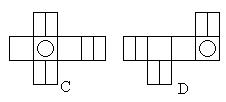
第Ⅱ卷（非选择题 共90分）
二．填空题：（本大题共4小题，每小题4分，共16分，把答案填在题中横线上．）
13．函数y=f(x)与y=log2(x-1)的图象关于直线x-1=0对称，则f(x)的定义域是_______．
14．向量a ，b的模均为2，夹角为arccos
，则a·b=________．
15．函数f(x)=x+2
的单调递增区间为
,则a=________．
16．设a＜b＜0，则
＜
，试作如下推广：设a＜b＜0，
n∈N+，则
＜_____________（要求推广后的命题为真命题）．
三．解答题：（本大题共6小题，共74分，解答应写出文字说明．证明过程或演算步骤．）
17．（本小题满分12分）
ABC中，已知角A，B，C的对边分别是a，b，c，且a2=b2+bc。求证A=2B．
18．（本小题满分12分）
已知
,
分别是x轴．y轴方向上的单位向量，
，
，
（n≥2,n∈N*），
，
（n∈N*）．
（1）
求
；
（2）求
和
的坐标．
19．（本小题满分12分）
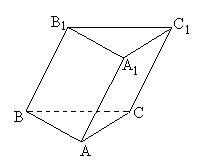
三棱柱A1B1C1-ABC的侧面BCC1B1是菱形，∠CBB1=60°，AB⊥面BCC1B1．
⑴求证B1C⊥AC1
⑵在侧面ACC1A1内是否存在一点P，使P-B1BC为正三棱维？证明你的结论．
20．（本小题满分12分）
甲乙两支足球队鏖战90分钟踢成平局，加时赛30分钟后仍成平局，现决定各派5名队员，每人射一点球，决定胜负．设甲乙两队每个队员的点球命中率均为0.5．
⑴不考虑乙队，求甲队仅有3名队员点球命中，且其中恰有2名队员连续命中的概率．
⑵求甲乙两队各射完5个点球后，再次出现平局的概率．
21．（本小题满分12分）
已知抛物线x2=2py(p＞0)在点（1，
）和（-1，）处的两切线互相垂直．
⑴求抛物线方程．
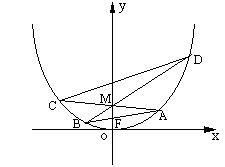⑵设四边形ABCD的四个顶点在抛物线上，焦点F在AB上，两对角线AC和BD相交于点M（0，1）．求证：OC⊥OD．
22．（本小题满分14分）
设定义在R上的函数f(x)=
图象的最高点为P (m，n)．
⑴若m＜1，n＜1，求a的取值范围．
⑵求证：对任意x,y∈R，f(x)-f(y)＜1的充要条件是m＞1．
命题人：陈 颖 严东来
高考模拟数学(理)测试卷答案
1．A 2．B 3．C 4．A 5．D 6．C 7．D 8．C 9．B 10．A
11．C 12．D
13．
14．1 15．2 16．
（或填 
等）
17．略
18．⑴ 
⑵ 
19．⑴ 略
⑵ 存在一点P，P是分
成1∶2的分点．
20．⑴ 
⑵ 
21．⑴ x2 = 2y ⑵ 证略
22．⑴ 
⑵ 提示： 