函数的极限及函数的连续性复习指导

函数的极限及函数的连续性复习指导

一、重点难点分析：
　　①
　　　
　　此定理非常重要，利用它证明函数是否存在极限。
　　② 要掌握常见的几种函数式变形求极限。
　　③ 函数f(x)在x=x₀处连续的充要条件是在x=x₀处左右连续。
　　④ 计算函数极限的方法，若在x=x₀处连续，则。
　　⑤ 若函数在[a,b]上连续，则它在[a,b]上有最大值，最小值。
　　二、典型例题
　　例1．求下列极限
　　① 　　②
　　③ 　　　④
　　解析：① 。　　
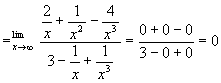　　②。
　　③。　　
　　④。
　　例2．已知，求m,n。
　　解：由可知x²+mx+2含有x+2这个因式，
　　∴ x=-2是方程x²+mx+2=0的根， 　　∴ m=3代入求得n=-1。
　　例3．讨论函数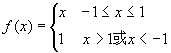的连续性。
　　解析：函数的定义域为(-∞,+∞)，由初等函数的连续性知，在非分界点处函数是连续的，
　　又，
　　∴ ， ∴ f(x)在x=1处连续。
　　由，
　　从而f(x)在点x=-1处不连续。 ∴ f(x)在(-∞,-1),(-1,+∞)上连续，x=-1为函数的不连续点。
　　例4．已知函数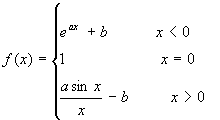, (a,b为常数)。
　　试讨论a,b为何值时，f(x)在x=0处连续。
　　解析：∵ 且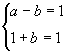， ∴ ，∴ a=1, b=0。
　　例5．求下列函数极限 　　① 　　②
　　解析：① 。
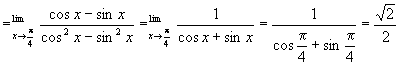　　② 。
　　例6．设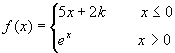，问常数k为何值时，有存在？
　　解析：∵ ，。
　　要使存在，只需， ∴ 2k=1，故时，存在。
　　例7．求函数在x=-1处左右极限，并说明在x=-1处是否有极限？
　　解析：由，，
　　∵ ，∴ f(x)在x=-1处极限不存在。
　　训练题：
　　1．已知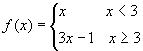，则
　　2．的值是_______。
　　3. 已知，则=______。
　　4．已知，2a+b=0，求a与b的值。
　　5．已知，求a的值。
　　参考答案：1. 3　　2. 　　3. 　　4. a=2, b=-4　　5. a=0