课时5 函数的连续性
一、复习目标
了解函数连续的意义，理解闭区间上连续函数有最大值最小值的性质.
二、例题讲解
例1．已知函数
且有如下结论：①
在点
处连续；②在点
处连续；③在点处极限不存在；④在点处极限不存在.其中正确的有___①④___.
例2．指出下列函数的不连续点：
（1）
；（2）
；
.
解：（1）由
，得
，所以函数的不连续点为.
（2）当
时，
，分母为0，当
，
不存在，所以函数的不连续点为
和.
例3．设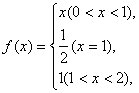
（1）求在点处的左、右极限.函数在处是否有极限？
（2）函数在点处是否连续？
（3）确定函数的连续区间.
解：（1）
∵
，
∴函数函数在处极限存在，且
.
（2）∵，且
，∴
.
∴函数在点处不不连续.
（3）函数的连续区间是(0,1),(1,2).
例4．设函数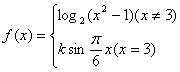
，在
处连续，试确定
的值.
解：∵
，又
，而在处连续，∴
，即
三、同步练习：《高考三人行—学生用书》P344
课时6 数学归纳法
一、复习目标
掌握数学归纳法证题的两个步骤，能运用数学归纳法证题，有初步的猜想归纳能力.
二、例题讲解
例1．设
，那么
等于（ D ）
A．
B．
C．+ D．-
例2．某个命题与正整数有关，若
时，该命题成立，那么可推得当
时该命题也成立，现已知当
时该命题不成立，那么可推得（ ）
A．当
时该命题不成立
B．当时该命题成立
C．当
时该命题不成立
D．当时该命题成立
解：如果时命题成立，那么由题设，时命题也成立.上面的判断作为一个命题，那么它的逆否命题是：如果时命题不成立，那么时命题也不成立.原命题成立，它的逆否命题一定成立，故选C.
例3．
，求证：
.
证明：略
例4．证明不等式：
证明：略
例5．已知
，是否存在自然数
，使得对任意，都能使整除
，如果存在，求出最大的值，并证明你的结论；若不存在，说明理由.
解：
，猜想能整除的最大整数是36.
下面证明能被36整除，
（1）当
时，
能被36整除；
（2）假设当
时，
能被36整除，则当时，
由归纳假设
能被36整除，而
时偶数，
∴
能被36整除，∴
能被36整除.
由（1）、（2）得能被36整除，由于，所以能整除的最大整数是36.
三、同步练习：
已知点的序列
，
，其中
，
是线段
的中点，
是线段
的，…，
是线段
的中点，….
（1）写出
与
、
之间的关系式（
）；
（2）设
，计算
，由此推测数列
的通项公式，并加以证明；
（3）求.
解：（1）当时，
.
（2）
，由此猜测
.
证法一：因为
，且
（
），所以.
证法二：数学归纳法
（3）当时，有
，
由（2）知是公比为
的等比数列，所以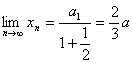
.