|
|
学科：数学 |
| 教学内容：第一章 函数与方程 |
一、考纲要求
1.理解集合、子集、交集、并集、补集等概念。了解空集和全集的意义，了解属于、包含 、相等关系的意义，能掌握有关术语和符号，能正确地表示一些较简单的集合。
2.理解逻辑联词“或”、“和”、“且”、“非”的含义，理解四种命题及其相互关系。
3.理解｜ax+b｜＜c，｜ax+b｜＞c(c＞0)型不等式的概念，并掌握它们的解法；了解二次函数、一元二次不等式及一元二次方程三者之间的关系，掌握一元二次不等式的解法。
4.了解映射的概念，在此基础上理解函数及有关的概念，掌握互为反函数的图像、定义域及值域间的关系，会求一些简单函数的反函数。
5.理解函数的单调性和奇偶性的概念，并能判断一些简单函数的单调性和奇偶性，能利用函数的奇偶性与图像的对称性关系描绘函数的图像，了解奇偶函数定义域必关于原点对称的特点。
6.理解分数指数幂、根式的概念，掌握有理指数幂的运算法则。
7.理解对数的概念，掌握对数的性质和运算法则。
8.掌握幂函数的概念及其图像和性质，在考察函数性质和运用性质解决问题时，所涉及的 幂函数f(x)=xa中的a限于在集合｛-2、-1、-
、
、1、2、3｝中取值。
9.掌握幂函数、指数函数、对数函数的概念及其图像和性质，并会解简单指数方程和对数方程。
10.会解简单的对数不等式、指数不等式及简单的函数不等式，要注意单调性和定义域的应用。
二、知识结构(见下图)
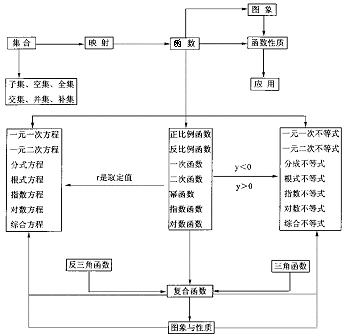
三、知识点、能力点提示
1.集合
(1)集合元素有“四性”：确定性、互异性、无序性和任意性。即集合中元素应完全确定， 不能模棱两可，集合中元素互不相同，不能重复出现；集合中元素无序关系，例如｛1、2、 3｝与｛2、1、3｝表示同一集合；集合中元素可以是具体确定的事物，而不仅限于“数、点 、式、形”。
(2)集合表示方法有三种：列举法、描述法和图示法。
(3)元素与集合，集合与集合的关系：“∈”“
”用于表示元素与集合间关系，“
”“＝”“
”“
”用于表示集合与集合间关系。
(4)集合运算有三种：交、并、补。
交集：由所有属于集合A且属于集合B的元素所组成的集合，叫做A、B的交集，记作A∩B。即
A∩B＝｛x｜x∈A且x∈B｝
并集：由所有属于集合A或属于集合B的元素所组成的集合，叫做集合A、B的并集，记作A∪B 。即
A∪B＝｛x｜x∈A或x∈B｝
补集：已知全集I、集合AI，由I中所有不属于A的元素组成的集合，叫做集合A在集合I中的补集，记作
。即
＝｛x｜x∈I，且xA｝
(5)例题赏析
例1 已知集合A＝｛x、xy、lg(xy)｝，B＝｛0、｜x｜，y｝且A＝B，求x、 y的值。
解：由A＝B可知，必有lg(xy)＝0，即xy＝1，若xy＝y，则x＝1，于是x＝xy，与集合A中元 素互异性矛盾，故xy＝｜x｜，即x＝y＝-1 符合题意，此时，A＝B＝｛1，-1，0｝，∴x＝ y＝-1
说明：通过对“集合元素有‘四性’”的应用，强化学生对概念的理解，培养学生思维的全 面性、深刻性，使之具备应用集合元素性质解决问题的能力。
例2
设I＝｛x｜x是不大于20的质数｝，且A∩
＝｛3，5｝，∩
＝｛7，19｝，∩＝｛2，17｝，则A＝ ，B＝ 。
解：由题设知，I＝｛2，3，5，7，11，13，17，19｝，因为∩＝｛2，17 ｝，A∪B＝｛3，5，7，11，13，19｝，这些元素可分三种情况，属于集A而不属于集B(由题 设为3，5)；属于集B而不属于集A(由题设为7，19)，余下的11，13既属于集A，又属于集B，
故A＝｛3，5，11，13｝，B＝｛7，11，13，19｝
注：本题可用韦恩图表示I、A、B之间的关系，其结果将更加明朗。
说明：通过对集合表示方法的训练，培养学生思维的灵活性，使之具备“数形结合”解决此类问题的能力(韦恩图法)。
例3
设A＝｛x｜x＝a2+1，a∈N｝，B＝｛y｜y＝b2-6b+10，b∈N｝， 求证：AB
证：∵A＝｛x｜x＝a2+1，a∈N｝，B＝｛y｜y＝b2-6b+10，b∈N｝＝｛y｜y＝(b-3)2 +1，b∈N｝
又∵a,b∈N，∴b-3∈｛-2，-1，0｝∪N
对于任意一元素x∈A，则x∈B
∴AB
当b-3＝0时y＝(b-3)2+1＝1∈B，而1A
∴A
B
说明：通过对集合与元素，集合与集合关系的训练，培养学生运算能力，使之具备根据条件寻求合理、简捷运算途径的能力。
例4 设A＝｛x｜(x+2)(x+1)(x-1)＞0｝，B＝｛x｜x2+px+q≤0｝，若A∪ B＝｛x｜x＞-2｝，A∩B＝｛x｜1＜x≤3｝，求p、q的值。
解：将A化简，得A＝｛x｜-2＜x＜-1，或x＞1｝，由A∪B＝｛x｜x＞-2｝，A∩B＝｛x｜1＜ x≤1｝，结合数轴，知B＝｛x｜-1≤x≤3｝，由-1和3是方程x2+px+q＝0的两根，得p＝-2 q＝-3
说明：通过对数集的交、并、补运算的训练，使学生掌握化简集合，利用数轴表示集合并进行运算的方法。
2.映射与函数
(1)映射是一种特殊的对应，即“一对一”或“多对一”但不能是“一对多”。
(2)从集合A到集合B的映射f：A→B中，A中任一元素都必须有象，但B中元素未必有原象。
(3)函数是一种特殊的映射，要求f:A→B中，A、B都是非空数集，其中A为定义域，f(A)是值域。
(4)函数的表示方法有三种：图像法、表格法和解析法。
(5)函数的三要素：定义域、值域、对应法则。
(6)函数的三特征：非空、数集、满射。
(7)例题赏析：
例5 已知(x,y)在映射f下的象是(x2+y2,x2-y2)，求点(10，8)在 f下的原象。
解：由已知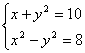得
，解得
所以所求的原象是(3，1)；(3，-1)；(-3，1)；(-3，-1)。
说明：通过本题加深对“映射”概念的理解，训练学生分析象与原象关系的能力，使之具备把映射与其它知识综合运用的能力。
例6
设f(x)是定义在R+上的函数，且满足f(xy)＝f(x)+f(y) f()＝1，求f(1)和f(4)的值。
解：∵对任意x，y∈R+均有f(xy)＝f(x)+f(y)成立
令x＝1,y＝1，得f(1·1)＝f(1)+f(1)
∴f(1)＝0
又令x＝2，y＝ 得f(2·)＝f(2)+f()
∴0＝f(2)+1 ∴f(2)＝-1
∴f(4)＝f(2·2)＝f(2)+f(2)＝2f(2)＝-2
说明：通过“函数是一种特殊的映射”，训练学生思维的敏捷性和灵活性，使之具备抽象思维能力。
例7 已知一台冷轧机共有4对减薄率为20%的轧辊，所有轧棍周长均为1600m m，若第K对轧辊 有缺陷，每滚动一周在带钢上压出一个疵点，在冷轧机输出的带钢上，疵点的间距为LK， 为了便于检修，请计算L1、L2、L3并填入下表(轧钢过程中，带钢宽度不变，且不考虑损耗)。
| 轧辊序号K | 1 | 2 | 3 | 4 |
| 疵点间距LK(mm) | 1600 |
解：第3对轧辊出口疵点间距为轧辊周长，在此处出口的两疵点间带钢体积与冷轧机出口处 两疵点间带钢体积相等，因宽度不变，故 1600＝L3·(1-0.2)
所以 L3＝1600/0.8＝2000(mm)
同理 L2＝L3/0.8＝2500(mm)
L1＝L2/0.8＝3125(mm)
填表如下：
| 轧辊序号K | 1 | 2 | 3 | 4 |
| 疵点间距LK(mm) | 3125 | 2500 | 2000 | 1600 |
说明：通过函数表示方法，训练学生分析问题能力，使之具备用表格法表示函数的能力。
例8 已知函数f(x)＝x2，g(x)为一次函数，且一次项系数大于零，若f(g (x))＝4x2-20x+25，求g(x)的表达式。
解：由g(x)为一次函数，设g(x)＝ax+b(a＞0)
∵f(g(x))＝4x2-20x+25
∴(ax+b)2＝4x2-20x+35，即
a2x2+2abx+b2＝4x2-20x+25
解得a＝2,b＝-5
故g(x)＝2x-5(x∈R)
说明：通过本题，训练学生利用待定系数法、恒等式性质解题的能力，加深对函数三要素、 三特征的理解，使之具备求复合函数解析式、定义域的能力。
3.函数性质
(1)定义域：x的取值集合。
(2)值域：y的取值集合。
(3)增减性：对于给定区间上的函数f(x)、对任意的x1，x2·x1＜x2
f(x1)＜f( x2),f(x)在区间上是增函数；x1＜x2f(x1)＞f(x2)，f(x)在区间上是减函数。
(4)奇偶性：对于函数定义域内任意x，有f(-x)＝f(x) f(x)是偶函数；f(-x)＝-f(x) f(x )是奇函数。
(5)周期性：若存在常数T(T≠0)，使对定义域内任意x都有f(x+T)＝f(x),则f(x)叫周期函数 ，T叫f(x)的一个周期，合条件的最小正数T叫f(x)的最小正周期。
(6)奇偶性与单调性
奇函数在对称区间(-b,-a)与(a，b)上增减性相同。
偶函数在对称区间(-b,-a)与(a，b)上增减性相反。
(7)奇函数、偶函数定义域必关于原点对称。对于奇函数f(x)，若f(0)有意义，则f(0)＝0；f(x)＝0。既是奇函数又是偶函数。否则会期引起歧义。
(8)例题赏析：
例9
求函数y＝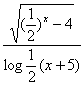
的定义域。
解：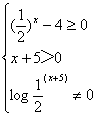
-5＜x＜-2，且x≠-4
所以定义域为(-5，-4)∪(-4，-2)
说明：给定了函数的解析式，如果未指出函数的定义域，一般而言，函数的定义域就是使解析式有意义的自变量的取值范围。
应考虑到：
(1)分式 分母≠0；
(2)偶次根式 被开方数≥0；
(3)对数 真数＞0，底数＞0，底数≠1；
(4)零指函数 底数≠0；
(5)正切
y=tgx, x≠kπ+
(k∈z)；
余切 y=ctgx, x≠kπ(k∈z)；
(6)反正、余弦｜x｜≤1。
如果是实际问题或几何问题，要根据实际情况确定函数定义域；如圆面积公式S＝πR2的定义域是R＞0。
例10 求下列各函数的值域：
(1)y＝
； (2)y＝
； (3)y＝
；
(4)若f(x)的值域是〔
，
〕，求函数g(x)＝f(x)+
的值域。
解：(1)y＝-1+
∵≠0 ∴y≠-1
故函数y＝的值域为(-∞，-1)∪(-1，+∞)
(2)由函数关系式，得 ex＝
，∵ex＞0，即＞0
解得y＞2或y＜-1，故函数的值域为(-∞，-1)∪(2，+∞)
(3)由函数关系式变形、整理，得2yx2-4yx+3y-5＝0，当y＝0时，-5＝0矛盾，故y≠0
∵x∈R
∴Δ＝(-4y)2-4·2y(3y-5)≥0，即0≤y≤5，故0＜y≤5，函数的值域为(0，5]
(4)设t＝ ∵≤f(x)≤ ∴
≤1-2f(x)≤
即t∈［，］，且f(x)＝(1-t2)，于是
g(x)＝-t2+t+＝-(t-1)2+1，t∈［，］
当t＝时，gmin(x)＝
当t＝时，gmax(x)＝
∴≤g(x)≤，故函数g(x)的值域为［，］
说明：求值域常用方法有：
(1)用配方法求二次函数的值域；(2)根据反函数求二次函数的值域；(3)对于可化为二次函数型时，利用判别式法求值域，但要注意某些限制条件；(4)利用函数的单调性求函数的值域；(5)通过函数的图像和变量代换求出函数的值域。
本题通过求函数值域，训练学生的逻辑思维及运算能力，加深对反函数、二次函数及函数单调性等数学概念的理解，使之具备思维的多向性、深刻性和批判性等能力。
例11 已知f(x)＝x3,证明f(x)在R上是增函数。
证明：设x1，x2∈R且x1＜x2，则
f(x1)-f(x2)＝x13-x23＝(x1-x2)(x12+x22+x1x2)
＝(x1-x2)［(x1+x2)2+
x22］
∵x1＜x2
∴(x1+x2)2+x22＞0,(否则x1＝x2＝0)
又x1-x2＜0
∴(x1-x2)［(x1+x2)2+x22］＜0
即 f(x1)-f(x2)＜0，f(x1)＜f(x2)
∴f(x)＝x3在R上是增函数。
说明：通过单调性证明，训练学生运算能力，使之具备将f(x1)-f(x2)化为几个能确定符号的因式的积的能力。
注意：①单调性是与“区间”紧密相关的概念，一个函数在不同的区间上可以有不同的单调性；②单调性是函数在某一区间的“整体”性质，因此定义中的x1、x2具有任意性，不能用特殊值代替。若求单调区间则应求“极大”区间。③由于定义是充要性命题，因此单调性使得自变量间的不等关系和函数值之间的不等关系可以“正逆互推”。
例12 判断下列函数的奇偶性：
(1)f(x)=2x-()X;
(2)f(x)= 
+
;
(3)f(x)=
·
;
(4)f(x)=lg(x+
);
(5)f(x)=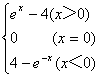
解：(1)奇函数
(2)函数定义域为(-∞，0)∪(0+∞)
f(-x)=
=(-x)
=(-x)(
)
=(-x)( 
=f(x)
所以函数为偶函数
(3)由
得x＝1
故函数的定义域为｛1｝，它不是关于原点对称的实数集，故此函数既不是奇函数，又不是偶函数。
(4)函数的定义域为R。
f(x)+f(x)=lg(-x+)+lg(x+)
=lg(-x+)(x+)=lg1=0
即 f(-x)=-f(x)
所以函数为奇数函数
(5)函数的定义域为R。
f(-x)=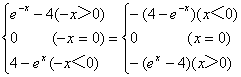
故f(x)是奇函数
注 研究函数奇偶性应注意：
(1)f(-x)=f(x)与f(-x)=-f(x)中x应是定义域内任意值；
(2)已知函数f(x)的定义域应是关于原点对称取值的实数集，否则函数是非奇非偶函数；
(3)奇函数图像关于原点对称，偶函数图像关于y轴对称。
例13 已知函数f(x)的最小正周期是8，且等式f(4+x)＝f(4-x)，对一切实数 x成立，判断f(x)的奇偶性。
解：f(-x)＝f［4-(4+x)］＝f［4+(4+x)］＝f(8+x)＝f(x)
故f(x)是偶函数。
说明：通过函数的周期性，对称性推导其奇偶性，训练学生的逻辑思维能力。使之具备正确 的思维取向，提高能力层次。
例14 已知函数f(x)是奇函数，而且在(0，+∞)上是减函数，f(x)在(-∞，0)上是增函数还是减函数?
解：设x1、x2＜0且x1＜x2，则0＜(-x2)＜(-x1)
∵f(x)在(0，+∞)上是减函数
∴f(-x2)＞f(-x1)…… (1)
又∵f(x)是奇函数
∴f(-x2)＝-f(x2)，f(-x1)＝-f(x1)代入(1)式得
-f(x2)＞-f(x1) 从而
f(x2)＜f(x1)
由此可知：函数f(x)在(-∞，0)上是减函数。
说明：通过应用奇偶性、单调性，训练学生分析问题能力使之具备转化条件解决问题的能力 。
4.二次函数在闭区间上最值问题
闭区间［α，β］上的函数f(x)＝ax2+bx+c(a≠0)，当-
∈［α，β］ 时 ，最值从f(-),f(α),f(β)中比较得出。当-［α，β］时，最值从f(α),f(β)中比较得出。
例15 求函数y＝3x2-12x+5当自变量x在下列范围内取值时的最值。
(1)0≤x≤3 (2)-1≤x≤1
解：对称轴x＝2
(1)∵2∈［0，3］ ∴当x＝2时，ymin＝-7
x＝0时，ymax＝5
(2)∵2［-1，1］ ∴当x＝1时，ymin＝-4
当x＝-1时，ymax= 20
5.反函数
(1)式子y＝f(x)表示y是自变量x的函数，设它的定义域为A，值域为C，我们从式子y＝f(x) 中解出x，得到式子x＝φ(y)，如果对于y在C中的任何一个值通过式子x＝φ(y)，x在A中 都 有唯一确定的值和它对应，那么式子x＝φ(y)就表示x是自变量y的函数。这样的函数x＝φ( y)，叫做函数y＝f(x)的反函数，记作x＝f-1(y)，即 x＝φ(y)＝f-1(y)
习惯上，一般用x表示自变量，y表示函数，为此对调式子x＝f-1(y)中的字母x、y， 把它改写成y＝f-1(x)
(2)原函数与反函数的图像关于y＝x对称。
(3)原函数与反函数在对应的区间上的增减性相同。
(4)若函数的反函数是奇函数，则原函数也是奇函数。
(5)单调函数必有反函数。
(6)f-1(f(x))＝x,x∈A，f［f-1(x)］＝x,x∈C。
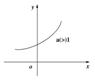
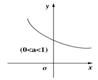
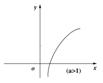
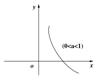
6.幂函数：y＝xa，定义域是使xa有意义的实数，图像过(1，1)点，a＞0时，在第一象限内是增函数；a＜0时，在第一象限内是减函数。
例16
已知幂函数f(x)＝x
(m∈Z)为偶函数，且在(0，+∞) 上是增函数，求f(x)的解析式。
解：∵f(x)＝x
在(0，+∞)上是增函数
∴4-(m-1)2＞0 解之得：-1＜m＜3
又∵m∈Z ∴m＝0，1，2，代入得：
f(x)＝x3,f(x)＝x4,f(x)＝x3
又∵f(x)为偶函数
∴f(x)＝x4
说明：通过求幂函数的解析式，训练学生自觉运用幂函数的性质使之具备解决待定系数法确 定幂函数解析式的能力。
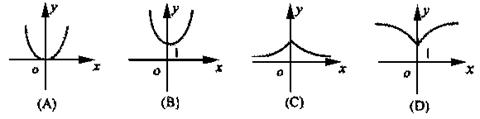
例17 函数y=a｜y｜(a＞1)的图像是( )
解：由于y=a｜x｜(a＞1)是偶函数，其图像关于y轴对称，故可先画y=ax(x≥0，a ＞1)的图像，然后再沿y轴翻折。
应选B。
说明：通过函数定义域及其奇偶性，判断值域，使学生具备从特殊到一般的辨证思维能力。
7.指数函数与对数函数
(1)对数：在指数式ab＝N中(a＞0且a≠1)，则称b叫做以a为底N的对数，记作b＝logaN, 以10为底的对数称为常用对数，记作lgN，以e为底的对数称为自然对数，记作lnN。
(2)指数运算法则(略)，对数运算法则(略)。
(3)若lgx＝a+b，其中a∈Z，b∈［0,1),则称a为x的常用对数的首数，b为x的常用对数的尾数，当x＝a×10n，1≤a＜10时，则lgx的首数为n。
(4)对数恒等式 a
＝N(a＞0，且a≠1)
对数换底公式 logaN＝logbN/logba(a、b＞0且≠1)
(5)对数函数与指数函数性质
| 指数函数 | 对数函数 | ||||||||||||
| 解析式 | y＝ax(a＞0，a≠0) | y＝logax(a＞0，a≠1) | |||||||||||
| 定义域 | x∈R | x∈R+ | |||||||||||
| 值 域 | y∈R+ | y∈R | |||||||||||
| 图 像 |
|
|
|
| |||||||||
| 性 质 | 单调性 | a＞1，R递增 | 0＜a＜1时，R递减 | a＞1时，R+递增 | 0＜a＜1时，R+ 递减 | ||||||||
| 特征点 | (0，1) | (1，0) | |||||||||||
| 值 的分 布 | x＜0 | x＝0 | x＞0 | 0＜x＜1 | x＝1 | x＞1 | |||||||
| a＞1 | 0＜y＜1 | y＝1 | y＞1 | a＞1 | y＜0 | y＝0 | y＞0 | ||||||
| 0＜a＜1 | y＞1 | y＝1 | 0＜y＜1 | 0＜a＜1 | y＞0 | y＝0 | y＜0 | ||||||
(6)例题赏析
例18
求函数y＝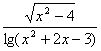
的定义域
解：要使函数有意义，必须且只需
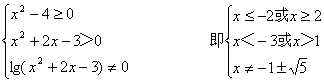
∴x＜-3或x≥2，且x≠-1-
故函数定义域为｛x｜x＜-3或x≥2，且x≠-1-｝
例19设a＞0，a≠1，又b＝(a
-a
)求loga2(b+
)n
解：∵b＝(a-a) ∴＝(a+a)
∴log
(b+)n＝loga2(a)n ＝loga2a＝
说明：通过本题，训练学生运算能力，使之具备正确应用对数、指数性质的能力。
例20
已知函数f(x)＝
(1)判断它的奇偶性。
(2)求证它是单调递增函数。
(3)求它的反函数。
解：(1)：∵10x+10-x≠0 ∴定义域为R
f(-x)＝ ＝-f(x)
∴f(x)为奇函数。
(2)：任取x1、x2∈R，且x1＜x2，则
f(x2)-f(x1)＝
＝
当x2＞x1时，10
＞1 10
＜1
∴10-10＞0
又(10
+10
)·(10
+10
)＞0
∴f(x2)＞f(x1)
∴f(x)为增函数。(变形f(x)＝
更容易些)
(3)y＝去分母得 y·102x+y＝102x-1
(1-y)102x＝1+y
当y＝1时，x无解
当y≠1时，102x＝
显然当
＞0时，即-1＜y＜1时，x有解。
当 ≤0时，x无解
∴当-1＜y＜1时，2x＝lg
即x＝lg［］ (-1＜y＜1)
∴反函数为：y＝lg (-1＜x＜1)
说明：此题f(x)的形式变化可使解题难易程度变化。本题以f(x)为载体全面地训练学生对函 数的性质的理解和运用，使之具备较强的运算能力。
例21
已知函数f(x)＝lg(x+
)-lg
证明：(1)f(x)的图像关于原点对称。
(2)f(x)为单调函数。
证明：(1)∵x∈R
f(-x)＝lg(-x+)-lg
＝lg
＝-［lg(x+)-lg
＝-f(x)
∴f(x)是奇函数，故f(x)图像关于原点对称。
(2)设x1，x2∈R，且x1＜x2
∵
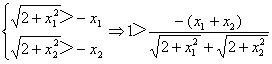
∴x2-x1＞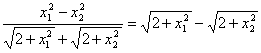
∴x2+
＞x1+
∴f(x2)＞f(x1)
∴f(x)为单调递增函数。
说明：本题通过奇偶性、单调性证明，训练学生的运算能力，使之加深对函数性质理解，具备举一反三的能力。
8.指数方程与对数方程
(1)指数方程是一种超越方程，指数方程的解法大致分类有四种：(A)af(x)＝ag(x)，其中a＞0且a≠1，利用指数函数的单调性化为代数方程：f(x)＝g(x) (B)形如a2x+b·ax+c＝0的指数方程，用换元法化为一元二次方程来解。 (C)用对数知识。如af(x)＝bg(x)(a＞0且a≠1，b＞0且b≠1)两边取对数，从而求解x (D)用图像 法求近似解。
(2)对数方程也是超越方程，对数方程的主要类型有：(A)基本型：logax＝b (B)同底数型：logaf(x)＝logbg(x) (C)：形如：log
+blogax+c＝0的代换型，各类型方程解法相对固定，均能化为代数方程解之，但要注意验根。上述类型以外的对数方程可用图像法求近似解。
(3)解对数方程时，需注意以下几点：
(A)利用公式logaM+logaN=logaMN作恒等变形可能产生增根。例如，解方程lg(2x-1)+ lg(3x-7)=0时。
(B)利用公式logaMk=klogaM作恒等变形可能失根，例如：解方程lg(x-1)2+lg(x-1)4+lg(x-1)6=12时。
(1)两边消去对数符号可能产生增根，例如解方程logaf(x)=logag(x)时
(4)例题赏析
例22 解下列方程
(1)37x-1·125x＝210x (2)7·3x+1-5x+2＝3x+4- 5x+3
解：(1)37x-1·35x·210x＝210x，得312x-1＝1
∴12x-1＝0，x＝是原方程的解
(2)7·3x+1-5x+2＝27·3x+1-5·5x+2
20·3x+1＝4·5x+23x+1＝5x+1
(
)x+1＝1 ∴x+1＝0，即x＝-1是原方程的根。
例23 解下列方程
(1)2·72x-3-3·7x-2-5＝0 (2)x3lgx＝100x5
解：(1)令7x＝t，则2t2-21t-5×73＝0
t1＝35,t2＝-
(舍)
由7x＝35得x＝1+log75是原方程的解
(2)两边取以10为底的对数，方程化为3lg2x-5lgx-2＝0，从而lgx＝2，-.解得 x＝100或x＝10
，检验知x＝100，x＝10是原方程的解。
说明：通过例1、例2，训练学生解指、对数方程的基本能力和基础方法，使之具备解较简单 指对数方程的能力。
例24
解方程：log0.5xx2-14log16xx3+40log4x
＝0
解：x＞0，当x≠1时，利用换底公式将原方程化为：
∴
∴x＝4或x＝
经检验4，都是原方程的根。
由于换底时，可能失根1，经检验x＝1是原方程的根。
∴x＝4，x＝1，x＝都是原方程的根。
说明：通过本题，训练学生寻找失根的能力，使之具备解复杂方程的能力。
9.指数不等式与对数不等式
指数不等式与对数不等式都是超越不等式，其解法与它们的方程解法有点类似(比如换元法) 。解这样的不等式需要用到指数函数与对数函数的性质，特别是单调性。对其底数是否大于 1或小于1及定义域要特别重视。
例25 解下列不等式
(1)9
-7
-12＞0
(2)log0.3
＜log0.3
(3)loga(
)
+loga(
(4)log4(3x-1)log
≤
解：(1) 9-7-12＞03
-7
-12＞0
x2-x-12＞0x＞4或x＜-3(舍)
∴原不等式的解为｛x｜x＞4｝
(2)原不等式化为：
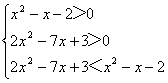解之得：3＜x＜5
∴原不等式的解集为｛x｜3＜x＜5｝
(3)原不等式化为 x2loga()+4xloga() ＞5loga()
当a＞1时，loga()＜0，则x2+4x-5＞0解得x＜-5或x＞1
当0＜a＜1时，loga()＜0，则x2+4x-5＜0解得-5＜x＜1
∴当a＞1时，原不等式解集为｛x｜x＜-5或x＞1｝
当0＜a＜1时，原不等式解集为｛x｜-5＜x＜1｝
(4)利用对数的性质将原不等式化为
［log4(3x-1)］2-2log4(3x-1)+ ＝0
令t＝log4(3x-1)得 4t2-8t+3≥0
解得：t≤或t≥
当t≤时，0＜3x-1≤2，即1＜3x≤3 ∴0＜x≤1
当t≥时，3x-1≥4
，即3x≥8+1
∴x≥2
∴原不等式的解集为｛x｜0＜x≤1或x≥2｝
说明： 通过解指数不等式与对数不等式，训练学习应用函数性质能力，使之具备解指数不 等式与对数不等式的能力。
10.综合问题
(1)函数y＝f［
(x)］可看成是函数y＝f(u)与u＝(x)复合而来的。或称y＝f［(x)］是 y＝f(u)与u＝(x)的复合函数。在此时u＝(x)的值域应为y＝f(u)的定义域的子集。例如
：y＝102x-1可以看作是函数y＝10x与u＝2x-1复合而成的。
(2)y＝f［(x)］的定义域是指使得u＝(x)有意义且同时使y＝f(u)有意义的x的取值范围 。记此定义域为D，当x∈D时，u的值域为D′，当u在D′内变化时，此时y的取值集合称为 y＝f［(x)］的值域。
(3)在复合函数y＝f［(x)］中，若u＝φ(x)在区间(a,b)上是单调函数，复合函数y＝f(u)
在区间((a)， (b))或((b)，(a))上是单调函数，那么复合函数y＝f［(x)］在区间(a,b)上也一定是单调函数，它的增减性如下：当u＝(x)与y＝f(u)的增减性相同时，y ＝f［(x)］是增函数，否则为减函数。
(4)通过对函数图像的平移、对称等变换，可使函数形式变得更为简洁。
(A)y＝f(x+a)的图像：是将y＝f(x)图像左移a个单位。
(B)y＝f(x)+b的图像：是将y＝f(x)图像上移b个单位。
(C)y＝-f(x)的图像：是将y＝f(x)图像关于x轴对称而得到。
(D)y＝f(-x)的图像：是将y＝f(x)图像关于y轴对称而得到。
(E)y＝｜f(x)｜图像：是将f(x)＜0的部分曲线关于x轴对称、同时将f(x)≥0的部分曲线保 持不变。
(F)y＝f(｜x｜)的图像：是将x≥0处的图像y＝f(x)保持不变，x≤0处的图像 由y＝f(x)(x ≥0)关于y轴对称而得到。
(5)如果f(m+x)＝f(m-x)成立，则y＝f(x)图像关于x＝m对称，若f(x)＝f(2m-x)，则y＝f(x) 图像关于x＝m对称。
(6)函数y＝f(x-m)与y＝f(m-x)的图像关于x＝m对称。函数y＝f(x)与y＝f(2m-x)的图像关于x＝m对称。
(7)函数的最值问题与含参问题是两类重要题型，其覆盖面广、综合性强，对提高能力很有帮助。
(8)例题赏析：
例26 求函数y＝log0.2(2x2-x-3)的定义域与值域并讨论其单调性 。
解：设2x2-x-3＝u，则函数可以看成是y＝log0.2u与u＝2x2-x-3的复合函数。
∵2x2-x-3＞0 ∴x＜-1或x＞
∴函数定义域为｛x｜x＜-1或x＞｝
当x＜-1或x＞时，u＝2x2-x-3∈（0，+∞）
∴y∈R，即值域为R
当x＜-1时u(x)
y＝log0.2u ∴y＝log0.2u(x)
当x＞时u(x) y＝log0.2u ∴y＝log0.2
∴y＝log0.2(2x2-x-3)的递增区间是(-∞，-1)，递减区间是(，+∞)
说明：讨论复合函数的单调性，值域等均不能离开定义域，通过本题训练，使学生具备深刻认识复合函数的能力。
例27
设a＞0，a≠1，f(x)＝loga(x+)
(1)判断函数f(x)的奇偶性；
(2)求函数的反函数f-1(x)；
(3)若方程f(x)＝loga(2x+ak)有实数解，求k的取值范围。
解 ∵x+＞x+｜x｜≥0 ∴f(x)定义域为R。
设u＝x+，则u∈(0，+∞)，f(x)值域为R。
(1)f(-x)＝loga(-x+)
＝loga(x+)-1
＝-f(x)
∴f(x)是奇函数。
(2)设y＝loga(x+)，则
ay＝x+ ,a-y＝ -x
∴ay-a-y＝2x x＝(ay-a-y)
∴反函数f-1(x)＝(ax-a-x) (x∈R)
(3)由对数性质知loga(x+ )＝loga(2x+ak)
∴
∴
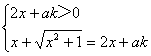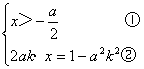
当k＝0时，②无解，从而原方程无解。
当k≠0时，又a＞0，由②得x＝
代入①得，
＞-
∴
＞0
∴
＞0 ∴k＞0
∴当k＞0时，原方程有实数解。
说明：通过讨论复合函数的性质和方程的解，训练学生解题技能和运算能力，使之具备一定综合分析能力。
例28
方程1+
有解 。求a的取值范围。
解：由题意知x＞0且x≠1且x＜2lga
整理化简原方程得：x2-2lgax+4＝0
∵Δ≥0，∴4lg2a-16≥0 ∴lga≤-2或lga≥2
∴0＜a≤
或a≥100
又x1·x2＝4＞0，x＞0
∴x1+x2＝2lga＞0
∴a＞1
故a≥100，此时 x1，2＝lga±
显然
lga-＞0 lga+＜2lga，即0＜x＜2 lga成立。若lga-＝1则lga＝
，a＝10
，此时lga+＝4是原方程的根。这就是说a≥100时，方程必有解x合条件 ：0＜x＜2lga，且x≠1。
∴方程有解时，a的取值范围是a≥100
说明：通过含参一元二次方程的讨论，训练学生对判别式及求根公式和韦达定理的综合运用 能力，使之具备正确审题，全面分析的能力。
例29
设奇函数f(x)的定义域为(-∞，0)∪(0，+∞)且在(0，+∞)上单调递增，f(1)＝0，解不等式：f［x(x-)］＜0
解：∵奇函数f(x)在(0，+∞)上递增
∴f(x)在(-∞，0)上单调递增
又f(-1)＝-f(1) ∴f(-1)＝f(1)＝0
∴当x∈(-1，0)∪(1，+∞)时f(x)＞0
当x∈（-∞，-1）∪(0，1)时 f(x)＜0
∴又x(x-)=(x-)2-
≥-＞-1欲使f〔x(x-)〕＜0成立，则必有
x·(x-)∈(0,1),即
0＜x(x-)＜1,解之得：
＜x＜0或＜x＜
说明：通过解抽象函数不等式，训练学生的逻辑思维能力使之具备分析抽象函数性质的能力。
例30 对于k∈N，用Ik表示区间(2k-1，2k+1］。已知x∈Ik时，f(x)＝(x-2k)2，求集合Mk＝｛a｜使方程f(x)＝ax在Ik上有两个不相等的实根的a的值｝
解：y＝f(x)图像就是将y＝x2(x∈（-1，1］）向右平移2k个单位所得，其中k∈N
设y1＝f(x),y2＝ax，同集合Mk可知，若a∈M，则函数y1＝f(x)与y2＝ax图像有两个交点，即当x＝2k+1时，0＜y2≤1
∴0＜a≤
∴Mk＝｛a｜0＜a≤，k∈N＝，即Mk＝(0，)
说明：通过化简集合，训练学生图像变换，数形结合能力，使之具备用图像法分析方程根的 能力。
例31 设函数y＝f(x)定义在R上，当x＞0时，f(x)＞1，且对任意m，n∈R， 有f(m+n)＝f(m)f(n)，当m≠n时，有f(m)≠f(n)
(1)证明：f(0)＝1 (2)证明：f(x)为增函数
证明：(1)令m＝0，则对任意n∈R，有
f(n)＝f(n+0)＝f(0)f(n)
∴f(0)＝1
(2)设x＜0则-x＞0且x+(-x)＝0
由(1)知 f［x+(-x)］＝1
又 f［x+(-x)］＝f(x)·f(-x),f(-x)＞1
∴f(x)＝
∈(0，1)
故当x＜0时 f(x)∈(0，1) 当x＝0时 f(x)＝1，当x＞0时f(x)＞1
即对任意x∈R，f(x)＞0成立。
设x1,x2∈R，且x1＜x2，则x2-x1＞0，x2＝x1+(x2-x1)，f(x2-x 1)＞1
f(x1)-f(x2)＝f(x1)-f［x1+(x2-x1)］＝f(x1)［1-f(x2-x1)］＜0
∴f(x1)＜f(x2)，f(x)为增函数。
说明：通过证明f(x)的单调性，训练学生讨论抽象函数f(x)性质的能力，使之具备一定的逻 辑思维能力。
【同步达纲练习】
(一)选择题
1.如右图，I是全集，M、P、S是I的3个子集，则阴影部分的集合是( )
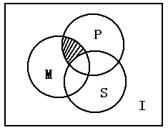
A.(M∩P)∩S
B.(B∩P)∪S
C.(M∩P)∩
D.(M∩P)∪
2.函数y=
的值域为( )
A.(-∞，)
B.(0，)
C.［，+∞］
D.［0，+∞)
3.若函数f(x)=
中，当x＜-1时，f(x)是增函数，则a的取值范围是
( )
A.a＞1 B.-1＜a＜1
C.a＞1或a＜-1 D.-1＜a＜1且a≠0
4.函数f(x)=log
(6-x-x2)的单调递增区间是( )
A.［-，+∞］
B.［-，2］
C.(-∞，-)
D.(-3，-］
5.函数y=log
(x+
+1)(x＞1 )的最大值是( )
A.-2 B.2 C.-3 D.3
6.函数y=a｜x｜(a＞1)的图像是( )
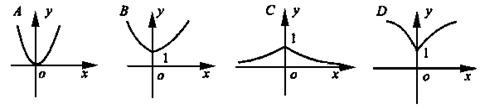
A B C D
7.已知函数f(x)存在反函数，且f(x+1)的图像过点(0，2)，那么下列函数中，可能是f(x) 的反函数的是( )
A.y=1+
(0≤x≤2)
B.y=1-(-2≤x≤2)
C.y=2-(0≤x≤2)
D.y=
(0≤x≤2)
8.设＜()b＜()a ＜1，那么( )
A.aa＜ab＜ba B.aa＜ba＜ab
C.ab＜aa＜ba D.ab＜ba＜aa
9.设f(x)是以4为周期的偶函数(x∈R)，已知x∈［0，2］时，f(x)=x
，则( )
A.f(3)＜f(
)＜f()
B.f(3)＜f()＜f()
C.f()＜f(3)＜f()
D.f()＜f(3)＜f()
10.已知
恒为正数，那么实数a的取值范围是( )
A.a＜ B. ＜a≤
C.a＞1 D. ＜a＜或a＞1
(二)填空题
11.函数y=
的定义域为
.
12.已知函数f(x)=ax+m的图像经过点(1，3)，其反函数f-1(x)的图像经过点(2，0) ，那么函数f(x)的解析式是 .
13.已知定义在闭区间［0，3］上的函数f(x)=kx2-2kx的最大值为3，那么实数k的值是 .
14.方程log2(9-2x)=3-x的解集是 .
15.如果奇函数f(x)在区间［a,b］(a,b＞0)上是增函数且有最小值3，则f(x)在区间［-b,-a ］上的最大值是 .
(三)解答题
16.求函数f(x)=
(a＞0，a≠1)的定义域.
17.已知函数f(x)=
(a≠0)的图像过点(-4，4)，且关于直线y=-x 或轴对称图形，试确定f(x)的解析式.
18.已知函数f(x)=loga(x-ka),g(x)=loga2(x2-a2)
(1)用k、a表示f(x)、g(x)的公共定义域；
(2)如果方程loga(x-ka)=loga2(x2-a2)有解；k的取值范围如何?
19.为了保护环境，实现城市绿化，某房地产公司要在拆迁地长方形ABCD上规划出一块长方 形地面建造公园，公园一边落在CD上(如图)，但不得越过文物保护区△AEF的EF.问如何设计才能使公园占地面积最大，并求这最大面积. 其中AB=200m，BC=160m，AE=60m，AF=40m.
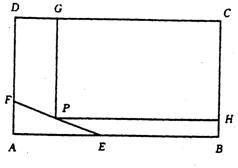
19题图
20.定义在R上的奇函数f(x)有最小正周期2，且x∈(0，1)时，f(x)=
。(1)求f(x)在［-1，1］上的解析式；(2)证明f(x)在(0，1)上是减函数；(3)当λ取何实数值时，方程f(x)=λ，在［-1，1］上有解.
参考答案
【同步达纲练习】
(一)1.C 2.B 3.D 4.B 5.A 6.B 7.A 8.C 9. D 10.D
提示：
1.了解并集、交集以及两集合互补的含义.
2.给出函数的定义域为［1，+∞)，又y=
， 故函数在［1，+∞)上是减函数，且y＞0.
3.x＜-1时，f(x)＝x2-2x-3是减函数，而f(x)是增函数，故0＜a2＜1选D.
4.函数f(x)的定义域为(-3，2).且f(x)由u=-x2-x+6与y=
复合而成.
5.当x＞1时，x++1＝(x-1)+ ]+2≥2
+2＝2+2＝4.当且仅当x-1=，即(x-1)2＝1，即x=2时，上式中等号成立，并注意y=
在(0，＋∞)上是减函数.
6.y=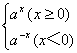
，先作y=ax(x≥0)图像，因为y=a｜x｜是偶函数，故选B.
7.f(x)的图像向左平移1个单位可得到f(x+1)的图像，故f(x+1)的图像向右平移1个单位得f (x)的图像.于是f(x+1)的图像过点(0，2)，则f(x)的图像过点(1，2)，从而f-1(x)的图像过点(2，1).依此验证可排除C、D，但B给出的函数无反函数.
8.依＜()b＜()a＜1有0＜a＜b＜1.用特殊值排除法，取a=,b=.
9.先画上函数在［0，2］上的图像，再根据周期为4和偶函数画出整个图像，然后比较大小.
10.由
或
解得.
(二) 11.［1，3］ 12.-2 13.1或-3. 14.｛0，3｝
15.
提示：
11.4-
≥0
≤4x2-4x+5≤2x2-4x+3≤01≤x≤3.
12.根据
代入f(x)求出a=2,m=1,故f(x)=2x+1.
13.f(x)=k(x2-2x)，分k=0,k＞0，k＜0讨论.
14.由原方程，得9-2x＝23-x，经变形得(2x)2-9·2x+8＝0，可解得2x=1 或2x＝8，于是x=0或x=3，并作检验而得.
15.利用函数奇偶性不难求出最大值是-3.
(三)16.由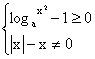
得
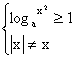于是有
当a＞1时有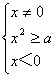
解得x≤-
；
当0＜a＜1时有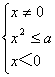
解得-≤x＜0.
因此f(x)的定义域，当a＞1时为(-∞，-)；当０＜a＜1时为［- ，0］.
17.由于(1，
)是f(x)的图像上一点，又f(x)的图像关于直线y=-x 对称，故点(-，-1)也是f(x)图像上一点，故有
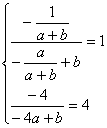可解得
因此得f(x)＝
18.(1)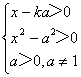
，得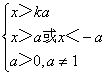
当ka＜-a即k＜-1时，ka＜x＜-a或x＞a;当-a≤ka≤a 即-1≤k≤1时，x＞a;当ka＞a即k＞1 时，x＞ka其中a＞0,a≠1。
故当k＜1时所求公共定义域为(ka,-a)∪(a,+∞)
当-1≤k≤1时所求公共定义域为(a,+∞)
当k＞时所求公共定义域为(ka,+∞)
(其中a＞0，a≠1)
(2)
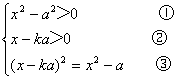
由③得x=
，代入①，②得
＞0 解得k＜-1或0＜k＜1.
19.如图所示，设PH＝x，由△FKP∽△FAE，则
，故FK＝ (200-x)，PG＝DF＝1 20+ (200-x).
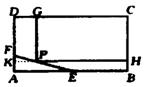
设公园占地面积为y，则
y=x〔１２０+ (200-x)〕＝-x2+
x＝-(x-190)2+×1902并且140≤x≤200.
因此当x=190时，y最大值为
.
20.(1)设x∈(-1，0)，则-x∈(0,1),又f(x)为奇函数。
所以f(x)=-f(-x)=-
=-
由f(0)=f(-0)=-f(0)f(0)=0
又f(x)的周期为2，f(1)=f(-2+1)
=f(-1)
=-f(1)f(1)
=f(-1)=0
f(0)=f(1)=f(-1)=0
故在区间［-1，1］上
f(x)=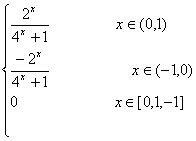
(2)设0＜x1＜x2＜1
f(x1)-f(x2)=
因为 0＜x1＜x2＜1 2x1-2x2＞0，2x1+x2-1＞0
所以 f(x1)-f(x2)＞0，即f(x1)＞f(x2)
且f(x)在(0，1)上单调递减
(3)当且仅当λ在函数y=f(x),x∈［-1,1］的值域内取值时，方程f(x)=λ在［-1，1］上有解
因为 f(x)在(0，1)上单调递减，
且 f(0)=,f(1)=
所以
＜f(x)＜ ，即f(x)∈
(，)
且 f(x)为奇函数，x∈(-1,0)时-x∈(0,1),
f(-x)∈(，)即-f(x)∈(，) ,
f(x)∈(,-)
又f(-1)=f(0)=f(1)=0
故 当λ在(，)∪(-，-)∪ ｛0｝内取值时，方程f(x)=λ在［-1,1］内有解。