离散型随机变量的分布列、期望、方差复习指导

离散型随机变量的分布列、期望、方差 复习指导

　　学习要求： 了解随机变量，离散型随机变量的意义，会求简单的离散型随机变量，掌握离散型随机变量的分布列，会求出期望、方差。
　　知识总结：
　　一、离散型随机变量的分布列
　　1.随机变量：如果一个随机试验的结果可以用一个变量来表示，这样的变量叫做随机变量，可以按一定次序列出的随机变量叫做离散型随机变量，常用ξ，等希腊字母表示
　　2.离散型随机变量的分布列 ：若离散型随机变量ξ的一切可能取值为：a₁, a₂, ……, a_n, ……, 相应取这些值的概率为：p₁，P₂，……, P_n, ……，则称下表：
　　
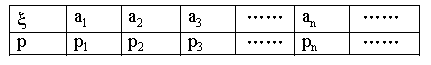
　　为离散型随机变量ξ的概率分布列，简称ξ的分布列。
　　离散型随机变量的分布列具有的两个性质： ①P_i0(i=1,2,……,n,……) 　②P₁+P₂+……+P_n+……=1
　　一种典型的离散型随机变量的分布列：
　二项分布：设重复独立地进行n次随机试验A，在每一次试验中，P(A)=P(0<P<1)，ξ为n次试验中A发生的次数，则ξ的分布列为：
　　
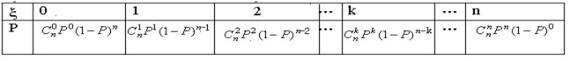
　　称ξ服从二项分布，记作ξ～B(n,P)
　　注：是二项展开式
　　[P+(1-P)]ⁿ=++……++……+
　　中的第k+1项。
　　P₁+P₂+……+P_n=++……+=[P+(1-P)]ⁿ=1。
　　二、离散型随机变量的期望与方差
　　1．期望：设离散型随机变量ξ的分布列是：

ξ	a1	a2	……	an	……
p	p1	p2	……	pn	……

称a₁p₁+a₂p₂+……+a_np_n+……为ξ的数学期望，简称期望，记作Eξ。
　　期望的性质： ①若=aξ+b (a,b均为常数), 则E=aEξ+b。

 ②E(ξ₁+ξ₂)=Eξ₁+Eξ₂。 ③若ξ～B(n, p), 则Eξ=np

　　注：期望Eξ是反映随机变量ξ集中趋势的指标，也反映了ξ取值的平均水平。
　　2．方差: 设离散型随机变量ξ的分布列是

ξ	a1	a2	……	an	……
p	p1	p2	……	pn	……

称(a₁-Eξ)²p₁+(a₂-Eξ)²p₂+……+(a_n-Eξ)²p_n+……为随机变量ξ的均方差，简称方差，记作Dξ。
　　称为随机变量ξ的标准差，记作。
　　方差的性质： 　　①D(aξ+b)=a²Dξ 　　②若ξ～B(n, p), 则Dξ=np(1-p)
　　注：方差与标准差都反映了ξ关于期望的稳定与波动、集中与离散的程度。
　　3. 期望与方差的关系： Dξ=E(ξ)^2_ (Eξ)²

例题选讲：
　　例1．设离散型随机变量ξ的分布列为：

ξ	0	1	2	3	4
P

　　分别求2ξ+1，ξ-1的分布列。
　　解：2ξ+1的分布列为：

2ξ+1	1	3	5	7	9
P

　　ξ-1的分布列为：

ξ-1	0	1	2	3
P

　　注：ξ取不同的值时，y=f(ξ)会取到相同的值，这时要考虑所有使f(ξ)=成立的ξ₁，ξ₂，……，ξ_p等值，则p()=p(f(ξ))=p(ξ₁)+p(ξ₂)+……+p(ξ_p)
　　例2．某厂生产电子元件，其产品的次品率为5%，现从一批产品中任意地连续取出2件，写出其中次品数ξ的概率分布。
　　解：由题意，得到的次品数ξ～B(2,5%)。P(ξ=0)=(95%)²=0.9025 ,P(ξ=1)=(5%)(95%)=0.095
　　　　P(ξ=2)=(5%)²=0.0025 因此，次品数ξ的概率分布为：

ξ	0	1	2
P	0.9025	0.095	0.0025

　　注：一批产品可以认为数量较大，从中任意地连续取出2件，相当于2次独立重复试验，得到的次品数ξ服从二项分布。
　　例3．设ξ的分布列为p(ξ=k)=,(k=0,1,2,……,10)，求：（1）a；（2）p(ξ≤2)；（3）p(9<ξ<20)。
　　解：（1）根据分布列的性质：p(ξ=0)+p(ξ=1)+……+p(ξ=10)=1。
　　即 a(1+)=1 　　a=。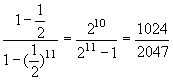
　　(2)P(ξ≤2)=P(ξ=0)+P(ξ=1)+P(ξ=2)=。
　　(3) P(9<ξ<20)=p(ξ=10)=。
　　注：分布列可有如下几种表示形式:
　　①表格，②一组等式（ξ的所有取值的概率）, ③对②进行简化表示，如本例题给出的形式。
　　例4．一批零件中有九个合格品，三个次品，安装机器时，从这批零件中随机抽取，取出的是废品则不放回，求在第一次取到合格品之前取到废品数ξ的分布列。
　　解：由题意知ξ可取0，1，2，3，则 P(ξ=0)=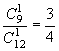 ,　P(ξ=1)=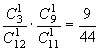
　　P(ξ=2)=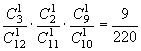。 　　P(ξ=3)=。
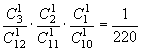　　所以ξ的分布列如下：

ξ	0	1	2	3
P

　　说明：ξ=0表示在取得合格品之前取得0个次品，确切的意义为取得的第一个零件就是合格品。解此类题的一般性原则是：上一次试验若取到一个废品，则下一次试验时，总数和废品数量都应减少一个；当取完全部废品后，下一次试验必取到合格品。
　　例5．设ξ是一个离散型随机变量，其分布列如下：

ξ	-1	0	1
P		1-2q	q2

　　求Eξ、Dξ。
　　解：根据离散型随机变量的分布列的性质，有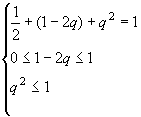： 　　， q=1-。
　　所以ξ的分布列为

ξ	-1	0	1
P		-1

∴Eξ=(-1)×+0×(-1)+1×()=1-。
　　Dξ=[-1-(1-)]²×+(1-)²×(-1)+[1-(1-)]²×()=-1。
　　注：求离散型随机变量的期望与方差，首先要明确随机变量的分布列，若分布列中的概率值为待定常数时，应先根据分布列的性质求出这些待定常数，再求其期望与方差。
　　例6．交5元钱，可以参加一次摸奖，一袋中有同样大小的球10个，其中有8个标有1元钱，2个标有5元钱，摸奖者只能从中任取2个球，他所得的奖励是所抽2球的钱数之和，求抽奖人获利的数学期望。 分析：抽到的2个球上的钱数之和ξ是个随机变量，其每一个ξ取值时所代表的随机事件的概率是容易获得的。本题的目标是求参加摸奖的人获利的数学期望，由ξ与的关系=ξ-5，利用公式E=Eξ-5可求。
　　解：设ξ为抽到的2个球钱数之和，则ξ的可能取值为：ξ=2(2个1元)
　　ξ=6（1个1元和一个5元） 　　ξ=10（2个5元）
　　所以，由题意：P(ξ=2)=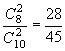。 　　P(ξ=6)= 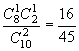　　P(ξ=10)=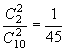
　　Eξ=。
　　设为可能的获利值，抽奖者获利的期望为：E=Eξ-5=-5=-1.4。
　　注：因为是先交5元才能参加抽奖，因此要计算E。最终E的结果为负，说明摸奖者若重复这种抽奖，平均每摸一次要亏1.4元。同学们可以自己算一下若每次允许摸3个球的情况。
　　例7．甲、乙两名工人加工同一种零件，每人每天加工的零件数相等，所得次品数分别为ξ，，ξ与的分布列如下：
　　
　　试对这两名工人的技术水平进行比较
　　分析：本题要比较的一是在加工零件数相等的条件下出次品数的平均值，即期望；二是看出次品数的波动情况，即方差值的大小。
　　解：工人甲生产出次品数ξ的期望与方差为：
　　Eξ=0×+1×+2×=0.7。 　　Dξ=(0-0.7)²×+(1-0.7)²×+(2-0.7)²×=0.891。
　　工人乙生产出次品数的期望和方差为： 　E=0×+1×+2×=0.7。
　　D=(0-0.7)²×+(1-0.7)²×+(2-0.7)²×=0.664。
可以看出，Eξ=E, 所以两人出次品的平均数相同，技术水平相当；但Dξ>D，则乙的技术比较稳定。
　　注：期望仅体现了随机变量取值的平均大小，如果两个随机变量的均值相等，还要看随机变量的取值如何在均值周围变化，即计算方差，方差大说明随机变量取值较分散，方差小说明取值分散性小或者取值比较集中、稳定。