立体几何问题的四种转化策略

立体几何问题的四种转化策略

　

　　立体几何是高中数学的一个重要内容，也是数学学习中的难点之一。在这部分中蕴含着多种数学思想方法，因而立体几何问题的解决不仅需要具有良好的空间想像能力和过硬的计算技能，还需要灵活的数学思想，其中最重要的就是转化思想。本文例说解立体几何问题常用的几种转化策略。

一、距离的转化

　　线线、线面、面面关系贯穿于立体几何始终，距离问题便是依托于这三种关系及其转化的一种重要问题。

  例1. （’89全国高考）如图，已知圆柱的底面半径是3，高为4，A、B两点分别在两底面的圆周上，并且，求直线AB与轴之间的距离。

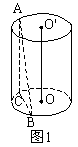
　　分析：如图1，过A作AC垂直于底面，垂足为C，连结BC，则平面ABC

　　显然两直线与AB的距离，即可转化为直线与平面ABC的距离，进而转化为O到平面ABC的距离，易得，所求距离。

　  说明：两条异面直线的距离，线面距离，点面距离。面面距离，既相互联系，又可相互转化。距离转化策略，正是解决此类问题的上策。

二、割·补转化

　　割·补转化是通过割与补，来改变几何体的状态，由复杂几何体变为简单几何体的数学方法。

  例2. （’87全国高考）如图2，三棱锥中，已知，PA、BC的公垂线段，求证三棱锥的体积。

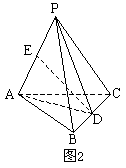
　　分析一：

　　如图2，连结AD、PD，

　　

　　平面APD，又，

　　∴

  　分析二：

　　如图3，以三棱锥的底面为底面，侧棱PA为侧棱，补成三棱柱，连结EC、EB，则易证AP⊥平面EBC，

　　

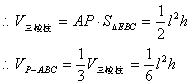
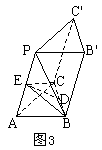
　　分析三：

　　如图4，将补成平行四边形ABCF，可利用

　　易得：

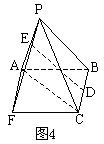
 　 说明：割·补转化是解决立体几何问题常用的方法之一，对同一几何体既可进行合理分割，又可实施有效的添补。

三、降维转化

　　由三维空间向二维空间转化，是研究立体几何问题最重要的数学方法之一。在解决实际问题中，往往通过一定手段，将空间问题转化成平面问题，得以解决。

  例3. 如图5，设正三棱锥S—ABC的底面边长为a，侧棱长为2a，过A作与侧棱SB、SC都相交的截面AEF，求这个截面周长的最小值。

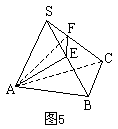
　　分析：沿侧棱SA将三棱锥的侧面展开如图6，求周长最小值问题就转化成了求A、A'两点间的最短距离。

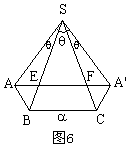
　　设，则由余弦定理得

　　所以

　　可求得

　　即所求截面周长的最小值为

 　 说明：这类问题通常都是将几何体的侧面展开，空间问题转化成平面问题来解决。

四、等积转化

　　等积转化，亦称等积变换。通常是指用不同的方式求同一几何体的体积（或同一平面图形的面积）

  例4. （’98全国高考）已知斜三棱柱，的侧面与底面垂直，且，（如图7）

　　（III）求C到侧面的距离。

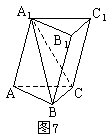
　  分析：连结A₁B、A₁C，过A₁作AC的垂线A₁D，D为垂足，由题意可知A₁D⊥面ABC。根据定义，点C到面A₁AAB₁的距离，即为三棱锥C—A₁AB的高h。

　　由得：

　　

　　即：

　　为所求

  例5. （’92全国高考）如图8，已知是棱长为a的正方体，E、F分别为棱与的中点，求四棱锥的体积。

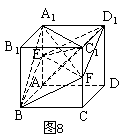
  　分析：

　　易证四边形为菱形，连结，则

　　

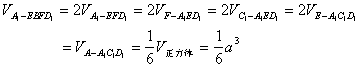
  　说明：利用等积变换既可求得有关几何体的体积，又可避开作出点到平面的距离而直接求出。

　　总之，立体几何问题联系多多，变化多多，但只要能对其进行合理而有效的转化，便可使问题浮出水面，看得见，摸得着。