利用导数判断函数的单调性的方法

利用导数判断函数的单调性的方法

利用导数判断函数的单调性，其理论依据如下：

设函数在某个区间内可导，如果，则为增函数；如果，则为减函数。如果，则为常数。

要用导数判断好函数的单调性除掌握以上依据外还须把握好以下两点：

一．　　　　　　 导数与函数的单调性的三个关系

我们在应用导数判断函数的单调性时一定要搞清以下三个关系，才能准确无误地判断函数的单调性。以下以增函数为例作简单的分析，前提条件都是函数在某个区间内可导。

1．与为增函数的关系。

由前知，能推出为增函数，但反之不一定。如函数在上单调递增，但，∴是为增函数的充分不必要条件。

2．时，与为增函数的关系。

若将的根作为分界点，因为规定，即抠去了分界点，此时为增函数，就一定有。∴当时，是为增函数的充分必要条件。

3．与为增函数的关系。

由前分析，为增函数，一定可以推出，但反之不一定，因为，即为或。当函数在某个区间内恒有，则为常数，函数不具有单调性。∴是为增函数的必要不充分条件。

函数的单调性是函数一条重要性质，也是高中阶段研究的重点，我们一定要把握好以上三个关系，用导数判断好函数的单调性。因此新教材为解决单调区间的端点问题，都一律用开区间作为单调区间，避免讨论以上问题，也简化了问题。但在实际应用中还会遇到端点的讨论问题，特别是研究以下问题时。

二．函数单调区间的合并

函数单调区间的合并主要依据是函数在单调递增，在单调递增，又知函数在处连续，因此在单调递增。同理减区间的合并也是如此，即相邻区间的单调性相同，且在公共点处函数连续，则二区间就可以合并为一个区间。

【例】用导数求函数（）的单调区间。

解：（用第一种关系及单调区间的合并），当，即或时，∴在，上为增函数，又∵在处连续，且相邻区间的单调性又相同，∴在上为增函数。

旧教材很少提到函数单调区间的合并，原因在于教师很难讲，学生很难把握，但是新教材引进函数的连续性和导数之后就很容易说明，也很容易理解了。

综之，用导数证明划分函数的单调性是导数最常用、也是最基本的应用，其它重要性如极值、最值等都必须用到单调性。它比用单调性的定义证明要简单许多，划分也容易理解得多。讨论可导函数得单调性可按如下步骤进行：

（1）　　　 确定的定义域；（2）求，令，解方程求分界点；

（3）用分届点将定义域分成若干个开区间；

（4）判断在每个开区间内的符号，即可确定的单调性。

以下是前几年高考用导数证明、求单调性的题目，举例说明如下：

例1设，是上的偶函数。

（I）求的值；（II）证明在上是增函数。（2001年天津卷）

解：（I）依题意，对一切有，即，

∴对一切成立，由此得到，，又∵，∴。

（II）证明：由，得，

当时，有，此时。∴在上是增函数。

例2设函数，其中。（2000年全国、天津卷）

（I）解不等式；（II）证明：当时，函数在区间上是单调函数。

解1：（I）分类讨论解无理不等式（略）。 （II）作差比较（略）。

解2：（i）当时，有，此时，函数在区间上是单调递减函数。但，因此，当且仅当时，。

（ii）当时，解不等式，得，在区间上是单调递减函数。解方程，得或，

∵，　∴当且仅当时，，

综上，（I）当时，所给不等式的解集为：；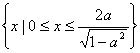

当时，所给不等式的解集为：。

（II）当且仅当时，函数在区间上时单调函数。

例3设，求函数的单调区间。（2003年高考（理）19题）

解：（）　 当，时，

，，

（i）当时，对所有，恒有，即，此时在单调递增；

（ii）当时，对，恒有，即，此时在单调递增，在单调递增，

又知函数在处连续，因此在单调递增；

（iii）当时，令，即，

解得或，因此，函数在单调递增，在单调递增，令，即，

解得，

因此，函数在上单调递减。

本题用传统作差比较法无法求函数的单调区间，只有用导数才行。