|
|
学科:数学 |
| 教学内容:第六章 排列组合、二项式定理 |
一、考纲要求
1.掌握加法原理及乘法原理,并能用这两个原理分析解决一些简单的问题.
2.理解排列、组合的意义,掌握排列数、组合数的计算公式和组合数的性质,并能用它们解 决一些简单的问题.
3.掌握二项式定理和二项式系数的性质,并能用它们计算和论证一些简单问题.
二、知识结构

![]()
三、知识点、能力点提示
(一)加法原理、乘法原理
说明 加法原理、乘法原理是学习排列组合的基础,掌握此两原理为处理排 列、组合中有关问题提供了理论根据.
例1 5位高中毕业生,准备报考3所高等院校,每人报且只报一所,不同的 报名方法共有多少种?
解: 5个学生中每人都可以在3所高等院校中任选一所报名,因而每个学生都有3种不同的 报名方法,根据乘法原理,得到不同报名方法总共有
3×3×3×3×3=35(种)
(二)排列、排列数公式
说明 排列、排列数公式及解排列的应用题,在中学代数中较为独特,它研 究的对象以及研 究问题的方法都和前面掌握的知识不同,内容抽象,解题方法比较灵活,历届高考主要考查 排列的应用题,都是选择题或填空题考查.
例2 由数字1、2、3、4、5组成没有重复数字的五位数,其中小于50 000的 偶数共有( )
A.60个 B.48个 C.36个 D.24个
解 因为要求是偶数,个位数只能是2或4的排法有P12;小于50 000的五位数,万位只能是1、3或2、4中剩下的一个的排法有P13;在首末两位数排定后,中间3个位数的排法有P33,得P13P33P12=36(个)
由此可知此题应选C.
例3 将数字1、2、3、4填入标号为1、2、3、4的四个方格里,每格填一个 数字,则每个方格的标号与所填的数字均不同的填法有多少种?
解: 将数字1填入第2方格,则每个方格的标号与所填的数字均不相同的填法有3种,即214 3,3142,4123;同样将数字1填入第3方格,也对应着3种填法;将数字1填入第4方格,也对 应3种填法,因此共有填法为
3P13=9(种).
(三)组合、组合数公式、组合数的两个性质
说明 历届高考均有这方面的题目出现,主要考查排列组合的应用题,且基本上都是由选择题或填空题考查.
例4 从4台甲型和5台乙型电视机中任意取出3台,其中至少有甲型与乙型电 视机各1台,则不同的取法共有( )
A.140种 B.84种 C.70种 D.35种
解: 抽出的3台电视机中甲型1台乙型2台的取法有C14·C25种;甲型2台乙型1台 的取法有C24·C15种
根据加法原理可得总的取法有
C24·C25+C24·C15=40+30=70(种 )
可知此题应选C.
例5 甲、乙、丙、丁四个公司承包8项工程,甲公司承包3项,乙公司承包1 项,丙、丁公司各承包2项,问共有多少种承包方式?
解: 甲公司从8项工程中选出3项工程的方式 C38种;
乙公司从甲公司挑选后余下的5项工程中选出1项工程的方式有C15种;
丙公司从甲乙两公司挑选后余下的4项工程中选出2项工程的方式有C24种;
丁公司从甲、乙、丙三个公司挑选后余下的2项工程中选出2项工程的方式有C22种.
根据乘法原理可得承包方式的种数有![]() ×C15×C24×C22=
×C15×C24×C22=![]() ×1=1680(种).
×1=1680(种).
(四)二项式定理、二项展开式的性质
说明 二项式定理揭示了二项式的正整数次幂的展开法则,在数学中它是常用的基础知识 ,从1985年至1998年历届高考均有这方面的题目出现,主要考查二项展开式中通项公式等, 题型主要为选择题或填空题.
例6 在(x-![]() )10的展开式中,x6的系数是( )
)10的展开式中,x6的系数是( )
A.-27C610 B.27C410 C.-9C610 D.9C410
解 设(x-![]() )10的展开式中第γ+1项含x6,
)10的展开式中第γ+1项含x6,
因Tγ+1=Cγ10x10-γ(-![]() )γ,10-γ=6,γ=4
)γ,10-γ=6,γ=4
于是展开式中第5项含x6,第5项系数是C410(-![]() )4=9C410
)4=9C410
故此题应选D.
例7 (x-1)-(x-1)2+(x-1)3-(x-1)4+(x-1)5的展开式中的x2的 系数等于
解:此题可视为首项为x-1,公比为-(x-1)的等比数列的前5项的和,则其和为
![]()
在(x-1)6中含x3的项是C36x3(-1)3=-20x3,因此展开式中x2的系数是-2 0.
(五)综合例题赏析
例8 若(2x+![]() )4=a0+a1x+a2x2+a3x3+a4x4,则(a0+a2+a4)2-(a1+a3)2的值为( )
)4=a0+a1x+a2x2+a3x3+a4x4,则(a0+a2+a4)2-(a1+a3)2的值为( )
A.1 B.-1 C.0 D.2
解:A.
例9 2名医生和4名护士被分配到2所学校为学生体检,每校分配1名医生和2 名护士,不同的分配方法共有( )
A.6种 B.12种 C.18种 D.24种
解 分医生的方法有P22=2种,分护士方法有C24=6种,所以共有6×2=12种不同 的分配方法。
应选B.
例10 从4台甲型和5台乙型电视机中任意取出3台,其 中至少要有甲型与乙型电视机各1台,则不同取法共有( ).
A.140种 B.84种 C.70种 D.35种
解:取出的3台电视机中,甲型电视机分为恰有一台和恰有二台两种情形.
∵C24·C15+C25·C14=5×6+10×4=70.
∴应选C.
例11 某小组共有10名学生,其中女生3名,现选举2 名代表,至少有1名女生当选的不同选法有( )
A.27种 B.48种 C.21种 D.24种
解:分恰有1名女生和恰有2名女生代表两类:
∵C13·C17+C23=3×7+3=24,
∴应选D.
例12 由数学0,1,2,3,4,5组成没有重复数字的 六位数,其中个位数字小于十位数字的共有( ).
A.210个 B.300个
C.464个 D.600个
解:先考虑可组成无限制条件的六位数有多少个?应有P15·P55=600个.
由对称性,个位数小于十位数的六位数和个位数大于十位数的六位数各占一半.
∴有![]() ×600=300个符合题设的六位数.
×600=300个符合题设的六位数.
应选B.
例13 以一个正方体的顶点为顶点的 四面体共有( ).
A.70个 B.64个
C.58个 D.52个
解:如图,正方体有8个顶点,任取4个的组合数为C48=70个.
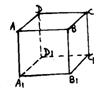
其中共面四点分3类:构成侧面的有6组;构成垂直底面的对角面的有2组;形如(ADB1C1 )的有4组.
∴能形成四面体的有70-6-2-4=58(组)
应选C.
例14 如果把两条异面直线看成“一对”,那么六棱 锥的棱所在的12条直线中,异面直线共有( ).
A.12对 B.24对
C.36对 D.48对
解:设正六棱锥为O—ABCDEF.
任取一侧棱OA(C16)则OA与BC、CD、DE、EF均形成异面直线对.
∴共有C16×4=24对异面直线.
应选B.
例15 正六边形的中心和顶点共7个点,以其中三个点 为顶点的三角形共 个(以数字作答).
解:7点中任取3个则有C37=35组.
其中三点共线的有3组(正六边形有3条直径).
∴三角形个数为35-3=32个.
例16 设含有10个元素的集合的全部子集数为S,其中由3个元素组成的子集 数为T,则![]() 的值为
。
的值为
。
解 10个元素的集合的全部子集数有:
S=C010+C110+C210+C310+C410+C510+C610+C710+C810+C910+C1010=210=1024
其中,含3个元素的子集数有T=C310=120
故![]() =
=![]()
例17 在50件产品 n 中有4件是次品,从中任意抽了5件 ,至少有3件是次品的抽法共 种(用数字作答).
解:“至少3件次品”即“有3件次品”或“有4件次品”.
∴C34·C246+C44·C146=4186(种)
例18 有甲、乙、丙三项任务,甲需2人承担,乙、 丙各需1人承担,从10人中选派4人承担这三项任务,不同的选法共有( ).
A.1260种 B.2025种
C.2520种 D.5040种
解:先从10人中选2个承担任务甲(C210)
再从剩余8人中选1人承担任务乙(C18)
又从剩余7人中选1人承担任务乙(C17)
∴有C210·C18·C17=2520(种).
应选C.
例19 集合{1,2,3}子集总共有( ).
A.7个 B.8个 C.6个 D.5个
解 三个元素的集合的子集中,不含任何元素的子集有一个,由一个元素组成的子集数
C13,由二个元素组成的子集数C23。
由3个元素组成的子集数C33。由加法原理可得集合子集的总个数是
C13+C23+C33+1=3+3+1+1=8
故此题应选B.
例20 假设在200件产品中有3件是次品,现在从中任意抽取5件,其中至少有两件次品的抽法有( ).
A.C23C3197种 B.C23C3197 +C33C2197
C.C5200-C5197 D.C5200-C 13C4197
解:5件中恰有二件为次品的抽法为C23C3197,
5件中恰三件为次品的抽法为C33C2197,
∴至少有两件次品的抽法为C23C3197+C33C2197.
应选B.
例21 两排座位,第一排有3个座位,第二排有5个座位,若8名学生入座(每人一个座位),则不同座法的总数是( ).
A.C58C38 B.P12C58C38
C.P58P38 D.P88
解:对于8个人的任意一个排列均可“按先前排从左到右再后排从左到右”的次序入座.
∴应有P88种不同的入座法.
应选D.
例22 7人并排站成一行,如果甲、乙必须不相邻,那么不同排法的总数是 ( ).
A.1440 B.3600 C.4320 D.4800
解:7人的全排列数为P77.
若甲乙必须相邻则不同的排列数为P22P66.
∴甲乙必须不相邻的排列数为P77-P22P66=5P66=3600.
应选B.
例23 用1,2,3,4,四个数字组成没有重复的四位奇数的个数是 个(用具体数字作答).
解:末位数(C12),前三位数(P33).
∴有C12P33=12个四位奇数.
例24 用1,2,3,4,四个数字组成的比1234大的数共有 个(用具体 数字作答).
解:若无限制,则可组成4!=24个四位数,其中1234不合题设.
∴有24-1=23个符合题设的数.
例25 用0,1,2,3,4这五个数字组成没有重复数字的四位数,那么在这些 四位数中,是偶数的总共有( ).
A.120个 B.96个 C.60 个 D.36个
解:末位为0,则有P34=24个偶数.
末位不是0的偶数有P12P13P23=36个.
∴共有24+36=60个数符合题设.
应选C.
例26 已知集合A和集合B各含有12个元素,A∩B含4个元素,试求同时满足下面两个条件的集合C的个数:
(1)C![]() A∪B,且C中含有3个元素;
A∪B,且C中含有3个元素;
(2)C∩A≠![]() (
(![]() 表示空集).
表示空集).
解:∵A∪B含有12+12-4=20个元素;
B含12个元素,
∴![]() ∩B含20-12=8个元素,
∩B含20-12=8个元素,
若C中恰含A中1个元素,则有C112·C28个,
若C中恰含A中2个元素,则有C212·C28·C28个,
若C中恰含A中3个元素,则有C312个,
∴符合题设的集合C的个数为
C112C28+C212C18+C312=1084个.
例27 四面体的顶点和各棱中点共10个点,在其中取4 个不共面的点,不同的取法共有( )
A.150种 B.147种 C.144种 D.141种
解:从10点中任取4点的组合数为C410=210.
其中有4·C46=60组点,每组中的四点恰为一个侧面上的点.
其中任取同一棱上3点它们和相对棱的中点共面,即有6组这种情况应排除.
其中还有底面两棱中点和对面两棱中点共面,即有3组这种情况应排除.
∴符合题设的取法有150-6-3=141种.
应选D.
例28 已知(![]() )9的展开式中x3的系数为
)9的展开式中x3的系数为![]() ,常数a的值为
.
,常数a的值为
.
解:Tk+1=Ck9(![]() )9-k(
)9-k(![]() )k
)k
=Ck9·a9-k2![]() ·xk-9+
·xk-9+![]()
令k-9+![]() =3,得k=8,
=3,得k=8,
∴x3的系数为C89·a·2-4=![]() .
.
即![]() a=
a=![]() ,得a=4.
,得a=4.
例29 (![]() )6的展开式中的常数项为( )
)6的展开式中的常数项为( )
A.-160 B.-40 C.40 D.160
解:Tk+1=Ck6(![]() )6-k(-
)6-k(-![]() )k
)k
=Ck6·(-2)k·x![]()
令![]() =0,得k=3
=0,得k=3
∴常数项为C36·(-2)3=-160
应选A.
例30 若(![]() )n展开式 中前三项系数成等差数列,求出展开式里的有理项。
)n展开式 中前三项系数成等差数列,求出展开式里的有理项。
解 由于展开式前三项系数成等差数列
所以 2C1n(![]() )=C0n+C2n(
)=C0n+C2n(![]() )2,n=1+
)2,n=1+![]()
解方程得n=9或n=1(舍去)
又展开式的通项为
Tγ+1=Cγ8(x![]() )8-γ
)8-γ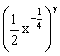
![]() X
X![]() =Cγ8(
=Cγ8(![]() )γx
)γx![]()
因0≤4-![]() ≤8,且4-
≤8,且4-![]() 是整数。
是整数。
所以γ是4的倍数。
取γ=0或γ=4
故(![]() )8展开式中第一项和第五项为有理 项,其有理项为
)8展开式中第一项和第五项为有理 项,其有理项为
T1=C08x4=x4
T5=C48(![]() )4(x4-3)=
)4(x4-3)=![]() ×
×![]()
例31 (x+2)10(x2-1)的展开式中x10 的系数是 (用数字作答)。
解 因(x+2)10展开式中x10的系数是1,x8的系数为C21022=180 ,所以(x+2)10(x2-1)的展开式中,x10的系数为180-1=179
例32 9192除以100的余数 .
解:9192=(100-9)92≡992(mod 100).
992=(10-1)92=1092-…+C9092·100-C919210+1
≡ -C9192·10+1(mod 100)
-C9192·10+1=-920+1=-919≡-19(mod 100),
-19≡81 (mod 100).
∴9192除以100的余数是81.
例33 由(![]() )100的展开所得的x的多项式中,系数为有理数的共有( )
)100的展开所得的x的多项式中,系数为有理数的共有( )
A.50项 B.17项 C.16项 D.15项
解:Tk+1=Ck10(![]() x)10-k(
x)10-k(![]() )k
)k
=Ck10·(![]() )10-k(
)10-k(![]() )k(x)10-k(k=0,1,2,…,100)
)k(x)10-k(k=0,1,2,…,100)
由![]() ∈N,
∈N,![]() ∈N,k∈{0,1,2,…,100},得
∈N,k∈{0,1,2,…,100},得
k=0,6,12,18,…,96,共17项.
∴应选B.
例34 在(3-x)7的展开式中,x5的系数是 (用数字作答).
解:Tk+1=Ck7·37-k·(-x)k=Ck7·(-1)k·xk,
∴T6=C57·37-5·(-1)5x5=-189x5.
即x5的系数是-189.
例35 在(1-x3)(1+x)10的展开式中,x5的系数是( ).
A.-297 B.-252 C.297 D.207
解:(1-x3)(1+x)10
=(1-x3)(…+C550x5+…+C210x2+…)
∴x5的系数为+C550-C210=207.
应选D.
例36 求(2x3-![]() )15的展开式的常数项.
)15的展开式的常数项.
解:Tk+1=Ck5·(2x3)5-k·(-![]() )k=(-1)k ·Ck5·25-k·x15-3k-2k
)k=(-1)k ·Ck5·25-k·x15-3k-2k
令15-5k=0,得k=3
∴常数项为T4=(-1)3·C35·25-3=-40.
例37 在(x-![]() )8的展开式中,x4的系数与
)8的展开式中,x4的系数与![]() 的系数之差是
.
的系数之差是
.
解:Tk+1=Ck8·(-x)8-k·(-![]() )k=Ck8·(-1)k·x8-k-k.
)k=Ck8·(-1)k·x8-k-k.
令8-2k=-4,得k=6,![]() 得k=2,
得k=2,
∴T7=C68·(-1)6![]() =28·
=28·![]() .
.![]()
∴x4与![]() 的系数之差是28-28=0.
的系数之差是28-28=0.
例38 已知(x+a)7的展开式中,x4的系数是-280,则a= .
解:T4=C37·x4a3=C37a3x4.
由已知C37a3=-280![]() 35a3=-280,得a=-2.
35a3=-280,得a=-2.
例39 在(1-x2)20的展开式中,如果第4r项和第r+2项的二项式系数 相等,
(1)求r的值;
(2)写出展开式中的第4r项和第r+2项.
解:(1)第4r项和第r+2项的二项式系数分别是![]() 和
和![]()
![]() =
=![]()
![]() 4r-1=r+1或4r-1+r+1=20,
4r-1=r+1或4r-1+r+1=20,
得r=4和r=![]() (舍去)
(舍去)
∴r=4
(2)T4r=T16=C1520·(-x2)15=-15504x30,
Tr+2=T6=C520(-x2)5=-15504x10
例40 在(1+x+x2)(1-x)10的展开式中,x5的系数是 (用具体数字作答).
解:(1+x+x2)(1-x)10
=(1+x+x2)(1-1x+45x2-120x3+210x4-252x5+…)
=…+(-120+210-252)x5+….
∴x5的系数是-120+210-252=-162.
例41 已知(1-2x)7=a0+a1x+a2x2+…+a7x7;那么a1+a2+ …+a7= .
解:令x=1,代入已知式,得-1=a0+a1+…+a7,
将x=0代入已知式,得1=a0
∴a1+a2+…+a7=-1-a0=-2.
例42 如果n是正偶数,则C0n+C2n+C4n+…+Cn-2n+Cnn=( ).
A.2n B.2n-1 C.2n-2 D.(n-1)2n-1 E.(n-1)2n-2
解:∵C0n+C2n+…+Cn-2n+Cnn=C1n+C3n+…+Cn-1n ,
又(C0n+C2n+…+Cn-2n+Cnn)+(C1n+C3n+…+Cn-1n)= 2n,
∴2(C0n+C2n+…+Cn-2n+Cnn)=2n,
C0n+C2n+…+Cn-2n+Cnn=2n-1.
应选B.

【同步达纲练习】
四、能力训练
(一)选择题
1.有多少个整数n能使(n+i)4成为整数( )
A.0 B.1 C.2 D.3
(2)已知(ax+1)2n和(x+a)2n+1的展开式中含xn项的系数相同(a≠0为实数,n ∈N),则a的取值范围是( )
A.a=1 B.a>1 C.a< 1 D.a≥1
3.在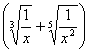 n的展开式中,所有奇数项二项式系数之和等于1024,则中间项
的二项式系数是(
)
n的展开式中,所有奇数项二项式系数之和等于1024,则中间项
的二项式系数是(
)
A.330 B.462 C.682 D.792
4.在(![]() )8的展开式中的常数项是 ( )
)8的展开式中的常数项是 ( )
A.7 B.-7 C.28 D.-28
5.n∈N,A=(![]() +2)2n+1,B为A的小数部分,则AB的值应是( )
+2)2n+1,B为A的小数部分,则AB的值应是( )
A.72n+1 B.22n+1 C.32n+1 D.52n+1
6.某小组有8名学生,从中选出2名男生,1名女生,分别参加数、理、化单科竞赛,每人参 加一种,共有90种不同的参赛方案,则男女生的人数应是( )
A.男生6名,女生2名 B.男生5名,女生3名
C.男生3名,女生5名 D.男生2名,女生5名
7.从0,1,2,3,4中每次取出3个不同的数字组成三位数,则这些三位数的个位数字之和等 于( )
A.80 B.90 C.110 D .120
8.从集合{1,2,3,……10}中,选出由5个数组成的子集,使得这5个数中的任何两个数 的和不等于11,则这样的子集共有( )
A.10个 B.16个 C.20个 D.32个
9.设有编号为1,2,3,4,5的五个球和编号为1,2,3,4,5的五个盒子,现将这5个球投 放在这5个盒内,要求每个盒内投放一个球,并且恰有两个球的编号与盒子的编号相同,则 这样的投放方法的总数为( )
A.20 B.30 C.60 D. 120
10.用0,1,2,3,4,5,6这7个数字排成一个数字不重复且个位数最大,十位数次之,百 位数最小的三位数的个数是( )
A.10 B.20 C.30 D. 40
11.要排一张5个独唱节目和3个合唱节目的演出节目表,如果合唱节目不排头,并且任何两 个合唱节目不相邻,则不同排法的种类是( )
A.P88 B.P55·P33 C.P55·P35 D.P55·P38
12.3人坐在一排8个座位上,若每人左右两边都有空座位,则坐法种数是( )
A.12 B.6 C.24 D. 120
13.设A,B分别为(1+x)n展开式中的奇数项之和及偶数项之和,那么A2-B2的值为( )
A.(1+x)2n B.(1+x)n
C.-(1-x2)n D.不是以上结果
14.(2x+![]() )2n的展开式中,x2的系数是224,则
)2n的展开式中,x2的系数是224,则![]() 的系数是( )
的系数是( )
A.14 B.28 C.56 D.112
15.在(![]() )n的展开中,倒数第三项的系数的绝对值是45,则展形式中a2项的系数是( )
)n的展开中,倒数第三项的系数的绝对值是45,则展形式中a2项的系数是( )
A.120 B.-120 C.210 D.-210
(二)填空题
16.n是正奇数,则7n+7n-1C1n+7n-2C2n+7Cn-1n除以9的余 数是 .
17.今天是星期日,从今天起21991天后的第一天是星期 .
18.满足C7x<C5x的所有自然数x的和等于 .
19.1.0096精确到0.001的近似值是 .
(三)解答题
20.在10个数-9,-7,-5,-1,0,2,4,6,8中任取两个数构成虚数a+bi (a≠b),
求(1) 这样不同的虚数有多少个?
(2)有多少个辐角主值θ∈(![]() ,π)的 不同虚数?
,π)的 不同虚数?
(3)有多少个模大于5的不同虚数.
21.将数字0,1,2,3,5组成没有重复数字的五位偶数,按从小到大次序排列,那么第25个数是什么?
22.证明9·32n-8n-9能被64整除(n∈N).
23.设(2-![]() x)100=a0+a1x+a2x2+……+a100x100, 求(a0+a2+a4+……+a100)2-(a1+a3+a5+……+a99)2的值.
x)100=a0+a1x+a2x2+……+a100x100, 求(a0+a2+a4+……+a100)2-(a1+a3+a5+……+a99)2的值.
24.若(![]() )n展开式的二项式 系数中第二、第三、第四项的系数成一个等差数列,且展开式第六项是21,求x.
)n展开式的二项式 系数中第二、第三、第四项的系数成一个等差数列,且展开式第六项是21,求x.

参考答案
【同步达纲练习】
(一)1.B 2.A 3.B 4.A 5.C 6.C 7.B 8.D 9.A 10.B 11.C 12.C 13.C 14.A 15.C
(二)16.7 17.四 18.45 19.1.055
(三)20.(1)81,(2)20,(3)64 21.32150 22.略 23.1 24.x=0
