高三质量调查数学试题（理）
本试卷分第I卷（选择题）和第II卷（非选择题）两部分，共150分。考试时间：120分钟。
第Ⅰ卷（选择题 共60分）
一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.）
1．准线方程为
的抛物线的标准方程为 （ ）
A．
B．
C．
D．
2．函数
是 （ ）
A．最小正周期为π的奇函数 B．最小正周期为π的偶函数
C．最小正周期为2π的奇函数 D．最小正周期为2π的偶函数
3．已知向量
平行，则m等于 （ ）
A．－2 B．2 C．
D．
4．
是直线
垂直的 （ ）
A．充分而不必要的条件 B．必要而不充分的条件
C．充要条件 D．既不充分又不必要的条件
5．已知直线a、b与平面α，给出下列四个命题
①若a∥b，b
α，则a∥α; ②若a∥α，bα，则a∥b ;
③若a∥α，b∥α，则a∥b; ④a⊥α，b∥α，则a⊥b.
其中正确的命题是 （ ）
A．①和② B．①和④ C．③和④ D．只有④
6．同时抛掷4枚均匀的硬币80次，设4枚硬币正好出现2枚正面向上，2枚反面向上的次数为ξ，则ξ的数学期望是 （ ）
A．20 B．25 C．30 D．40
7．函数
的单调递增区间是 （ ）
A．
B．
C．
D．
8．已知函数
的最小值是 （ ）
A．2 B．
C．
D．
9．数列
是公差不为0的等差数列，且
是等比数列{
}的连续三项，若等比数列{}的首项
，则b2等于 （ ）
A．
B．5 C．2 D．
10．若双曲线
的左支上一点P（a，b）到直线
的距离为
+b的值为 （ ）
A．
B． C．－2 D．2
11．若一个四面体由长度为1，2，3的三种棱所构成，则这样的四面体的个数是 （ ）
A．2 B．4 C．6 D．8
12．某债券市场常年发行三种债券，A种面值为1000元，一年到期本息和为1040元；B种贴水债券面值为1000元，但买入价为960元，一年到期本息和为1000元；C种面值为1000元，半年到期本息和为1020元. 设这三种债券的年收益率分别为a, b, c，则a, b, c的大小关系是 （ ）
A．
B．
C．
D．
第Ⅱ卷（非选择题共90分）
二、填空题：（本大题共4小题，每小题4分，共16分，把答案直接填在题中横线上.）
13．已知
为虚数单位），则z=
.
14．学校组织3名同学去4个工厂进行社会实践活动，其中工厂A必须有同学去实践，每个同学去哪个工厂可自行选择，则不同的分配方案共有 种（用数字作答）.
15．已知
分别为△ABC的三边，且
.
16．已知下列四个函数：①
②
③
④
.其中图象不经过第一象限的函数有
.（注：把你认为符合条件的函数的序号都填上）
三、解答题：（本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤）.
17．（本小题满分12分）
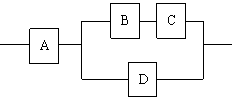如图：用A、B、C、D四类不同的元件连接成系统N，当元件A正常工作且元件B、C都正常工作，或当元件A正常工作且元件D正常工作时，系统N正常工作.已知元件A、B、C、D正常工作的概率依次为
（Ⅰ）求元件A不正常工作的概率；
（Ⅱ）求元件A、B、C都正常工作的概率；
（Ⅲ）求系统N正常工作的概率.
18．（本小题满分12分）
设
的不等式
19．（本小题满分12分）
如图：已知四棱锥P—ABCD的底面为直角梯形，AD∥BC，∠BCD=90，PA=PB，PC=PD.
（Ⅰ）证明CD与平面PAD不垂直；
（Ⅱ）证明平面PAB⊥平面ABCD；
（Ⅲ）如果CD=AD+BC，二面角P—BC—A等于60°，求二面角P—CD—A的大小.
 |
20．（本小题满分12分）
已知两点M（0，2），N（0，－2）且点P到这两点的距离的和等于6.
（Ⅰ）求动点P的轨迹方程；
（Ⅱ）若A、B是动点P的轨迹上的两点，且M分有向线段
所成的比为2，求线段
AB所在直线的方程.
21．（本小题满分12分）
用总长44.8m的钢条制做一个底面是等腰三角形的直三棱柱容器的框架，如果所制做容器的底面的腰长比底边长的一半长1m，那么底面的底边，腰及容器的高为多少时容器的容积最大？（参考数据2.662=7.0756，3.342=11.1556）
22．（本小题满分14分）
已知一次函数
的图象关于直线
对称的图象为C，且
若点
*）在曲线C上，并有
.
（Ⅰ）求的解析式及曲线C的方程；
（Ⅱ）求数列{
}的通项公式；
（Ⅲ）设
的值.