高三质量调查数学试题（理）参考答案及评分标准
一、选择题：（每小题5分，共60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | A | C | A | D | C | B | D | B | A | B | C |
二、填空题：（每小题4分，共16分）
13．
14．37 15．
16．①，④（多填少填均不给分）
三、解答题（共74分，以下为累计得分，其他解法请相应给分）
17．解：（Ⅰ）元件A正常工作的概 率P（A）=
，它不正常工作的概率
（2分）=
（3分）
（Ⅱ）元件A、B、C都正常工作的概率P(A·B·C)=P（A）P（B）P（C）（5分）
（Ⅲ）系统N正常工作可分为A、B、C都正常工作和A、D正常工作但B、C不都正常工作两种情况，前者概率
，（7分）后者的概率为
（10分）
，
所以系统N正常工作的概率是
18．解：化为
（Ⅰ）当
（Ⅱ）当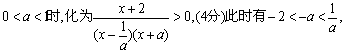
解集为
|
|
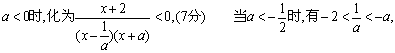
解集为
(iii)
解集为
19．（Ⅰ）若CD⊥平面PAD（1分） 则CD⊥PD（2分），由已知PC=PD，
得∠PCD=∠PDC<90°，这与CD⊥PD矛盾，所以CD与平面PAD不垂直.（3分）
（Ⅱ）取AB、CD的中点E、F联结PE、PF、EF（4分），由PA=PB，PC=PD，
得PE⊥AB，PF⊥CD.（5分）∵EF为直角梯形的中位线，∴EF⊥CD，又PF∩EF=F，∴CD⊥平面PEF，（6分）由PE
平面PEF，得CD⊥PE，又AB⊥PE且梯形两腰AB、CD必相交，∴PE⊥平面ABCD（7分）又PE平面PAB，∴平面PAB⊥平面ABCD.（8分）
（Ⅲ）由（Ⅱ）及二面角定义知∠PFE为二面角P—CD—A的平面角.（9分）作EG⊥BC于G，连PG，由三垂线定理得BC⊥PG，故∠PGE为二面角P—BC—A的平面角.（10分）即∠PGE=60°.由已知，得EF=
（AD+BC）=CD，又EG=CF=CD. ∴EF=EG，易证得Rt△PEF≌Rt△PEG.（11分）∴ PFE=∠PGE=60°，即为所求.（12分）
20．解（Ⅰ）∵MN=4，又6>4，∴点P的轨迹是椭圆（1分）
点P的轨迹方程是
（Ⅱ）设A点在B点的左方，且
即
①，又焦点M（0，2）相应的准线方程是
A到准线距离
B到准线距离
（6分），
由
于是
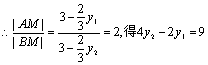
②与①联立解得
代入椭圆方程得
直线AB的斜率
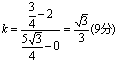，AB的方程为
（10分）如果点A在B的右方时，根据对称性，则所求的直线AB的方程为
.（12分）
21．解：设容器底面等腰三角形的底边长为2xm，则腰长为
（1分）高为
（2分）设容器的容积为Vm3，底面等腰三角形底边
上的高
令
（8分）
当
有最大值.（9分）
这时容器的底面等腰三角形的底边长为6m，腰长为4m，容器的高为5.6m.（12分）
22．解（Ⅰ）设
（2分）
即
①又
是曲线C的解析式（3分），
因为点
在曲线C上，所以
，
又
代入①得
曲线C的方程是
（Ⅱ）由（Ⅰ）知当
时，
于是
（10分）
（Ⅲ）因为
所以
（13分）
所以