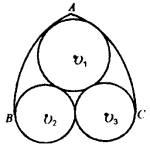
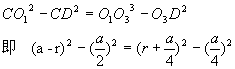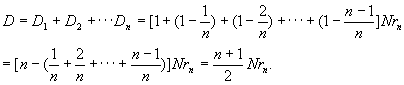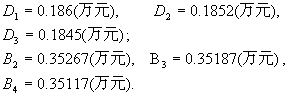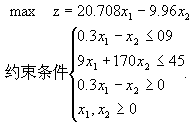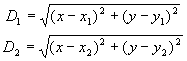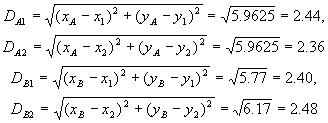| 试 题 一、窗户造型(满分15分) 《中学生数学》杂志2000年第一期的封面是一幅欧洲教堂的照片,它是一座哥特式的建筑。建筑物上有一个窗户的造型如下图所示。图中弧AB和弧AC分别是以C和B为圆心BC长为半径的圆弧.☉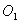 、☉ 、☉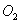 和☉ 和☉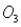 两两相切,并且☉ 两两相切,并且☉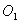 、☉ 、☉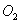 与弧AB相切, ☉ 与弧AB相切, ☉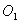 、 ☉ 、 ☉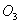 与弧 AC相切,☉ 与弧 AC相切,☉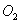 、☉ 、☉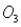 的半径相等.如果使☉ 的半径相等.如果使☉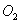 、☉ 、☉ 充分大,记BC的长度为a,请你计算出☉ 充分大,记BC的长度为a,请你计算出☉ 的半径,并给出这个圆的作法. 的半径,并给出这个圆的作法.
二、买房贷款(满分20分)
根据中国人民银行颁布的《个人住房贷款管理办法》(第十一条)“借款人应和贷款银行制定还本付息计划,贷款期限在一年以上的,按月归还贷款本息”的规定,为方便贷款银行操作和选择,中国人民银行具体规定了个人住房贷款的两种按月还本付息的办法,允许借款人和贷款银行在双方商议的基础上做出选择.
第一种办法是等额本息还款法,其还款方式已经在1999年第三届北京高中数学知识应用竞赛初赛试题的第3题中作了介绍,并要求给出月均还款额、还款总额和利息负担总和的计算公式.按照这些公式不难算出,一个人如果从银行得到买房贷款40万元,计划20年还清贷款,按规定贷款的年利率应为5.58%(折合月利率4.65%。),这时贷款人的月均还款额应为0.27696万元,还款总额为66.4717万元,利息负担总和为26.4717万元.
第二种办法是等额本金还款法(又叫等本不等息还款法),指在贷款期间内,每月除了要还清当月贷款的利息外,还要以相等的额度偿还贷款的本金.这样一来,每月偿还的贷款的利息将随本金的减少而逐月递减.因此称之为等本不等息还款法.如果这个贷款人选择了等额本金还款法在20年内偿还他所借的40万元贷款,他只需要偿还本息总合62.413万元,其中利息负担的总合为22.413万元,比前一种还款方法少支付利息4.0587万元,节省了15.33%的利息.
请你给出等额本金还款法的每月还款额、还款总额和利息负担总和的计算公式,使用这些公式计算贷款初期的前三个月的每月还款额,并进一步分析贷款人还款多少个月之后他每个月的还款负担将低于等额本息还款法的还款负担.
三、环保规划(满分15分)
某工厂的一个车间生产某种产品,其成本为每公斤27元,售价为每公斤50元.在生产产品的同时,每公斤产品产生出0.3立方米的污水.污水有两种排放方式:其一是输送到污水处理厂,经处理(假设污水处理率为85%)后排人河流;其二是直接排人河流。若污水处理厂每小时最大处理能力是0.9立方米污水,处理成本是每立方米污水5元;环保部门对排人河流的污水收费标准是每立方米污水17.6元,根据环保要求该车间每小时最多允许排人河流中的污水是0.225立方米.试问:该车间应选择怎样的生产与排污方案,使其净收益最大.
四、估算人口(满分15分)
请你搜集有关的数据,估算一下我国2000年18岁的人口数.
五、隼的分类(满分15分)
燕隼(sun)和红隼是同属于隼形目隼科的鸟类.它们的体形大小如鸽,形略似燕,身体的形态特征比较相似.红隼的体形比燕隼略大.通过抽样测量已知燕隼的平均体长约为31厘米,平均翅长约为27厘米;红隼的平均体长约为35厘米,平均翅长约为25厘米。近日在某地发现了两只形似燕隼的红隼的鸟。经测量,知道这两只鸟的体长和翅长分别为A(32.65厘米,25.2厘米),B(33.4厘米,26.9厘米)。你能否设计出一种近似的方法,利用这些数据判断这两只鸟是燕隼还是红隼?
六、女子举重(满分20分) 2000年悉尼奥运会上第一次列入女子举重的项目,各级别冠军的成绩如下: | 级别 | 运动员 | 国籍 | 体重 | 抓举 | 挺举 | 总成绩 | | 48kg 53kg 58kg 63kg 69kg 75kg >75kg | 德拉诺娃 杨 霞 门丁维尔 陈晓敏 李伟宁 乌鲁蒂亚 丁美媛 | 保加利亚 中 国 墨西哥 中 国 中 国 哥伦比亚 中 国 | 47.48kg 52.46kg 56.92kg 62.82kg 66.74kg 73.28kg 103.56kg | 82.5kg 100kg 95kg 112.5kg 110kg 110kg 135kg | 102.5kg 125kg 127.5kg 130kg 132kg 135kg 165kg | 185kg 225kg 222.5kg 242.5kg 242kg 245kg 300kg | 试利用这些数据组建模型,描述运动员举重的总成绩对运动员体重的依赖关系。根据模型分析哪些级别上运动员举重的总成绩还有较大的提高潜力。 参考答案 一、解 设☉ 、☉ 、☉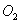 相切于点E,☉ 相切于点E,☉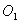 、☉ 、☉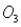 相切于点F,☉ 相切于点F,☉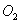 、☉ 、☉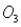 相切于点D,☉ 相切于点D,☉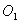 、与弧AB相切于点G。显然,点F在 、与弧AB相切于点G。显然,点F在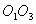 ,点G在 ,点G在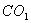 的延长线上,且 的延长线上,且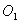 D⊥BC,易知☉ D⊥BC,易知☉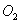 和☉ 和☉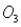 的半径为a/4。如果☉ 的半径为a/4。如果☉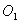 的半径为r,则有 的半径为r,则有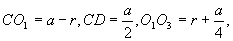 由此可得 由此可得 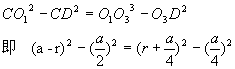
解得 r=0.3a. ☉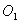 的半径为r=0.3a,它的圆心 的半径为r=0.3a,它的圆心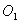 是以 是以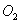 为圆心,0.55a为半径的圆与BC的中垂线的交点。 为圆心,0.55a为半径的圆与BC的中垂线的交点。 二、解 设贷款(本金)为N,贷款期限为n(月),月利率为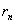 ,则根据题意,每月偿还的本金额应为 ,则根据题意,每月偿还的本金额应为 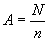
如果规定从贷款的第二个月开始于每个月的月初偿还上个月所余的本金的利息及部分本金,则第k月的月底贷款人尚欠银行的贷款额: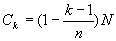 (k=1,2,...n.第k+1月的月初所偿还的第k个月的欠款的利息为: (k=1,2,...n.第k+1月的月初所偿还的第k个月的欠款的利息为: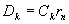 ,k=1,2,...n. ,k=1,2,...n. 第k+1月的月初的还款总额为: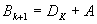 ,k=1,2,...n. ,k=1,2,...n. 整个贷款期间利息的负担总额为: 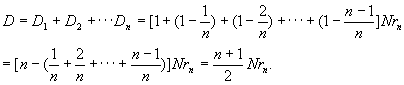
还款总额为:B=D+N。 对于上述实例我们有 N=40(万元),n=240(月),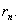 =4.654.65 =4.654.65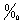 , ,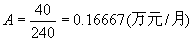 D=22.413(万元),B=62.413(万元)。 与题中给出的结果一致。 还可以得得 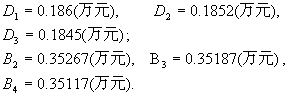
由于定额本息还款法的月均还款额为a=0.27696(万元),欲使定额本金还款法的月还款负担低于上述月均还款额,则它应满足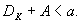 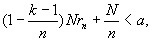
即要求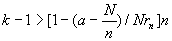 。 。 将a,N,n和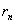 的数值代入止式,可以得到k-1>97.69由此可知,从第99个月开始,即 的数值代入止式,可以得到k-1>97.69由此可知,从第99个月开始,即
从第九年的第三个月开始定额本金还款法的每月还款负担就开始低于定额本息还款法。 三、解 设该车间净收入为每小时车间污水产生量为 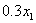 ;污水处理厂污 ;污水处理厂污
水处理量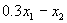 ;经污水处理厂处理后的污水排放量(l-0.85)( ;经污水处理厂处理后的污水排放量(l-0.85)(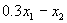 );车间产品成本 );车间产品成本 ;车间生产收入 ;车间生产收入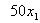 ;车间应交纳排污费用 17. 6[(1- 0.85)( ;车间应交纳排污费用 17. 6[(1- 0.85)(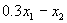 )+ )+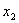 ];车间交纳的污水处理费为5( ];车间交纳的污水处理费为5(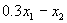 ).这样车间每小时净收人为: ).这样车间每小时净收人为: 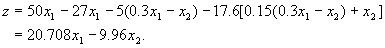 由于污水处理厂的最大处理能力,有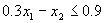 ;根据允许排入河流的最大污水量的限制,有 ;根据允许排入河流的最大污水量的限制,有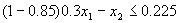 ;输送给污水处理厂的污水量应满足 ;输送给污水处理厂的污水量应满足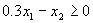 . .
综上所述,这个环保问题可归纳为以下数学模型: 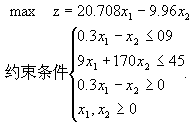
下面用图解法来角这个线性规划问题: (1)画出可行域(图中四边形OABC); (2)求最优解;从图中可以看出直线
 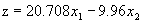 在两条直线 在两条直线
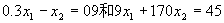 的交点上达到极大值。求出交点坐标(3.3,0.09);即当 的交点上达到极大值。求出交点坐标(3.3,0.09);即当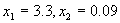 时,z取得最大值,最大值为67.44. 时,z取得最大值,最大值为67.44.
四、解 要估算2000年18岁的人口数.由于2000年的统计资料我们还不能按集到,我们根据以往的统计数据进行推算.即根据2Q00年以前,如 1999年、1998年、…、1990年、…、等年份的数据进行推算.
这里给出两种估算方法.一种是用年总人口数除以平均寿命,再根据人口分布情况进行调节,从而推算出18岁的人口数.
另一种我们以1998年的人口统计数据为依据,即根据1998年16岁的人口数来估算2000年18岁的人口数. 1998年中国人口统计年鉴中全国分年龄、性别的人口数表显示:1998年全国16岁人口总数为22010千人.全国分年龄、性别的死亡人口状况表显示:1998年16岁到17岁、17岁到18岁人口的死亡率分别为1.21%。,1.16%。
假设每年的死亡率是个常数,则我们可以做如下的估算.
1999年17岁的人口数等于1998年16岁的人口数减去这些人成长到17岁的过程中死亡的人数.这些死亡人数由1998年16岁的人口数乘以17岁的死亡率得到.
即22010-22010×I.21%=21983(千人).
2000年18岁的人口数等于1999年17岁的人口数减去这些人成长到18岁的过程中死亡的人数。这些死亡人数由1999年17岁的人口数乘以18岁的死亡率得到.
即 21983-21983×1.16%o=21957(千人).
2000年18岁的人口数为21957千人.
注:从不同的资料中收集到的数据差异可能很大.只要说清楚资料的来源,并且数据处理方式合理,就可以认为答案正确,得满分.如果自己假设一些数据作为资料来源,最多给5分;若仅是数据处理方式不当,可以给7分.
五、解法一 把(31,27),(35,25),(32.65,25.2),(31.4,26.9)看作平面直角坐标系中的点.
可以通过这两只鸟体长和翅长所确定的点与燕隼和红隼的平均体长和平均翅长所确定的点之间的距离的大小来判断他们应归属于那一类.设燕隼的平均体长为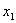 ,平均翅长为 ,平均翅长为 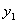 .红隼的平均体长为 .红隼的平均体长为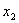 ,平均超长为 ,平均超长为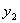 .待判鸟的体长x,翅长为y,则它与燕隼和红隼的距离分别为 .待判鸟的体长x,翅长为y,则它与燕隼和红隼的距离分别为 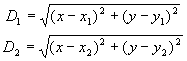
由此可得判别规则:若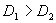 则判此鸟为红隼, 则判此鸟为红隼,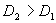 则判此鸟为燕隼, 则判此鸟为燕隼,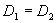 则表明仅用这些数据无法给出明确的判断。 则表明仅用这些数据无法给出明确的判断。 在问题中有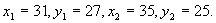 还有 还有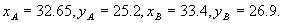 由上面的模型可以得到如下的分析结果: 由上面的模型可以得到如下的分析结果:
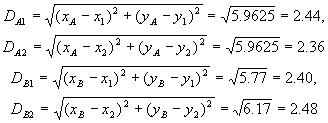 由于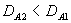 可知鸟A是红隼, 可知鸟A是红隼,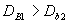 可知鸟B是红隼。 可知鸟B是红隼。 (由于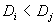 等价于 等价于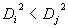 ,计算中可以不用开方)。 ,计算中可以不用开方)。 解法二 用体长与翅长的比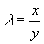 (体翅比)来进行判别。 (体翅比)来进行判别。 不难算出,对于燕隼来说有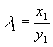 ,对于红隼 ,对于红隼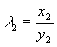 ,而对于鸟A和鸟B分别有 ,而对于鸟A和鸟B分别有 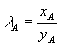 ,和 ,和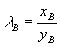 。于是可以算出 。于是可以算出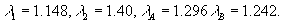
由于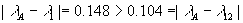 ,故鸟A为红隼。 ,故鸟A为红隼。 由于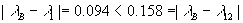 ,故鸟B为燕隼。 ,故鸟B为燕隼。 六、解 假设运动员举重的总成绩y与她们的体重x呈线性依赖关系y=a+bx。因此数据表中关于体重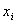 和总成绩 和总成绩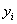 的七组数据将有关系 的七组数据将有关系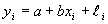 ,i=1,2,...7,其中 ,i=1,2,...7,其中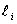 表示观测数据与模型的误差。使用最小二乘法给出直线的参数a和b的估计值,也就是求参数a和b,使得观测值和模型之间误差的平方和达到最小。经计算可以得到a=120.91,b=1.76。由此得到运动员体重和举重总成绩的模型为 表示观测数据与模型的误差。使用最小二乘法给出直线的参数a和b的估计值,也就是求参数a和b,使得观测值和模型之间误差的平方和达到最小。经计算可以得到a=120.91,b=1.76。由此得到运动员体重和举重总成绩的模型为 y=120.91+1.76x (1) 将七个运动员的体重代入模型(1),可以得到她们举重成绩的模型值。与她们的实际举重总成绩比较如下: | 级别 | 48kg | 53kg | 58kg | 63kg | 69kg | 75kg | >75kg | | 体重 | 47.48kg | 52.46kg | 56.92kg | 66.74kg | 73.28kg | 73.28kg | 103.56kg | | 实际
成绩 | 185.00kg | 225.00kg | 222.50kg | 242.00kg | 245.00kg | 245.00kg | 300.00kg | | 模型(1)成绩 | 204.50kg | 213.30kg | 221.10kg | 238.40kg | 249.90kg | 249.90kg | 303.20kg | 从拟合效果上看有四个级别较好,一个级别较差;48公斤级别的运动员没能取得理想的成绩,使用这个数据参与建模将会增加误差,降低模型的可信程度。去掉这组数据,使用其余的六组数据来估计模型的参数a和b。类似的计算可得a=141.8,b=1.51,于是得到修正的模型为 y=141.8+1.51x (2) 将七个运动员的体重代入模型(2),可以得到她们举重成绩的模型值。与她们的实际举重成绩及模型(1)成绩比较如下: | 级别 | 48kg | 53kg | 58kg | 63kg | 69kg | 75kg | >75kg | | 体重 | 47.48kg | 52.46kg | 56.92kg | 62.82kg | 66.74kg | 73.28kg | 103.56kg | | 实际
成绩 | 185.00kg | 225.00kg | 222.50kg | 242.50kg | 242.00kg | 245.00kg | 300.00kg | | 模型(1)成绩 | 204.50kg | 213.30kg | 221.10kg | 231.50kg | 238.40kg | 249.90kg | 303.20kg | | 模型(2)成绩 | 213.30kg | 220.80kg | 227.50kg | 236.40kg | 242.30kg | 252.20kg | 297.80kg | 从拟合效果上看,除去48公斤级以外的六个级别,模型(2)的总体拟合效果要优于模型(1)。因此可以用模型(2)来描述女子举重总成绩与运动员体重之间的关系。比较实际成绩与模型(2)的成绩,可以看出,48公斤、58公斤和75公斤级的实际成绩均低于模型的成绩,差数分别为28.3kg,5kg,7.2kg.因此可以认为,在这次比赛中上述几个级别的成绩还有提高潜力。 注1 这个问题也可以组建幂函数的模型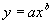 来拟合上面的数据,结论是: 来拟合上面的数据,结论是: 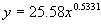 和 和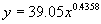 (六组数据拟合的效果与线性模型差异不大,最后结论也相同。) (六组数据拟合的效果与线性模型差异不大,最后结论也相同。)
注2 48公斤的数据参与建模是不恰当的,因为它有较大的偏差,不能反映实际的规律。虽然利用七组数据所得的模型(1)也可以得到最后的结论,但模型的信度是较低的。如果此题仅用模型(1)而缺乏讨论,在评分时要适当减掉一些分数。 |