高考能力测试步步高数学基础训练30
基础训练30 轨迹与最值问题
●训练指要
掌握直译法、相关点法、参数法求轨迹方程，对所求的轨迹应注意其完备性与纯粹性；掌握代数法与几何法求解析几何最值.
一、选择题
1.点P为双曲线
＝1上异于顶点的任意一点，F1、F2是双曲线两焦点，则△PF1F2重心轨迹方程是
A.9x2－16y2＝16(y≠0) B.9x2＋16y2＝16(y≠0)
C.9x2－16y2＝1(y≠0) D.9x2＋16y2＝1(y≠0)
2.点P与两定点F1(－a，0)、F2(a，0)(a＞0)的连线的斜率乘积为常数k，当点P的轨迹是离心率为2的双曲线时，k的值为
A.3 B.
C.± D.４
3.若实数x,y满足x2＋y2－2x＋４y＝0，则x-2y的最大值为
A.5 B.10 C.9 D.5+2
二、填空题
4.抛物线y2=4x的经过焦点的弦的中点轨迹方程是_________.
5.圆x2+y2-4x+6y-12=0过点(-1，0)的最长弦长为L，最短弦长为l，则L-l=_________.
三、解答题
6.求过点M(1，-1)，离心率为
,且以y轴为准线的椭圆的右焦点F的轨迹方程.
7.设椭圆与双曲线有共同的焦点F1(-4，0)，F2(4，0)，并且椭圆的长轴长是双曲线实轴长的2倍，求椭圆与双曲线交点的轨迹.
8.过椭圆2x2+y2=2的左焦点的直线交椭圆于A、B两点，求△AOB面积的最大值(O为坐标原点).
高考能力测试步步高数学基础训练30答案
一、1.A 2.A
3.B
提示：已知条件化为(x－1)2+(y+2)2=5,令x=1+·cosα,y=－2+sinα化为三角函数求最值，或令x－2y=t,数形结合求最值.
二、4.y2=2(x－1) 5.10－2
三、6.
+2(y+1)2=1
提示：设F(x,y),则左焦点F′(x－2c,y),
∵
,∴a2=2c2,又y轴为左准线，故x=
+c=3c,
∴c=
,即F′(
),又M在椭圆上，
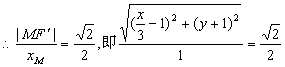
F的轨迹方程为
7.所求轨迹为圆心在(5，0)，半径为3的圆，除去(2，0)和(8，0)两点；或圆心在(－5，0)，半径为3的圆，除去(－2，0)和(－8，0)两点.
8.