高三数学试题4
一、选择题 （共60分，把正确答案的序号填在答题表中。）
1.已知集合
和
，那么
的充要条件是
（A）
（B）
（C）
（D）
2.若
和
分别是方程
的两个实根，则实数
、
的关系是
（A）
（B）
（C）
（D）
3.已知
、
是一元二次方程
的两个实根，
、
分别是 、的等差中项和等比中项，则有
（A）
（B）
（C）
（D）和的大小关系不能确定
4.“
”成立是“
”成立的
（A）充要条件 （B）既不充分又不必要条件
（C）充分非必要条件 （D）必要非充分条件
5. 将函数y=sin2x的图象按向量a=(-
,1)平移后所得图象的解析式是
（A）y=sin(2x-)+1（B）y=sin(2x+)+1（C）y=sin(2x+
)+1（D）y=sin(2x-)+1
6.已知c,d是两非零向量，若d=(b·c)a-(a·c)b 则向量c与d
（A）一定平行 (B)一定垂直 (C)一定成锐角 (D)一定成钝角
7.已知
、
为正实数，且、
、
、成等差数列，、
、
、成等比数列，则
的取值范围是
（A）
（B）
（C）[4，
（D）（
8.若点P(a,b)与点Q(b-1,a+1)关于直线L对称，则直线L的方程为
（A）x+y=0 (B) x-y=0 (C) x+y+1=0 (D) x-y+1=0
9、已知圆(x-3)2+(y+4)2=4和直线y=kx相交于点P、Q两点,则两向量
与
的数量
积为
（A）
（B）1+k2 （C）4 （D）21
10经过点（1/2，2）且与双曲线4x2-y2=1仅有一个公共点的直线有
（A）一条 （B）两条 （C）三条 （D）四条
11直线mx+y+2=0与线段MN有交点，其中M(－2，１)，N(3, 2)，则实数m
的取值范围是 ( )
（A）
≤m≤
（B）m≤或m≥
（C）
≤m≤
（D）m≤或m≥
12.设函数
，
，若当
时,
恒成立，则
的取值范围是
（A）
（B）
（C）
（D）
二、 填空题（共20分，把答案填写在题中横线上）
13.双曲线9x2-16y2=144上的一点P到右焦点距离为5，则点P到左准线
距离为 ．
14.已知
，则
．
15.已知向量a=(cosX,sinX),向量a+b=(3,4),则b的最大值为_________
16过点A（0，1）和B（4，m）并且与x轴相切的圆只有一个，则实数m=_______
三、解答题（共70分，解答题应写出文字说明，证明过程或演算步骤．）
17.（满分10分） 已知向量a,b满足a=
,b=3,向量a与b的夹角为450,求使向量a+mb 与向量ma+b的夹角是锐角时，m的取值范围。
18（满分10分）在三角形ABC中，已知tanA=
，tanB=
，且最长边为1，求角C的大小和三角形ABC中最短边的长。
19（满分12分）函数f(x)在区间[a,b]上有定义，且令f(a)=f(b)，如果对于任意不同的 x1,x2∈[a,b]，均有f(x1)-f(x2)<kx1-x2,求证，2f(x1)-f(x2)<k(b-a)
20（满分12分）设声速是
米／秒，在地点
处听到地点
处发出的声音的强度与、的距离的平方成反比例．在相距
米的、
两个哨所听到同一发炮弹爆炸声的时间相差６秒，且处声音强度是处声音强度的４倍，试确定炮弹爆炸点到
的中点
的距离
及
的正切值。
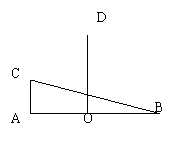21（满分12分）如图，在直角三角形ABC中，∠CAB=900，AB=2，AC=
，DO⊥AB于O，OA=OB，DO=2，曲线E过C点，动点P在E上运动，且保持PA+PB的值不变，（1）建立适当的坐标系,求曲线E的方程 （2）过D点的直线l与曲线E相交于不同的两点M、N,且M在D、N之间,设DM与DN的比值为m,求m的取值范围.
22（满分14分）已知点列Pn(an，bn)都在直线l：y=2x+1上，P1为直线l与y轴的交点，数列{an}成等差数列，公差为1，
（1）求数列{an}，{bn}的通项公式；
（2）求证
（3）若f(n)=
，问：是否存在k∈N，使f(k+5)=2f(k)成立，若存在，求出k的值，若不存在，说明理由。
参考答案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | B | B | C | C | B | C | D | D | D | B | B |
二、填空题
13．52/5
14．
15．6
16．0，1，
三、解答题
17．
且m≠1
18．C=1350 ， b=
19．证：10 若x1-x2≤
时，则f(x1)-f(x2)<kx1-x2≤
∴2f(x1)-f(x2)<k(b-a)
20
不妨设x2>x1，若x1-x2=x2-x1>时
f(x1)-f(x2)= f(x1)-f(a)+f(b)-f(x2)
≤f(x1)-f(a)+f(b)-f(x2)
<k(-a+x1)+k(b-x2)
=k(x1-x2)+k(b-a)
<
(b-a) ∴2f(x1)-f(x2)<k(b-a)
20．OM=
a， tan∠MOB=
MA=2MB
MA-MB=6a ∴MB=6a, MA=12a
(12a)2=(6a)2+(10a)2-2×6a×10a×cosθ ∴cosθ=
∴OM2=(5a)2+(6a)2-2×5a×6a×cosθ=65a2
∴OM=a
(6a)2=65a2+25a2-2×5a×a·cos∠MOB
∴cos∠MOB=
sin∠MOB=
∴tan∠MOB=
21．①
=1 ②m∈[
，1）
（1）∵CA+CB=
∴a= ， C=1 ∴b=1
∴曲线E的方程为：=1
（2）设直线：y=kx+2
由 y=kx+2 得 x2+2（kx+2）2=2
=1
∴（1+2k2）x2+8kx+6=0
解法：利用图形分析：
是单调函数
当直线与椭圆相切时，取最大值1 当直线为y轴时，取最小值
∴m∈[，1）
22．（1）a1=0， b1=1 ∴an=n-1， bn=2n-1
（2）P1Pn2=（
）2=
=5（n-1）2
左=
＜
=
=
（3）若k为奇数 f（k+5）=2f（k）=2（k-1）
f（k+5）=2（k+5）-1
∴2k+9=2k-2 不可能
若k为偶数 f（k+5）=k+5-1+k+4
2f（k）=2（2k-1）=4k-2
∴k+4=4k-2 ∴k=2