高三数学同步测试—分类讨论思想
一、选择题(本题每题5分,共60分)
1.不等式![]() 的解集为 ( )
的解集为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.函数![]() 的图象的基本形状是 ( )
的图象的基本形状是 ( )
|
|
3.在下列条件中,可判断平面α与β平行的是 ( )
A.α、β都垂直于平面r.
B.α内存在不共线的三点到β的距离相等.
C.l,m是α内两条直线,且l∥β,m∥β.
D.l,m是两条异面直线,且l∥α,m∥α, l∥β,m∥β.
4.若![]() ,则正常数a、b的大小关系是
( )
,则正常数a、b的大小关系是
( )
A.a>b B.a<b C.a=b D.不能确定
5.设函数![]() ,则
,则![]() 的值等于 ( )
的值等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.如果不等式![]() 成立的充分非必要条件是
成立的充分非必要条件是![]() ,则实数m的取值范围是
,则实数m的取值范围是
( )
A.![]() B.
B.![]()
C.![]() 或
或![]() D.
D.![]() 或
或![]()
7.设![]() ,关于x的方程
,关于x的方程![]() ,以下结论正确是
,以下结论正确是
( )
A.仅当a > 1时,方程有唯一解 B.方程必有唯一解
C.仅当0< a < 1时,方程有唯一解 D.方程无解
8.过点(0,1)并与抛物线y2=mx(m>0)只有一个公共点的直线有 ( )
A.由m值而定 B.1条 C.2条 D.3条
9.已知![]() ,
,![]() 是抛物线
是抛物线![]() 上不同两点,则
上不同两点,则![]() ·
·![]()
![]() 是直线
是直线![]() 通过抛物线焦点是
( )
通过抛物线焦点是
( )
A.充分不必要条件 B.充分必要条件
C.必要不充分条件 D.既非充分也非必要条件
10.已知![]() 且
且![]() ,函数
,函数![]() 的图象与函数
的图象与函数![]() 的图象的交点的个数是
的图象的交点的个数是
( )
A.1个 B.2个 C.3个 D.4个
11.在直角坐标系xOy中,已知△AOB三边所在直线的方程分别为![]() ,则△AOB内部和边上整点(即横、纵坐标均为整数的点)的总数是 ( )
,则△AOB内部和边上整点(即横、纵坐标均为整数的点)的总数是 ( )
A.95 B.91 C.88 D.75
二、填空题(本题每小题4分,共16分)
13.已知数列a+b,a2+2b,a3+3b,······,a n+nb,··· 的前n项和为Sn,则S10= .
14.若关于x的方程![]() 与
与![]() 的四个实根适当排列后可构成一个首项为1的等比数列,则
的四个实根适当排列后可构成一个首项为1的等比数列,则![]() 的值为 .
的值为 .
15.一同学在电脑中打出如下若干个圆(图中●表示实圆,○表示空心圆):
●○●●○●●●○●●●●○●●●●●○●●●●●●○
若将此若干个圆依次复制得到一系列圆,那么在前2002个圆中,有 个空心圆.
16.若对![]() 个向量
个向量![]() 存在
存在![]() 个不全为零的实数
个不全为零的实数![]() ,使得
,使得![]() 成立,则称向量
成立,则称向量![]() 为“线性相关”.依此规定,
能说明
为“线性相关”.依此规定,
能说明![]() ,
,![]() ,
,![]() “线性相关”的实数
“线性相关”的实数![]() 依次可以
依次可以
取 (写出一组数值即可,不必考虑所有情况).
三、解答题(本题17—21小题每题12分,22小题14分,共74分)
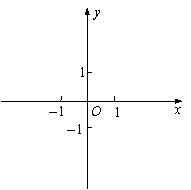 19.已知函数
19.已知函数![]() (x>0),g (x)是定义
(x>0),g (x)是定义
在R上奇函数,且满足:当x>0时,g (x)=f (x).
求g (x)的表达式并画出图象.
20.已知![]() ≤a≤1,若函数f(x)=ax2-2x+1在区间[1,3]上的最大值为MA.,令gA.= MA.-NA..(I)求gA.的函数表达式;
≤a≤1,若函数f(x)=ax2-2x+1在区间[1,3]上的最大值为MA.,令gA.= MA.-NA..(I)求gA.的函数表达式;
(II)判断函数gA.在区间[![]() ,1]上的单调性,并求出gA.的最小值 .
,1]上的单调性,并求出gA.的最小值 .
21.某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品x(百台),其总成本为G(x)万元,其中固定成本2万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本);销售收入R(x)(万元)满足:
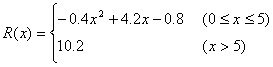 假定该产品产销平衡,那么根据上述统计规律.(1)要使工厂有赢利,产量x应控制在什么范围?(II)工厂生产多少台产品时,可使赢利最多?(III)求赢利最多时每台产品的售价.
假定该产品产销平衡,那么根据上述统计规律.(1)要使工厂有赢利,产量x应控制在什么范围?(II)工厂生产多少台产品时,可使赢利最多?(III)求赢利最多时每台产品的售价.
22.如图,已知圆A、圆B的方程分别是![]() 动圆P与圆A、圆B均外切,直线l的方程为:
动圆P与圆A、圆B均外切,直线l的方程为:![]() .
.
(I)求圆P的轨迹方程,并证明:当![]() 时,点P到点B的距离与到定直线l距离的比为定值;
时,点P到点B的距离与到定直线l距离的比为定值;![]()
(II) 延长PB与点P的轨迹交于另一点Q,求![]() 的最小值;
的最小值;
(III)如果存在某一位置,使得PQ的中点R在l上的射影C,满足![]() 求a的取值范围.
求a的取值范围.

数学参考答案及评分标准(十四)
一、1.C 2. A 3.D 4.B 5.D 6.A 7. B 8. D 9.B 10.C 11.B 12.A.
二、13. 当![]() 时,
时, ![]() ; 当
; 当![]() 时,
时, ![]() 14. 1 15 .61
14. 1 15 .61
16. 只要写出![]() 中一组即可,如
中一组即可,如![]() 等.
等.
三、17. ①设![]() (k为非负整数),
原式
(k为非负整数),
原式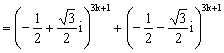
![]()
同理可得,②当![]() (k为非负整数)时,原式
(k为非负整数)时,原式![]() 所以,原式
所以,原式![]()
18. 原不等式等价于 ![]() ①或
①或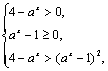 ②
②
由①得![]() 由②得
由②得![]()
当a>1时,![]() 当a=1时,x∈R.
当a=1时,x∈R.
(19) ∵g (x)是R上奇函数,∴g (0)=0.
|
|
 当x<0时,-x>0
当x<0时,-x>0
g (x)=-g (-x)=-f (-x)=-2x .
∴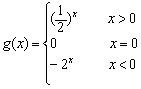 .
.
(20) (I)∵![]() 的图象为开口向上的抛物线,且对称
的图象为开口向上的抛物线,且对称
轴为![]() ∴f(x)有最小值
∴f(x)有最小值 ![]() . 当2≤
. 当2≤![]() ≤3时,a∈[
≤3时,a∈[![]() 有最大值
有最大值
MA.=f(1)=a-1;当1≤![]() <2时,a∈(
<2时,a∈(![]() 有最大值MA.=f(3)=9a-5;
有最大值MA.=f(3)=9a-5;
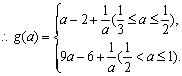
(II)设![]()
![]() 上是减函数.
上是减函数.
设![]() 上是增函数.
∴当
上是增函数.
∴当![]() 时,gA.有最小值
时,gA.有最小值![]() .
.
21.依题意,G(x)=x+1.设利润函数为f(x),则 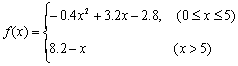 .
.
(Ⅰ)要使工厂有赢利,即解不等式f(x)>0,当![]() 时,解不等式
时,解不等式 ![]() 即
即![]()
当x>5时,解不等式![]()
综上,要使工厂赢利,x应满足![]() ,即产品应控制在大于100台,小于820台的范围内.
,即产品应控制在大于100台,小于820台的范围内.
(II)![]() ,故当x=4时,f(x)最大值3.6.
,故当x=4时,f(x)最大值3.6.
而当x>5时, f(x)<8.2-5=3.2.所以,当工厂生产400台产品时,赢利最多.
(III)即求x=4时的每台产品的售价.此时售价为![]() (万元/百台)=240元/台.
(万元/百台)=240元/台.
22.(I)设动圆P的半径为r,则|PA|=r+![]() ,|PB = r +
,|PB = r + ![]() ,
,
∴ PA -|PB = 2.
∴ 点P的轨迹是以A、B为焦点,焦距为4,实轴长为2的双曲线的右准线的右支,其方程为 ![]() (x ≥1).若
(x ≥1).若![]() , 则l的方程
, 则l的方程![]() 为双曲线的右准线, ∴点P到点B的距离与到l的距离之比为双曲线的离心率e = 2.
为双曲线的右准线, ∴点P到点B的距离与到l的距离之比为双曲线的离心率e = 2.
(II)若PQ的斜率存在,设斜率为k,则直线PQ的方程为y = k ( x-2 )代入双曲线方程得:
![]()
![]()
由 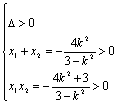 , 解得
, 解得![]() >3.
>3.
∴ |PQ|=![]() .
.
当直线的斜率存在时,![]() ,得
,得![]() ,|PQ=6.∴ |PQ的最小值为6.
,|PQ=6.∴ |PQ的最小值为6.
(III) 当PQ⊥QC时,P、C、Q构成Rt△. ∴ R到直线l的距离|RC=![]() .
.
∴ ![]() ≥6,
≥6,![]() ≥3. 又
≥3. 又 ![]() ,
,
∴ ![]() -a≥3. ∴ a≤
-a≥3. ∴ a≤![]() .
.
∵ ![]() >3, ∴
>3, ∴ ![]() 的范围是(-1,+∞),故有a≤-1.
的范围是(-1,+∞),故有a≤-1.