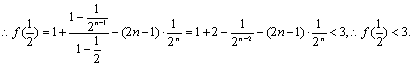高中学生学科素质训练
高三数学综合测试题—(4)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。共150分,考试时间120分钟。
第Ⅰ卷(选择题,共60分)
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.设10件产品中有4件不合格,从中任取两件,已知所取的2件产品中有1件是不合格品,则另一件也是不合格品的概率是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.设函数![]() ( )
( )
A.2 B.![]()
C.![]() D.
D.![]()
3.已知直线![]() 平行,则实数a的值是( )
平行,则实数a的值是( )
A.-1或2 B.0或1 C.-1 D.2
|
A. B. C. D.
5.(x—1)11的展开式中x的系数最小的项是 ( )
A.第5项 B.第6项 C.第7项 D.第8项
6.正方体ABCD—A1B1C1D1中,E、F分别是AA1与CC1的中点,则直线ED与D1F所成角的大小是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.已知下列命题:
![]() ①若直线
①若直线![]() ∥平面
∥平面![]() ,直线
,直线![]() ,则a∥b;
,则a∥b;
![]() ②若直线a∥平面
②若直线a∥平面![]() ,
, ![]() 平面
平面![]() 内的射影为
内的射影为![]() ∥b;
∥b;
③若直线a⊥直线c,直线b⊥直线c,则直线a∥直线b
④若α、β、![]() 、δ是不同的平面,且满足
、δ是不同的平面,且满足![]()
其中正确命题的个数有 ( )
A.0个 B.1个 C.2个 D.3个
8.若复数z1=2-a+ai与复数z2=b-1+(1-b)i(a,b∈R)满足z1=z2且![]() ,则a,b的值分别是 ( )
,则a,b的值分别是 ( )
A.1,2 B.2,1 C.1,0 D.0,1
![]() 9.集合
9.集合![]() 当A
当A![]() B时,则 ( )
B时,则 ( )
A.a>3 B.1≤a<3
C.a>9或a<3 D.3<a<9
10.直线l:y=kx+1与双曲线C:x2—y2=1的左支仅有一个公共点, 则k的取值范围是 ( )
A.k=1 B.-1<k≤1
C.-1<k≤1或k=![]() D.-1<k≤1或
D.-1<k≤1或![]() ≤k<2
≤k<2
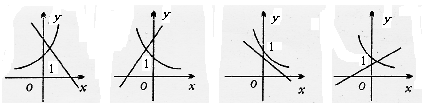
11.函数![]() 是 ( )
是 ( )
A.偶函数 B.既是奇函数又是偶函数
C.奇函数 D.既不是奇函数也不是偶函数
12.在一张节目表中有6个节目,如果保持这些节目的相对顺序不变,再添加进去3个节目,则不同的添加方法有 ( )
A.210种 B.252种 C.504种 D.505种
第Ⅱ卷(非选择题,共90分)
二、填空题(本大题共4小题,共16分,把答案填在题中横线上)
13.方程log2(9—2x)=3—x的解集是 .
14.点M在抛物线y2=ax上运动,点N与点M关于点A(1,1)对称,则点N的轨迹方程是 .
15.已知等比数列{an}的前3项分别是![]() ,其中a∈R,则
,其中a∈R,则![]() (a1+a2+…+an)=
.
(a1+a2+…+an)=
.
16.将直角三角形ABC沿斜边上的高AD折成120°的二面角,已知直角边![]() ,那么二面角A—BC—D的正切值为
.
,那么二面角A—BC—D的正切值为
.
三、解答题(本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)
设随机变量![]() 的概率密度函数为
的概率密度函数为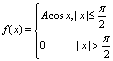 ,(1)求系数A;(2)求F(x)=P(ξ<x)的表达式并作出它的图象.
,(1)求系数A;(2)求F(x)=P(ξ<x)的表达式并作出它的图象.
18.(本小题满分12分)
设![]()
(Ⅰ)求z的三角形式;
(Ⅱ)当0≤a≤3时,求![]() 的取值范围;
的取值范围;
(Ⅲ)当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
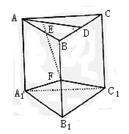
19.如图,(本题满分12分)
已知:直三棱柱ABC—A1B1C1中,AB=AC,D为BC中点,F为BB1上一点,且BF=BC=2,FB1=1.
(Ⅰ)求证:AD⊥平面BB1C1C;
(Ⅱ)若E为AD上不同于A、D的任一点,求证:EF⊥FC1;
(Ⅲ)若A1B1=3,求FC1与平面AA1B1B所成角的大小;
(Ⅳ)在(Ⅲ)的条件下,求点C1在A1B1上的射影到平面A1FC1的距离.
|
20.(本题满分12分)
带有若干枚炸弹的轰炸机向敌方某铁路干线的枢纽部位投弹,若炸弹落到铁路两旁40米以内,铁路交通被破坏,若飞机在准确投弹的情况下,落弹点与铁路的距离ξ的概率密度函数为: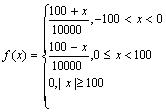 ,为了使敌方的铁路交通受到破坏的概率不低于0.95,轰炸机至少应投下多少颗炸弹?
,为了使敌方的铁路交通受到破坏的概率不低于0.95,轰炸机至少应投下多少颗炸弹?
21.(本题满分12分)
已知椭圆中心在坐标原点O,一条准线的方程x=1,过随圆的左焦点F,且斜率为1的直线l交椭圆于A,B两点
(Ⅰ)设M为线段AB的中点,直线AB与OM的夹角为![]() =2时,求椭圆的方程;
=2时,求椭圆的方程;
(Ⅱ)当A,B两点分别位于第一、三象限时,求椭圆短轴长的取值范围.
22.(本题满分14分)
已知![]() 组成等差数列(n为正偶数),又
组成等差数列(n为正偶数),又![]()
(Ⅰ)求数列的公差d;
(Ⅱ)试比较![]() 与3的大小,并说明理由.
与3的大小,并说明理由.
高三数学综合测试题参考答案
(四)
一、选择题1.A 2.B 3.C 4.D 5.B 6.A 7.B 8.A 9.A 10.C 11.D 12.C
二、填空题13.![]() 14.
14.![]() 15.9
15.9
16.![]() .
.
三、解答题
17.(1)![]()
①当![]() ②当
②当![]()
③![]()
18.(Ⅰ)![]()
(Ⅱ)![]()
|
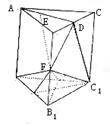
19.如右图,(Ⅰ)∵AB=AC且D为BC中点,∴AD⊥BC,又
∵ABC-A1B1C1是直三棱柱,∴平面ABC⊥平面BB1C1C,
∴AD⊥平面BB1C1C.(Ⅱ)连结DF,DC1,由已知可求得
![]()
即DF⊥FC1,由三垂线定理,∴EF⊥FC1.
(Ⅲ)作C1G⊥A1B1于G,∵平面C1A1B1⊥平面AA1B1B,∴C1G⊥平面AA1B1(B)连结FG,∴∠C1FG为所求角.在Rt△ABD中,易求得
![]()
![]()
(Ⅳ)由(Ⅲ)知G为C1在A1B1上射影,作B1H⊥A1C1于H,连结FH,
![]() 设h为G到平面A1FC1的距离.
设h为G到平面A1FC1的距离.
![]()
![]()
![]()
20.一颗炸弹落在铁路两旁40米以内的概率为:![]() ∴一颗炸弹落到40米以外的概率为
∴一颗炸弹落到40米以外的概率为![]() 设投n颗炸弹能使破坏概率不低于0.99,
∴
设投n颗炸弹能使破坏概率不低于0.99,
∴![]()
即0.36n≤0.01,∵0.364=0.016,0.365=0.00601,∴n≥5.
21.(Ⅰ)设椭圆方程为![]()
![]()
![]()
![]() 又AB与OM夹角α满足
又AB与OM夹角α满足![]() *∵中心在原点,一条准线为x=1,
*∵中心在原点,一条准线为x=1,![]()
(Ⅱ)∵直线l过左焦点F(—c,0),∴l在y轴上截距为c,当A,B分别在第一、三象限时,c<b,∴c2<b2.
又b2=a2=c2,由(Ⅰ)知a2=c,![]() 可见b2最大为
可见b2最大为![]() (当
(当![]() 时)
时)
![]() ∴椭圆短轴长的范围是(0,1)
∴椭圆短轴长的范围是(0,1)
22.(Ⅰ)![]()
(Ⅱ)![]()
由(Ⅰ)结论可知![]()
![]()
![]() ①
①
①式两边同乘以![]() 得:
得:![]() ②
②
①—②得:![]()
即![]()