高三数学综合测试题—（5）

高中学生学科素质训练

　

高三数学综合测试题—（5）

　　　 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。共150分。考试时间120分钟。

第Ⅰ卷（选择题，共60分）

一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．若的值的范围是　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　B．　　　　　　　 C．　　　　　　　　 D．[0，1]

2．椭圆与直线交于A、B两点，过原点与线段AB中点的直线的斜率为的值为　　　　　 　　　　　　　　　　　　　　　　（　　）

　　　 A． 　　　　　　　　 B．　　　　　　　　 C．　　　　　　　　 D．

3．当以半径R的球的一个截面为底面，球心为顶点的圆锥的体积最大时，此圆锥的侧面展开图的圆心角为　　　　　　　　　 　　（　　）

　　　 A．　　　　　　　B．　　　　　　　C．　　　　　　　　 D．

4．已知函数是以3为周期的奇函数，而且，则　　（　　）

　　　 A．　　　　　　　　B．　　　　　　　C．　　　　　　　　 D．

5．已知的辐角主值θ的取值范围是　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　　　　　　　　 B．

　　　 C．　　　　　　　　　　　　　　　　　 D．

6．若方程有解，则a的取值范围是　　　　　　　　　　　 （　　）

　　　 A．　B．　　　　　　　　C．　　　　D．

7．⊙O₁与⊙O₂的半径分别为1和2，O₁O₂=4，动圆与⊙O₁内切而与⊙O₂外切，则动圆圆心轨迹是　　　　　　　 　　　　　　　　　　　　　　　　（　　）

　　　 A．椭圆　　　　　　　　　　　　　　　　　　　　　　　　　B．抛物线　　　　　　　　

　　　 C．双曲线　　　　　　　　　　　　　　　　　　　　　　　 D．双曲线的一支

8．要使函数在区间[]上出现的次数不少于4次，不多于8次，则k的值是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．2　　　　　　　　　　　　　　　　　　　　　　　　　　　　B．3　　　　　　　　　　　　

　　　 C．45　　　　　　　　　　　　　　　　　　　　　　　　　　　D．2或3

9．如图P是矩形ABCD的边AD上的一点，CP、CA把矩形分成三个三角形.若这三个三角形绕直线AB旋转一周，所得几何体

　　　 的体积相等，则AP:AD=　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　B．

　　　 C．1:2　　　　　　　　　　　D．1:3

10．设集合映射.使对任意都有是奇数，这样的映射f的个数为　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．122　　　　　　　　　　 B．15　　　　　　　　　　　 C．50　　　　　　　　　　　D．27

11．正三棱锥P—ABC中，∠APB=∠BPC=∠CPA=90°，PA=PB=PC=a，AB的中点M，一小虫沿锥体侧面由M爬到C点，最短路段是　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　 B．　　　　　　　　　 C．　　　D．

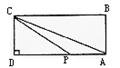
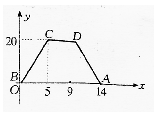
12．ABCD是四边形，动点P沿折线BCDA由B点向A点运动，P点移动的路程为x，△ABP的面积为S.函数S=的图像如图所示，给出以下四个结论：①ABCD是等腰梯形；②ABCD是平行四边形；③若Q是AD中点，那么△ABQ的面积为10；

　　　 ④当时，函数的解析

　　　 式是.其中正确命题的序号是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．①③　　　　　　　　　 B．③④　　　　　　　　　

　　　 C．①③④　　　　　　　 D．②③④

第Ⅱ卷（非选择题，共90分）

二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上.

13．设　　　　 .

14．^*，圆的周长为=

　　　　　　　 .

15．A、B两人从相距32千米的两地同时相向出发，A以匀速4千米/小时前进，B第1小时以2千米/小时速度匀速前进，第2小时以2.5千米/小时匀速前进，……，第k小时以千米/小时的速度匀速前进，……则A、B相遇历时　　　　　 .

16．数1447，1005，1231有某些共同点，即每一个都是从1开头的四位数，且每个数恰有两个数码相同，这样的数共有　　　　  个.

三、解答题：本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤.

17．（本小题满分12分）

　　　 若正数数列{}满足^*）恒在双曲线上，

　　　 （Ⅰ）求证{}是等差数列，并求的表达式.

　　　 （Ⅱ）设数列{}中，

18．（本小题满分12分）

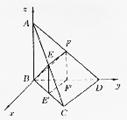
　　　 在四面体ABCD中，AB⊥平面BCD，BC=CD，∠BCD=90°，∠ADB=30°E，F分别

是AC，AD的中点.

　　　 （1）求证：平面BEF⊥平面ABC；

　　　 （2）求平面BEF和平面BCD所成的角.

19．（本小题满分12分）

　　　 已知抛物线经过定点A（0，2），而且x轴为准线.

　　　 （Ⅰ）求抛物线顶点的轨迹C方程；

　　　 （Ⅱ）问经过定点，是否存在一对互相垂直的直线同时都与轨迹C有公共点？证明您的结论.

20．（本小题满分12分）

已知函数在定义域上是减函数，问是否存在实数k，使得

对一切实数x恒成立?

21．（本小题满分12分）

南方某地市场信息中心为了分析本地区蔬菜的供求情况，通过调查得到家种野菜“芦蒿的市场需求量和供应量数据（见下表）：

表1　 芦蒿的市场需求量信息表

需求量y吨	40	38	37.1	36	32．8	30
价值x千元/吨	2	2.4	2.6	2.8	3.4	4

表2　芦蒿的市场供应量信息表

价值y千元/吨	2	2.5	3.2	4	4.6	5
供应量x吨	29	32	36.3	40.9	44.6	47

　　　 （Ⅰ）试写出描述芦蒿市场需求量y关于价格x的近似函数关系式;

　　　 （Ⅱ）试根据这些信息，探求市场对芦蒿的供求平衡量（需求量与供应量相等，就称

为供求平衡量，近似到1吨）.

22．（本小题满分14分）

　　　 已知二次函数和一次函数

　　　 （Ⅰ）求证：的图象交于两个不同的点A、B；

　　　 （Ⅱ）求证：A、B两点分别位于直线x=1的两侧.

　　　 （Ⅲ）求线段AB在x轴上的射影长的取值范围.

高三数学综合测试题参考答案

（五）

一、选择题

1．B　2．A　3．D　4．D　5．D　6．D　7．D　8．D　9．B　10．C　11．D　12．C

二、填空题

13．∴A－B=（3－1）⁷=2⁷=128.　　 14．

15．总时间为（小时） 16．共有432个.

三、解答题

17．（1）由题设知为首项，公差为4的等差数列，

　 （2）解法一 即

　　　　

　　　　　　　　.

　　　　解法二 用数学归纳法.当n=2时，

　　　　时不等式成立，即

　　　　　　　　当

　　　　　　　　　时结论成立.

　　　　　　　　由以上证明：知不等式对的自然成立.

18．（1）建立如图所示的空间直角坐标系，取A（0，0，a）.

　　　　　　　　由

　　　　　　　　

　　　　　　　　所以

　　　　　　　　因为

　　　　　　　　所以

　  （2）作

　　　　　　　　 

　　　　　　　　所以

　　　　　　　　所以θ=即平面BEF和平面BCD所成的角为

19．设抛物线顶点，则焦点由定义得AF=AD，D为原点，即，

　　 化简得，所以所求轨迹C为：顶点M不在抛

物线的准线x轴上，

（2）设l为过点B且与C有公共点的直线，其斜率为k（k显然存在）

由

而当若存在一对过定点B而互相垂直的直线矛盾，所以过点B不存在一对互相垂直的直线同时都与轨迹C有公共点.

20．假设存在实数k符合条件，则对一切实数x均成立.

① ②

　　　　即　　 对均成立.要使①对恒成立，只须的最小值，即要使②对恒成立，只段的最大值，而解不等式组

　　　 ，即存在实数符合题意.

21．（1）在直角坐标系中，由表1描出数对（x, y）对应的点，由图可知这些点近似地构成一条直线（其中有4个点恰在一直线上），所以芦蒿的市场需求量关于价格的近似函数关系式为：，即①

（2）与上同理可知芦蒿市场价格关于供应量的近似函数关系为，所以芦蒿市场供应量关于价格的近似函数关系式为②

联立①、②解方程组得，则市场对芦蒿的供求平衡量为35吨.

22．（1）证明：由消去y得，

①.判别式二次方程①有两个不等实根，是方程组不同的解，的图象交于两个不同的点.

（2）与图象的两交点分别位于直线的两侧，等价于方程 的一根小于1，另一根大于1.

　，一个根小于1，另一个根大于1.

　　的图象的两个交点分别位于直线x=1的两侧.

（3）设方程的两根为那么线段AB在x轴上的射影长为