高三统一考试数学卷
数 学 试 题(理工农医类)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟.
第Ⅰ卷(选择题 共60分)
参考公式:
如果事件A、B互斥,那么 正棱锥、圆锥的侧面积公式
P(A+B)=P(A)+P(B)
![]()
如果事件A、B相互独立,那么
其中![]() 表示底面周长,
表示底面周长,![]() 表示斜高或母线长
表示斜高或母线长
P(A·B)=P(A)·P(B) 球体的体积公式
如果事件A在一次试验中发生的概率是P,那 ![]()
么n次独立重复试验中恰好发生k次的概率 其中R表示球的半径
![]()
一、选择题:本大题共12个小题;每小题5分,共60分,在每小题给出的四个选项中, 只有且只有一项是符合题目要求的.
1.若U是全集,A是U的一个真子集,则下列结论中错误的是 ( )
|
|
C. U![]() D. U
D. U ![]() Φ
Φ
|
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.双曲线![]() 的一条准线方程是
的一条准线方程是![]() ,则
,则![]() 应等于 ( )
应等于 ( )
A.-4 B.-2 C.-![]() D.-
D.-![]()
4.一次测量中出现正误差和负误差的概率都是![]() ,在5次测量中恰好出现2次正误差的概率是 ( )
,在5次测量中恰好出现2次正误差的概率是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.等比数列{![]() }的首项
}的首项![]() ,前
,前![]() 项和为
项和为![]() ,若
,若![]() ,则
,则![]() 等于 ( )
等于 ( )
A.![]() B.-2 C.2 D.-
B.-2 C.2 D.-![]()
6.长方体ABCD—A1B1C1D1中,AA1=A1D1=1,AB=2,E为AB的中点,则C1到平面D1DE的距离为 ( )
A.![]() B.1 C.
B.1 C.![]() D.
D.![]()
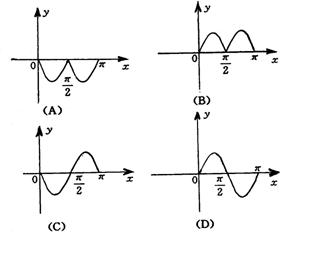
7.若函数![]() 在区间[
在区间[![]() ]上单调递增,则函数
]上单调递增,则函数![]() 可以是( )
可以是( )
A.![]() B.-
B.-![]() C.1 D.
C.1 D.![]()
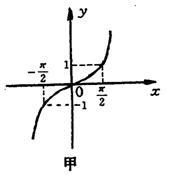
8.在![]() 四个函数中,当
四个函数中,当![]() 时,使
时,使![]() 成立的函数有 ( )
成立的函数有 ( )
A.0个 B.1个 C.2个 D.3个
9.编号1,2,3,4,5,6的六个球分别放入编号为1,2,3,4,5,6的六个盒子中,其中有且只有三个球的编号与盒子的编号一致的放法种数有 ( )
A.20 B.40 C.120 D.480
10.若以![]() 上任一点P为圆心作与直线
上任一点P为圆心作与直线![]() 相切的圆,那么这些圆必定过平面内的点 ( )
相切的圆,那么这些圆必定过平面内的点 ( )
A.(0,1) B.(-1,0) C.(0,-1) D.(-1,-1)
11.已知![]() 是两条直线,
是两条直线,![]() 是两个平面,有下列4个命题:
是两个平面,有下列4个命题:
①若![]() ,则
,则![]()
②若![]() ,则
,则![]()
③若![]() 则
则![]()
④若![]() 异面,
异面, ![]() ,则
,则![]() .
.
其中正确命题有 ( )
A.①② B.②③ C.③④ D.②④
|
|
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分. 把答案填在题中横线上.
13.不等式![]() 的解集为
.
的解集为
.
14.某工厂一个班组共有5个男工,3个女工,现要选3个代表去先进单位参观学习,则3个代表中至少有一个女工的概率是 .
|
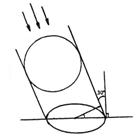
16.如图,一球形广告气球被一束入射角为30°
的平行光线照射,其投影是一个长半轴为
5 米的椭圆,则制作这个广告气球至少需
要的面料是
米2(![]() 取3.2)
取3.2)
三、解答题:本大题共6小题,共74分. 解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)
在△ABC中,∠A、∠B、∠C对边分别为![]() 、
、![]() 、
、![]() ,已知
,已知![]() ,且最长边为
,且最长边为![]() .
.
(Ⅰ)求A;
(Ⅱ)求△ABC最短边的长.
注意:考生在(18甲)、(18乙)两题中选一题作答,如果两题都答,只以(18甲)计分.
18.(本小题满分12分)
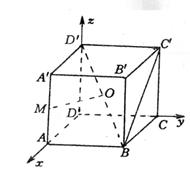
(甲)如图建立直角坐标系,已知正方体ABCD—![]() 的棱长为
的棱长为![]() ,M是棱
,M是棱![]() 的中点,点O是对角线
的中点,点O是对角线![]() 的中点.
的中点.
|
(Ⅱ)求异面直线MO和![]() 所成的角的大小.
所成的角的大小.
18(本小题满分12分)
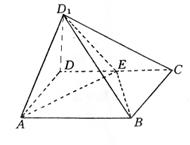
(乙)如图矩形ABCD中,AB=2BC,E为CD的中点.将矩形沿AE折成二面角D1—AE—B,使BD1=CD1.
|
(Ⅱ)求异面直线AE与CD1所成的角.
19.(本小题满分12分)
已知公差大于零的等差数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足:
,且满足:![]()
(Ⅰ)求通项![]() ;
;
(Ⅱ)若数列![]() 是等差数列,且
是等差数列,且![]() ,求非零常数
,求非零常数![]() ;
;
(Ⅲ)求![]() 的最大值.
的最大值.
20.(本小题满分12分)
某工厂有216名工人接受了生产1000台GH型高科技产品的总任务,已知每台GH型产品由4个G型装置和3个H型装置配套组成. 每个工人每小时能加工6个G型装置或3个H型装置. 现将工人分成两组同时开始加工,每组分别加工一种装置. 设加工G型装置的工人有![]() 人,他们加工完G型装置所需时间为
人,他们加工完G型装置所需时间为![]() ,其余工人加工完H型装置所需时间为
,其余工人加工完H型装置所需时间为![]() (单位:小时,可不为整数).
(单位:小时,可不为整数).
(Ⅰ)写出![]() 解析式;
解析式;
(Ⅱ)比较![]() 与
与![]() 的大小,并写出这216名工人完成总任务的时间
的大小,并写出这216名工人完成总任务的时间![]() 的解析式;
的解析式;
(Ⅲ)应怎样分组,才能使完成总任务用的时间最少?
21.(本小题满分12分)
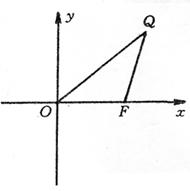
已知![]() 的面积为S,且
的面积为S,且![]() 建立如右图所示的直角坐标系.
建立如右图所示的直角坐标系.
(Ⅰ)若![]() ,求向量
,求向量![]() 所在直线方程;
所在直线方程;
|
22.(本小题满分14分)
已知平面向量![]()
(Ⅰ)证明:![]() ;
;
(Ⅱ)若存在不为零的实数![]() ,
,![]() ,使得
,使得![]() 且
且![]() ,试求函数
,试求函数![]() 的表达式;
的表达式;
(Ⅲ)当![]() 时,是否存在不小于2的常数
时,是否存在不小于2的常数![]() ,使
,使![]() 有最大值12?若存在,求出
有最大值12?若存在,求出![]() 值;若不存在,说明理由.
值;若不存在,说明理由.
高 三 统 一 考 试
数 学 试 题(理工)参考答案及评分标准
一、选择题:本题考查基本知识的基本运算,每小题5分,满分60分.
DCCAD AABBC BD
二、填空题:本题考查基本知识和基本运算,每小题4分,满分16分.
13.[-2,1] 14.![]() 15.
15.![]() 16. 240
16. 240
三、解答题:本大题共6小题,共74分.
17.(本小题满分12分)
解:(Ⅰ)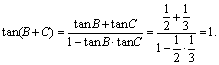 ……3分 在△ABC中,
……3分 在△ABC中,![]()
![]() 则
则![]() ……6分
……6分
(Ⅱ)由题意知,∠C对边最短,∠A对边最长. ![]() 又
又
![]() C为锐角,
C为锐角,![]() ……9分
……9分
由正弦定理,得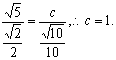 即△ABC最短边的长为1.……12分
即△ABC最短边的长为1.……12分
18.(甲)(本小题满分12分)
(Ⅰ)证明:![]()
![]() ……4分
……4分
![]() ∴OM是异面直线
∴OM是异面直线![]() 和
和![]() 的公垂线.……8分
的公垂线.……8分
|
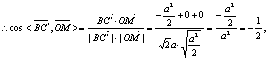
![]() ∴异面直线OM和
∴异面直线OM和![]() 所成的角为60°.……12分
所成的角为60°.……12分
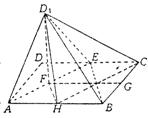
18.(乙)(Ⅰ)证明:取AE中点F,BC中点G,连结D1F,FG,D1G.
由题意知,AD1=D1E,BD1=CD1,
∴D1F⊥AE,D1G⊥BC. FG⊥BC,∴BC⊥平面D1FG ,……3分 ∴BC⊥D1F, 又D1F⊥AE,AE与BC相交,∴D1F⊥平面ABC,∴平面AD1E⊥平面ABC.……5分
(Ⅱ)解:取AB中点H,连结CH,则CH//AE,∴ ∠D1CH即为AE与CD1所成的角. ……6分
连结D1H,CF,HF. ∵D1F⊥平面ABC,D1F⊥CF, D1F⊥FH. 设AB=![]() ,∴△CEF中,
,∴△CEF中,
![]()
在Rt△D1CF中,![]()
在Rt△D1FH中,![]() ……10分
……10分
在△D1CH中,![]()
![]() ∴所求角的大小是
∴所求角的大小是![]() .……12分
.……12分
(注:也可先证CH⊥D1H)
19.(本小题满分12分) 解:(Ⅰ)![]() 为等差数列,
为等差数列,![]() 又
又![]() =117,
=117,![]() 是方程
是方程![]() 的两实根.又公差
的两实根.又公差![]()
![]()
∴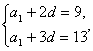 ∴
∴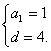
![]() ……4分
……4分
(Ⅱ)由(Ⅰ)知![]() ……6分
……6分
![]()
![]() 是等差数列,
是等差数列, ![]()
即![]() 舍去.) 故
舍去.) 故![]() ……8分
……8分
(Ⅲ)由(Ⅱ)得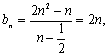 ……9分
……9分
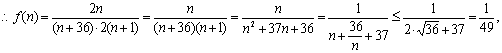
当且仅当![]() 即
即![]() 时取等号,
时取等号,![]() 即
即![]() 的最大值为
的最大值为![]() ……12分
……12分
20.(本小题满分12分)解:(Ⅰ)由题意知,需加工G型装置4000个,加工H型装置3000个,所用工人分别为![]() 人,
人,![]() 人.
人. ![]()
即![]() ……3分
……3分
(Ⅱ)![]() ……4分
……4分
![]()
当![]() ;
;
当![]() ……6分
……6分
![]()
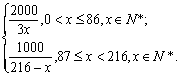 ……8分
……8分
(Ⅲ)完成总任务所用时间最少即求![]() 的最小值.
的最小值.
当![]() 时,
时,![]() 递减,
递减,![]()
![]() 此时
此时![]() 当
当![]() 时,
时,![]() 递增,
递增,
![]()
![]() 此时
此时![]()
![]() ∴加工G型装置,H型装置的人数分别为86,130或87,129.……12分
∴加工G型装置,H型装置的人数分别为86,130或87,129.……12分
21.(本小题满分12分)解:(Ⅰ)设Q(![]()
![]()
![]() …2分
…2分
![]()
![]() ……4分
……4分
![]() 所在直线的方程为
所在直线的方程为![]() 或
或![]() ……5分
……5分
(Ⅱ)设![]()
![]() 又
又![]()
![]() ……7分 令
……7分 令![]()
![]() 在[2,+∞]上递增,
在[2,+∞]上递增,![]() 此时
此时
![]() 取最小值,
取最小值,![]() ……10分 由题意,设椭圆方程
……10分 由题意,设椭圆方程
![]() 则
则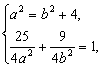 解得
解得![]()
故椭圆方程![]() ……12分
……12分
22.(本小题满分12分)解:(Ⅰ)证明:![]() ……2分
……2分
(Ⅱ)解:![]()
而![]() …4分
…4分![]()
即![]() ……6分
……6分
(Ⅲ)若存在![]() 满足条件,则
满足条件,则![]() 由
由![]()
当![]() 时,
时,![]() 在[0,
在[0,![]() ]上递增;
]上递增;
当![]() 时,
时,![]() 在[
在[![]() ,+∞
,+∞![]() 上递减.……9分
上递减.……9分
①若![]() 即
即![]() 时,
时,![]()
![]() 不存在满足条件的
不存在满足条件的![]() 值.……11分
值.……11分
②若![]() 即
即![]() 时,
时,![]() 在[0,1]上递增,
在[0,1]上递增,![]()
![]()
![]() 满足条件.……12分
满足条件.……12分
综上,当![]() 时,存在不小于2的常数
时,存在不小于2的常数![]() 使
使![]() 的最大值12.……14分
的最大值12.……14分