高三一轮复习验收考试数学试题（文理）

高三一轮复习验收考试数学试题（文理）

　

第Ⅰ卷（选择题，共60分）

注意事项：1.本试卷分第Ⅰ卷和第Ⅱ卷两部分。第Ⅰ卷为选择题，60分；第Ⅱ卷为非选择题，90分；共150分，考试时间为120分钟。

2.选择题答案用2B铅笔在答题卡上把对应题目答案标号涂黑。

一、.选择题：本大题共12小题，每小题5分，共60分。　　　　　　　　　　　　　　　　

（1）设集合若，则与集合M,N的关系是（　 ）

A.　 　 B.　　 　　 C.　 　 D.　

（2）已知函数。设当y取得最大值时角x的值为α，当y取得最小值时角x的值为β，其中α，β均属于区间[]，则的值等于（　 ）　

　 A.　　 B.　　C.　0　 D.　　　　　　　　　

（3）有等式x⁴+a₁x³+a₂x²+a₃x+a₄=(x+1)⁴+b₁(x+1)³+b₂(x+1)²+b₃(x+1)+b₄，定义映射f∶(a₁,a₂,a₃,a₄)→(b₁,b₂,b₃,b₄)，则f (4,3,2,1)等于（　）

　A （1,2,3,4）　　 B.（0,3,4,0）　　C. （-1,0,2,-2）　　D.　 (0,-3,4,-1)

（4）表示α,β表示平面，m, n表示直线，则m∥α的一个充分必要条件是（　）

A.α⊥β且m⊥β　　　 B.α∩β=n 且 m∥n

C.m∥n 且 n∥α　　　　D.α∥β且

（5）设，且，则锐角α为

A.　30º　　 B.60º　　 C.45º　　　D.75º

（6）设是一个整数，且，给出下列四个结论：

① ⑵③0<a<b<1　　　④ab-1=0

其中正确结论的个数是（　 ）

A.1　  B.2　　 C.3　　 D.4

（7）已知函数f(x)的定义域为R,且对于任意实数a，f^-1(x+a)与f(x+a)互为反函数，若f(1)=2,则f(2)的值为（　）

A.0　　 B.　 1　　C.　2　　　D.　3

（8）等比数列{a_n}中，a₁+a₂,=30, a₃+a₄=60 ,则a₇+a₈的值为（　 ）

A.　240　　　B.　　-240　　 C.　　 ±240　　 D.　　1920

（9）设函数f(x)的定义域为R,且f(-x)=-f(x)，当x∈(0, +∞)时,f(x+d)>f(x),(d>0)若f(-2)=0，则xf(x)<0的解集为（　）

A.Φ　　　B.(-2, 0)　　C.(0, 2)　 D(-2, 0)∪(0, 2)

（10）从5个数1,2,3,4,5中任取3个数x₁, x₂, x₃ ，y表示x₁, x₂, x₃中最大的一个，则y 的分布列为(　　)

A.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  　　　B.　　　

η	1	2	3	4	5
p

η	3	4	5
p

　C.　　　　　　　　　　　　　　　　　  D.

η	1	2	3	4	5
p

η	3	4	5
p

（11）平面内有一长度为4 的线段AB,动点P满足PA+PB=6,则PA的取值范围是（　 ）

A.　 [1,5]　　　B[1,6]　　　C.[2, 5]　　　 D.[2,6]

（12）如图，在一块矩形的草地上（矩形的水平方向为b米，竖直方向为a米），一条弯曲的柏油小路（小路的任何地方的水平宽度都是1米）。则草地剩余部分的面积为（　）

A.大于（ab-a) 平方米　　　　　　  B.小于(ab-a)平方米

C.等于（ab-a） 平方米　　　　　　　　　　　　　　　  D.不确定

　　　

 

第Ⅱ卷（非选择题，共90分）

题号	二	三						总分
		17	18	19	20	21	22
分数

二、填空题：本大题共4 小题，每小题4分，共16分，把答案填在题中横线上。

（13）两个腰长均为1的等腰直角三角形ABC和等腰直角三角形ABD所在的平面构成60°的二面角，则点C和点D之间的距离等于_______________________________.（写出所有可能的值）

（14）已知关于x的不等式(a²-4)x²+(a+2)x-1≥0的解集是空集，则实数a的取值范围是_____________.

（15）若函数，则当自变量x取1,2,3,……，100这100个自然数时，函数值的和是_____________.

（16）抛物线y²=2px过点A（2,4），F是其焦点，又定点B的坐标为（8,-8）。那么AF∶BF的值为_____________。

三、解答题：本大题共6小题，共74分。

（17）（本小题满分12分）

已知且sinβcscα=cos(α+β), 当tanβ取最大值时，求cot(α+β)的值

（18甲）（本小题满分12分）

如图直三棱柱ABC─A₁B₁C₁，底面ΔABC中，CA=CB=1,∠BCA=90°， AA₁=2,MN分别是A₁B₁、A₁A的中点。

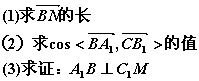
（18乙）（本小题满分12分）

长方形ABCD的长AB是宽BC的倍，把它折成无底面的正三棱柱，使AD与BC重合，折痕线EF，GH分别交对角线AC与M，N。求折后截面AMN与底面AFH所成的角。

（19）（本小题满分12分）

有一种“摸彩”的赌博游戏，庄家（赌主）在一个袋子里装有大小相同的8只白球和8只黑球，从中任意摸出5只球，中彩情况如下表：

摸到	恰5个同色球	恰4个同色球	其它
彩金	25元	5元	谢谢参与（未中奖）

摸奖一次付费2元。

试计算：（1）能获得25元彩金的概率和获得5元彩金的概率；

　　　 （2）在1000次的摸奖中，庄家大约能赚多少钱？

（20）（本小题满分12分）

数列{a_n}的前n项和为S_n=2ⁿ+p(p∈R)，数列{b_n}满足b_n=log₂a_n,若数列{a_n}为等比数列。

（1）求p的值及通项a_n。

（2）求和T_n=(b₁)²-(b₂)²+(b₃)²-　……+(-1)ⁿ⁺¹(b_n)²（n∈N)

（21文）（本小题满分12分）

直线y=kx+1与双曲线x²-y²=1的左支交与A、B两点，直线 l 经过点（-2,0)和AB中点，求直线 l 在y轴上的截距b的取值范围。

（21理）（本小题满分12分）

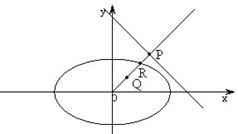
已知椭圆，直线，P是 l 上一点，OP射线交椭圆与点R,又点Q在OP上，且满足OQ·OP=OR²,当P在l上移动时，求点Q的轨迹方程，并说明轨迹是什么曲线。

22）（本小题满分14分）

已知a>0,函数f(x)＝x³-ax在区间[1,+ ∞)上是单调增函数。

（1）求a实数的取值范围；

（2）设x₀≥1，f(x₀)≥1,且f[f x₀)]= x₀，求证:f(x₀)= x_0。

高三一轮复习验收考试

数学试题（文理）参考答案　 2004.3

一、选择题：CBDDC　 ABADB　 AC

二、填空题：（13） （14）　 （15）390　（16）

三、解答题：

（17）解：

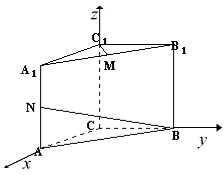
（18甲）解：如图，以C为原点建立空间直角坐标系O─xyz 

（1）依题意得：B（0,1,0），N（1,0,1）　　

（2）依题意得：A₁（1,0,2），C（0,0,0）

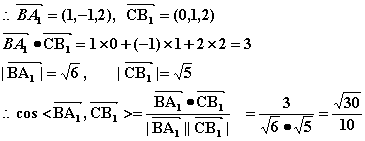
（3）依题意得：C₁（0,0,2），　M

　

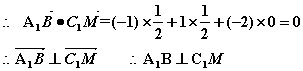
(18乙) 解:

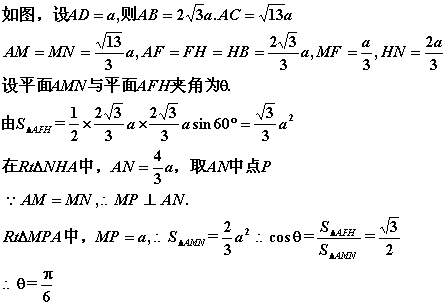
（19）解：

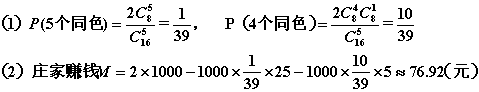
（20）解：

∵数列{a_n}为等比数列，前n项和为S_n=2ⁿ+p(p∈R)，故P=-1;即a₁=1,q=2,　　∴a_n=2^n-1.

(2) ∵b_n=log₂a_n=n-1, ∴当n=2k(k∈N^*)时,

T_n=(b₁)²-b₂)²+（b₃)²--……+(-1)^n-1(b_n）²

=(b₁+b₂) (b₁-b₂)+ (b₃+b₄) (b₃+b₄)+ ……+ (b_2k-1+b_2k) (b_2k-1+b_2k)

=-[1+2+3+……(2k-1)]=-2k²+k,当n=2k+1(k∈N)时，可得

T_n=2k²+k

(21文)解：

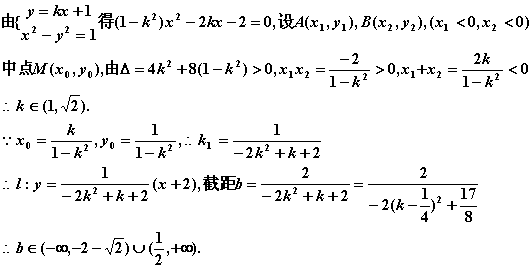
（21理）解：

（22）解：（1）∵f(x)在[1,+∞)是增函数，∴在（1,+∞)恒有f´(x)>0.

又f´(x)=3x²-a, ∴3x²-a>0, ∴a<3x²，又x∈(1,+∞),3x²∈（3,+∞)

∴0<a≤3

(1)　法二：任取x₁ ,x₂∈[1,+∞),且x₁ <x₂，则

f(x₁)-f(x₂)=(x₁³-ax₁)- (x₂³-ax₂)=(x₁-x₂)(x₁²+x₁x₂+x₂²-a)

显然不会存在常数a，使(x₁²+x₁x₂+x₂²-a)恒为负值，而f(x)有确定单调性，从而必有一个常数a，使(x₁²+x₁x₂+x₂²-a)恒为正值，

即x₁²+x₁x₂+x₂²>a，∴a≤3这时有f(x₁)<f(x₂)

即f(x)在[1,+∞)上是递增函数，故所求实数的取值范围是（0，3].

(2)　  采用反证法。假设f(x₀)≠x₀, ∵f(x)在[1,+∞)是增函数

∴当f(x₀)>x₀ 时，有f[f(x₀)]>f(x₀)，即f[f(x₀)]>x₀，这与已知 f[f(x₀)]=x₀矛盾。

 当f(x₀)<x₀ 时，有 f[f(x₀)]<f(x₀)，即f[f(x₀)]<x₀，这与已知f[f(x₀)]=x₀矛盾。

∴f(x₀)=x₀