高三数学第二次月考试题
数 学(文史类)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页.第Ⅱ卷3至8页.共150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用像皮擦干净后,再选涂其它答案,不能答在试题卷上.
3.考试结束,监考人将本试卷和答题卡一并收回.
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若函数![]() 的定义域P=
的定义域P=![]() 是,则该函数的值域是( )
是,则该函数的值域是( )
 A.
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
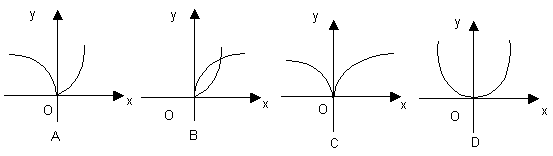
2.函数![]() 的图象大致是( )
的图象大致是( )
3.数列![]() 是公差为-2的等差数列,若
是公差为-2的等差数列,若![]() ,则
,则![]() 的值是( )
的值是( )
A.-182 B.-78 C.-148 D.-82
4.已知![]() 在
在![]() 上的单调递增,则( )
上的单调递增,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知![]() 是奇函数,定义域为
是奇函数,定义域为![]() ,又
,又![]() 在区间
在区间![]() 上是增函数,且
上是增函数,且![]() ,满足
,满足![]() 的
的![]() 取值范围是( )
取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.不等式![]() 的解集是( )
的解集是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.某地每年消耗20万立方米,每立方米木材的价格是240元,为了减少木材消耗,政府决定按t%征收木材税,这样每年的木材消耗量就减少![]() 万立方米,为了既减少木材消耗又保证税金收入每年不少于90万元,则
万立方米,为了既减少木材消耗又保证税金收入每年不少于90万元,则![]() 的范围是( )
的范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.已知定义在R上的偶函数![]() 在
在![]() 上是增函数,且
上是增函数,且![]() ,则满足
,则满足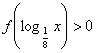 的
的![]() 取值范围是( )
取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.若不等式![]() 在开区间
在开区间![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.已知函数![]() 的导数为
的导数为![]() ,且图象过点
,且图象过点![]() ,当函数
,当函数![]() 的取得极大值-5时,
的取得极大值-5时,![]() 的值应为( )
的值应为( )
A.-1 B.0 C.1 D.![]()
11.做一个面积为1平方米,形状为直角三角形的铁架框,有下列四种长度的铁管,最合理的(既够用,又浪费最少)的是( )
A.4.6米 B.4.8米 C.5米 D.5.2米
12.国际上通用恩格尔系数来衡量一个国家和地区人民生活水平的状况,它的计算公式![]() (
(![]() :人均食品支出总额,
:人均食品支出总额,![]() :人均个人消费支出总额)。且
:人均个人消费支出总额)。且![]() 。
。
各类型家庭
| 家庭类型 | 贫困 | 温饱 | 小康 | 富裕 |
| n | n≥59% | 50%≤n≤59% | 40%≤n≤50% | 30%≤n≤49% |
李先生居住地2002年比1998年食品下降了7.5%,该家庭2002年购买食品和1998年完全相同的情况下人均少支出了75元,该家庭2002年属于( )
A.贫困 B.温饱 C.小康 D.富裕
第二次月考试题
数 学(文史类)
第Ⅱ卷(非选择题共90分)
注意事项:
1.第Ⅱ卷共6页,用钢笔或圆珠笔直接答在试题卷中.
2.答卷前将密封线内的项目填写清楚.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
| 题 号 | 二 | 三 | 总 分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | |||
| 分 数 | ||||||||
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
13.方程log![]()
![]() =
=![]() 的解集是 。
的解集是 。
14.已知函数![]() ,若
,若![]() ,则数列
,则数列![]() 的通项公式是 。
的通项公式是 。
15.设![]() ,那么
,那么![]()
![]()
![]() 的值为 。
的值为 。
16.设有两个命题:(1)不等式![]() 对于一切实数
对于一切实数![]() 恒成立;(2)函数
恒成立;(2)函数![]() 是R上的减函数,如果这两个命题都是真命题,则的取值范围是 。
是R上的减函数,如果这两个命题都是真命题,则的取值范围是 。
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
| 得分 | 评卷人 |
(17)(本小题满分12分)已知函数![]() 在定义域
在定义域![]() 上是减函数,且
上是减函数,且![]() .(Ⅰ)求
.(Ⅰ)求![]() 的取值范围;(Ⅱ)解不等式
的取值范围;(Ⅱ)解不等式![]() .
.
| 得分 | 评卷人 |
(18)(本小题满分12分)
已知等差数列![]() 的前项和为
的前项和为![]() ,且
,且![]() ,
,![]() ,又设
,又设![]() ,其中常数
,其中常数![]() 满足
满足![]() ,试求数列
,试求数列![]() 的通项公式。
的通项公式。
| 得分 | 评卷人 |
(19)(本小题满分12分)已知函数![]() 是奇函数,且
是奇函数,且![]() (Ⅰ)求
(Ⅰ)求![]() 的值;(Ⅱ)当
的值;(Ⅱ)当![]() 时,讨论函数
时,讨论函数![]() 的单调性(写出证明过程)。
的单调性(写出证明过程)。
| 得分 | 评卷人 |
(20)(本小题满分12分)某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品![]() (百台),其总成本为
(百台),其总成本为![]() (万元),其中固定资本为2万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本);销售收入为
(万元),其中固定资本为2万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本);销售收入为![]() (万元)满足
(万元)满足
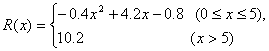 假设该产品产销平衡,那么根据上述统计规律。
假设该产品产销平衡,那么根据上述统计规律。
(Ⅰ)要使工厂有赢利,产量应该控制在什么范围?
(Ⅱ)工厂生产多少台产品时,可使赢利最多?
(Ⅲ)求赢利最多时每台产品的售价.
| 得分 | 评卷人 |
(21)(本小题满分12分)在直角坐标系中,设矩形的顶点OPQR按逆时针顺序依次为O![]() 、P
、P![]() 、Q
、Q![]() 、R
、R![]() ,其中
,其中![]()
(Ⅰ)求矩形在第一象限部分的面积;(Ⅱ)讨论函数的单调性。
| 得分 | 评卷人 |
(22)(本小题满分14分)
设二次函数![]()
(Ⅰ)若![]() ,试求
,试求![]() 的解析式,并求
的解析式,并求![]() 的最小值;
的最小值;
(Ⅱ)若![]() 是函数
是函数![]() 的极值,且
的极值,且![]() 的图像在
的图像在![]() 轴上截得的弦长不小于2,试分别求
轴上截得的弦长不小于2,试分别求![]() 、
、![]() 的符号;
的符号;
(Ⅲ)在(Ⅱ)的条件下,是否存在实数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上是单调函数?若存在,请求出实数
上是单调函数?若存在,请求出实数![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
参考答案:
一、AD,DCBAB,CD 二、13、![]() 14、
14、![]() 15、5 16、
15、5 16、![]()
三、17、(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() 18、
18、![]() 19(Ⅰ)a=1,b=1,c=0(Ⅱ)在
19(Ⅰ)a=1,b=1,c=0(Ⅱ)在![]() 是减函数,在
是减函数,在![]() 是增函数 20(Ⅰ)
是增函数 20(Ⅰ)![]() (Ⅱ)3.6万元(Ⅲ)240元 21 (Ⅰ)
(Ⅱ)3.6万元(Ⅲ)240元 21 (Ⅰ)![]() (Ⅱ)在为减函数 22.(Ⅰ)
(Ⅱ)在为减函数 22.(Ⅰ)![]() (Ⅱ)b<0,c<0(Ⅲ)不存在。
(Ⅱ)b<0,c<0(Ⅲ)不存在。