高三数学第二学期期末考试

高三数学第二学期期末考试

　　　　　　　　　　　　　 数　　学　　　　　　　　 

校名　　　　　 　 班级　　　　  　　 姓名___________

参考公式：

　　三角函数的积化和差公式

sinαcosβ=　　　　球冠面积Ｓ＝2πRh

sinαcosβ=　　　　 其中Ｒ表示球的半径；

cosαcosβ=　　　　  h表示球冠的高

sinαcosβ=　　　　

一、选择题：本大题共14小题；第（１）一（10）题每小题４分，第（11）－（14）题每小题５分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.

 （１）sin15°cos165°的值等于　　　　　　　　　　　　　　　　　　　  （ ）

　　 （Ａ）　　   （Ｂ）　　　　 （Ｃ）　　 （Ｄ）

 （２）双曲线的渐近线方程是　　　　　　　　　　　　　　  （ ）

　　 （A）　 （B）　　（C）  （D）

（３）设集合，那么集合Ｍ与Ｎ之间的关系是　　　　　　 （　）

　　 （Ａ）　　（Ｂ）M=N　 （Ｃ）　 （Ｄ）

 （４）４名男生２名女生站成一排，要求两名女生分别站在两端，则不同排法的种数为（ ）

　　 （Ａ）48　　 （Ｂ）96　 （Ｃ）144　 （Ｄ）288

（５）已知复数z=(t+i)²的辐角主值是，则实数t的值是　　　　　　　 （ ）

　　 （Ａ）0　　　（Ｂ）-1　　（Ｃ）1　　 （Ｄ）不能确定

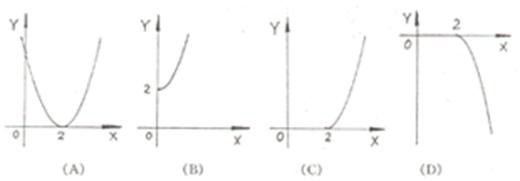
（６）函数f(x)=的反函数f^—1(x)是图象是　　　　　　　　　  （ ）

　　　　　　　　　　　 

（７）理料做：在极坐标系中，点Ａ在曲线上，点Ｂ在曲线上，则的最小值为　　　　　　　　　　　　　　　　　　　　　　　　　　　  （ ）

　　（Ａ）０　　 （Ｂ）　　 （Ｃ）　　　　　　 （Ｄ）１

文科做：已知函数，４]上是减函数，那么实数 a的取值范围是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （ ）

　　（Ａ）a≥–3　　　 （Ｂ）a≤–3　　 （Ｃ）a≤5　　（Ｄ）a≥3

（８）已知，则的值等于（ ）

　　（Ａ）64　　　　 （Ｂ）32　　　　  （Ｃ）63　　　　 （Ｄ）31

（９）理科做：直线　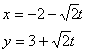 (t为参数)上到点Ａ（－２，３）的距离等于 的一个点的坐标是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  （ ）

　　（Ａ）（－２，３）　　　　　　　　　　　  （Ｂ）（－４，５）

　　（Ｃ）（）　　　　　　　　 （Ｄ）（－３，４）

　 文科做：若k可以取任何实数，则方程x²+ky²=1所表示的曲线不可能是（ ）

　　（Ａ）直线　　（Ｂ）圆　　　 （Ｃ）椭圆或双曲钱　　（Ｄ）抛物线

（10）的必要但不充分条件是　　　　　　　　　　　　　　　　  （ ）

　　（Ａ）　（Ｂ）　 （Ｃ）　 （Ｄ）

（11）已知集合及

，则实数b的取值范围是（ ）

　　（Ａ）[–5,5]　　（Ｂ）　　 （Ｃ）　　（Ｄ）

（12） a、b是异面直线，以下面四个命题：

　　①过a至少有一个平面平行于b　　　②过a至少有一个平面垂直于b

　　③至多有一条直线与a、b都垂直　　 ④至少有一个平面分别与a、b都平行

其中正确命题的个数是　　　　　　　　　　　　　　　　　　　  （ ）

　　（Ａ）０　　　 （Ｂ）１　　　（Ｃ）２　　  （Ｄ）３

（13）直线y=x cosα+1（）的倾斜角的取值范围是　　　　　　　　　 （ ）

　　（Ａ）　　　　　　　   （Ｂ）[0,π]

　　（Ｃ）　　　　　　　  （Ｄ）

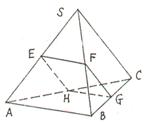
（14）三棱锥Ｓ－ABC,Ｅ、F、G、Ｈ分别是棱SA、SB、

BC、AC的中点，截面EFGH将三棱锥分割为两个几何

体：AB－EFGH、SC－EFGH，将其体积分别是V₁、V₂，

则V₁∶V₂的值是　 (　)

　　（Ａ）１∶２　 （Ｂ）１∶３　　（Ｃ）２∶３　　（Ｄ）１∶１

二、填空题：本大题共４小题；每小题４分，共16分，把答案填在题中横钱上.

（15）设等差数列共有3n项，它的前2n项之和是100，后2n项之和是200，则该等差数列的中间n项之和等于　　　　　　　　　 .

（16）以椭圆的中心Ｏ为顶点，以椭圆的左准线为准线的抛物线与椭圆的右准线交于Ａ、Ｂ两点，则的值为　　　　　　 .

（17）若的值等于　　　　　　　 .

（18）人造地球同步通讯卫星的运行轨道是圆，卫星距地面高度是19200km地球半径取6400km，若电磁波是直线传播，那么卫星覆盖的地球表面区别（是一个球冠）的面积与地球表面积之比是　　　　　 .

三、解答题：本大题共６小题；共74分，解答应写出文字说明、证明过程或演算步骤.

（19）（本小题满分12分）

在△ABC中，∠Ａ、∠Ｂ、∠Ｃ所对的边分别为a、b、c，且a、b、3c成等比数列，又

∠Ａ－∠Ｃ.　　 试求∠Ａ、∠Ｂ、∠Ｃ的值.

（20）（本小题满分10分）

理科作：已知两个复数集合，

，求实数λ的取值范围.

文科作：设函数f(x)的定义域为Ｒ，且在其定义域Ｒ上，总有f(x)=–f(x+2)，又当

–1<x≤1时，f(x)=x²+2x.

（Ⅰ）求当3<x≤5是， 函数f(x)的解析式.

（Ⅱ）试判断函数f(x)在（３，５]上的增减性,并予以证明.

（21）（本小题满分14分）

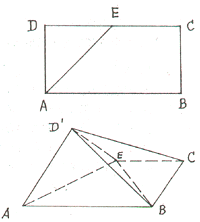
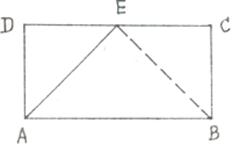
如图：矩形ABCD,AB=2AD=2a，E是CD边的中点，

以AE为棱，将△DAE向上折起,将D变到D'的位置,

使面D'AE与面ABCE成直二面角.

（Ⅰ)求直线D'B与平面ABCE所成的角的正切值；

（Ⅱ）求证：AD'⊥BE；

（Ⅲ）求四棱锥Ｄ'－ABCE的体积；

（Ⅳ）求异面直线AD'与BC所成的角.

（文科学生只作（Ⅰ）、（Ⅱ）、（Ⅲ））

（22）（本小题满分12分）

无穷等比数列的首项a₁=1，其公比q为实常数，且，数列的前n项和为S_n且其各项和为Ｓ，数列的前n项和为T_n.

（Ⅰ）求T_n.(将T_n写成关于q的表达式)

（Ⅱ）求.（写成关于q的表达式）

（23）（本小题满分12分）

某隧道长a米，最高限速为米／秒，一个匀速行进的车队有10辆车，每辆车长为l米，相邻两车之间距离m（米）与车速υ（米／秒）的平方成正比,比例系数为k,自第1辆车车头进隧道至第10辆车车尾离开隧道时所用的时间为t秒.

（Ⅰ）求出函数t=f(υ)的解析式，并求定义域；

（Ⅱ）求车队通过隧道时间t的最小值，并求出t取得最小值时υ的大小.

（24）（本小题满分14分）

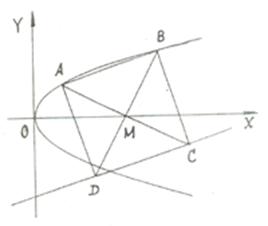
设正方形ABCD的外接圆方程为x²+y²–6x+a=0(a<9)，Ｃ、Ｄ点所在直线l的斜率为 .

（Ⅰ）求外接圆圆心Ｍ点的坐标及正方形对角线AC、BD的斜率；

（Ⅱ）理科作：如果在x轴上方的Ａ、Ｂ两点在一条以原点为顶点，以x轴为对称轴的抛物线上，求此抛物线的方程及直线l的方程.

　　文科作：如果ABCD的外接圆半径为,在x轴上方的Ａ、Ｂ两点在一条以x轴为对称轴的抛物线上，求此抛物线的方程及直线l的方程.

高三数学期末考试参考答案与评分标准

一、选择题：

（１）Ｂ（２）Ｄ（３）Ａ（４）Ａ（５）Ｃ（６）Ｃ（７）理Ａ文Ｂ（８）Ｂ

（９）Ｄ（10）Ａ（11）Ｃ（12）Ｂ（13）Ｄ（14）Ｄ

二、填空题：　　

（15）75　　（16）　　  （17）　　（18）3∶8

三、解答题：

（19）本题满分12分

解：由a,b,3c成等比数列，得b²=(3c)·a=3ca　　　　  　　　　　　　 …………2分

依正弦定理，sin²B=3sinC·sinA　　　　　　　　　　　 　　　　　　　 …………4分

于是　　

　　　 …………６分

即

化简得：

只能　　　　　　　　　　　　　　　　　　　　 　　 …………８分

　　　　　　　　　　　　　　　  　　 …………10分

再依条件　　　　　 …………12分

（20）本题满分10分

　　　理科作：

解：由已知，集合Ｍ、Ｎ中至少有一相等元素，可得：

　　　　　　　　　　　　　　　　  …………2分

由复数相等的定义得：

　　　cosθ=m

　　　4-m²=λ+sinθ　　　　　　　　　　　　　　　　　　　  　　　　…………4分

则：λ=4–cos²θ–sinθ

　　　=sin²θ–sinθ+3

　　　=　　　　　　　　　　　　　　　　　　　 　　 …………7分

当sinθ=　　　　 　　 …………8分

另一方面，当sinθ=–1　即　　　　  …………９分

故：　　　　　　　　　　　　　　　　　　　　　　　　　　…………10分

文科作：

（Ⅰ）解：∵f(x+4)=f[(x+2)+2]=-f(x+2)=f(x)　　　　　　　　  　　　 …………2分

　　　 ∵当３＜x≤5即–1<x–4≤1时，依已知可得：

　　　 f(x)=f(x-4)=(x-4)²+2(x-4)=x²-6x+8　　 (3<x≤5)　　　　　　  …………2分

 （Ⅱ）函数f(x)在（３，５]上是增函数.　 　　　　　　　　　　　　　…………６分

　　　 证明如下：任取x₁,x₂使得3<x₁<x₂≤5　　　　　　　　　　　　　 …………7分

　　　 f(x₁)-f(x₂)=x₁²-6x₁+8-x₂²+6x₂-8=(x₁-x₂)(x₁+x₁-6)<0　　　 　　　　…………9分

　　　 这是因为：x₁­–x₂<0,且依3<x₁<x₂≤5可知：x₁+x₂-6>0

　　　 可推得：f(x₁)<f(x₂)因此，函数f(x)在（3,5]上是增函数.　　　 …………10分　　　　

（21）本题满分14分

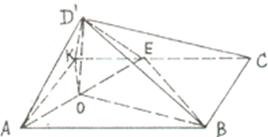
（Ⅰ）解：∵二面角Ｄ'­－AE­－B是直二面角，

　　　　  ∴平面Ｄ'AE⊥平面ABCE　　　　　　　　　　　　　　　　

　　　　　  作Ｄ'O⊥AE于O,连结OB

　　　　∴Ｄ'O⊥平面ABCE

　　　　

　　　　∴ ∠Ｄ'BO是直线Ｄ'B与平面ABCE所成的角.　　　　　　　　  …………2分　　

　　　　∵Ｄ'A=Ｄ'E=a,且Ｄ'O⊥AE于O,∠AＤ'E=90°

　　　 ∴O是AE的中点,

　　　　 AO=OE=D'O=

　　　　在△OAB中,OB=

　　　　　　　　　  =

　　　　在直角△D'OB中,tg(∠D'BO)=.　　　 　　　………理4分,文5分　　

　　　　（Ⅱ）证明：如图，连结BE,

　　　　　　  ∵∠AED=∠BEC=45°,

　　　　　　  ∴∠BEA=90°

　　　　　 即BE⊥AE于E　　　　　　　　　　　　　　　　　  ………理6分,文8分

　　　　　　 ∵D'O⊥平面ABCE,

　　　　　　 ∴D'O⊥BE,

　　　　　　 ∴BE⊥平面AD'E,　　　　　　　　 

　　　　　　　 BE⊥AD　　　　　　　　　　　　　　　　　　  ………理8分,文10分

（Ⅲ）解,四边形ABCE是直角梯形

　　　

　　

　　　　　　　　　　　………理10分,文14分

（Ⅳ）作AK∥BC交CE的延长线于K,

∴∠D'AK是异面直线AD'与BC所成的角.　　　　　　　　　　　　  ………理11分

∵四边形ABCK是矩形

∴AK=BC=EK=a.　　　　　　　　　　　　　　　　　　　　　　　　 ………理12分

连结OK,D'K,

∴OK=D'O=

△D'AK是正三角形　 ∴∠D'AK=60°

即异面直线AD'与BC成60°角. 　　　　　　　　　　　　　　　　　………理14分

（22）本题满分12分

（Ⅰ）解： 　　　　　　　　　　　　　　　　　 ………2分

　　 　………４分

　　　 　　　　　　　　　　　　　　　　　　　　………６分

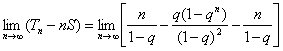（Ⅱ）　　　　　　　　  ………８分

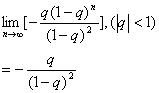　　 　　　　　　　　　　　　　　　　　　………12分

（23）本题满分12分

（Ⅰ）解：m=kv²

　　　　 t=f(v)=　　　　　　　　　　　　　　　　  ………3分

　　　  (0<v≤v₀)　　　　　　　　　　　　　　　　　　　　　　 　 ………4分

（Ⅱ）解：

　　　　 仅当时上式中等号成立　　　　　  ………６分

（１）当时，t取得值最小值，其最小值为：

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  ………８分

（２）当

　　　　

　　　　　　　　　　 　　　　　　　　　　 ………10分

　　　　

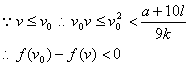
因此,当v=v₀时,t有最小值,其最小值为

　　　　　　　　　　　　　　　　　　　　　　　　　　　 ………12分

（24）本题满分14分

（Ⅰ）解：由(x–3)²+y²=9-a(a<9)可知圆心

　　　 Ｍ的坐标为（3,0）　　　………２分

　　　 依题意：

　　　

　　　MA,MB的斜率k满足: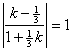　　　　　　　　　　

　　　　　　　　　　　　  ………4分

解得:k_AC=　　  ………6分

（Ⅱ）理科作：设MB、MA的倾斜角分别为

　　　可以推出:

　　　再设

　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　　　　　　 ………9分

　设抛物线方程为y²=2px(p>0),由于A,B两点在抛物线上,

　

　 　　　　　　　　　　　　　　　　　　 

得抛物线方程为y²=x　　　　　　　　　　　　　  ………12分

　　可知Ａ点坐标为(1,1)，且Ａ点关于Ｍ(3,0)的对称点Ｃ的坐标是（5,–1）

直线l的方程为

　　　　　 即x–3y­–8=0　　　　　　　　　　　　　　　　　  ………14分

文科作：解：将圆方程分别与AC、BD直线方程：

　　联立，可解得Ａ(–1,2),B(5,4)　　　　 ………9分

　　设抛物线方程为y²=a(x–m)　 (*)　　　　　　　　　　　　　　　　  ………10分

将A(–1,2)、B(5,4)的坐标代入(*),得

　4=a(–1–m)

　　　　　　　 解得:a=2,m=­–3

　16=a(5–m)

　　∴抛物线的方程为y²=2(x+3)　　　　　　　　　　　　　　　　　　 ………12分

A(–1,2)点关于Ｍ(3,0)点的对称点为Ｃ（7,–2）

故直线l的方程为

　　　　　　  即x­–3y–13=0　　　　　　　　　　　　　　　　　　　  ………14分

说明：囿于篇幅本答案只给出一种解法，在评卷过程中若有不同的作法，请按相应步骤评分.