高三数学第三次质量检测试题
说明：本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共150分.考试时间120分钟.第Ⅰ卷 (选择题 共60分)
一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）
1.设f(x)=
＋arctgx,f(x)的反函数是f－1(x),则f－1(
)等于
A.－
B.－
C. D.
2.在正方体ABCD—A1B1C1D1中，E、F分别为D1C1、CC1的中点，则直线EF与BD所成的角为
A.90° B.６０° C.45° D.３０°
3.不等式
>x＋1的解集为
A.{x－2<x<2} B.{x－1≤x<2} C.{x－
≤x<－1} D.{x－≤x<2}
4.50名乒乓球单打选手进行淘汰赛（胜者进入下一轮，败者淘汰出局），直至争出冠军，则
共比赛
A.47场 B.48场 C.49场 D.50场
5.(理)圆ρ=－sinθ的圆心的一个极坐标是
A.（1，） B.（1，
） C.（
，） D.( ，)
（文）过点A（1，1）、B（－1，－1）且圆心在直线x－y－2=0上的圆的方程是
A.（x－3）2＋(y－1)2=4 B.(x＋3)2＋(y＋1)2=4
C.(x＋1)2＋(y－1)2=4 D.(x－1)2＋(y＋1)2=4
6.设a=cos6°－
sin6°,b=
, ,则有
A.a>b>c B.a<b<c C.a<c<b D.b<c<a
7.若双曲线的虚轴长为8，两顶点A（2，1）和A′(2,－5)，则其离心率是
A.
B. 
C.
D.
8.等差数列{an}的首项a1=－5，它的前11项的算术平均数为5，若从中抽去一项，余下各项
的算术平均数为4，则抽去的一项是
A.a7 B.a8 C.a9 D.a11
9.把一个面积为3π,顶角为120°的扇形卷成一个圆锥，则该圆锥的体积等于
A.
B.
C.
D.
10.为了使函数y=sinωx(ω>0)在区间［0，1］上至少出现50次最大值，则ω的最小值是
A.98π
B.
C. 
D.100π
11.设圆（x－3)2＋(y＋5)2=r2上有且仅有两个点到直线4x－3y=2的距离等于1，则圆半径r的取值范围是
A.4<r<6 B.4≤r＜6
C.4<r≤6
D.4≤r≤6
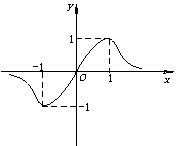
12.设函数f(x)=
的图象如图所示，则a、b、c的大小关系是
A.a>b>c B.a>c>b
C.b>a>c D.c>a>b
第Ⅱ卷 (非选择题 共90分)
二、填空题（本大题共4小题，每小题4分，共16分.把答案填在题中横线上）
13.一个球从100米高处自由落下，每次着地后又跳回到原高度的一半再落下，当它最后静止在地面上时，共经过了___________米.
14.以一个三棱柱的顶点为顶点的棱锥共有___________个.
15.椭圆
=1的两个焦点为F1、F2，点P在椭圆上，若PF1⊥PF2，则点P到x轴的距离为___________.
16.有以下四个命题：
①2n>2n＋1(n≥3)
②2＋4＋6＋……＋2n=n2＋n＋2(n≥1)
③凸n边形内角和为f(n)=(n－1)π(n≥3)
④凸n边形对角线的条数f(n)=
(n≥4)
其中满足“假设n=k（k∈N*，k≥n0)时命题成立，则当n=k＋1时命题也成立.”但不满足“当n=n0(n0是题中给定的n的初始值）时命题成立”的命题序号是_________.
三、解答题（本大题共6个小题，共74分.解答应写出文字说明、证明过程或演算步骤）
17.（本小题满分12分）
已知复数z1=［
］2,设z1在复平面上对应点A，如果点A、B及坐标原点O构成以OB为斜边的直角三角形，且∠AOB=30°,求点B对应的复数z2.
18.（本小题满分12分）
(理)过抛物线y=x2上定点C（1，1）引两条互相垂直的弦CA、CB，作CM⊥AB，M为垂足，求点M的轨迹方程.
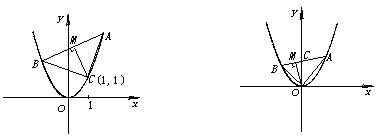（文）过抛物线y=x2的顶点引两条互相垂直的弦OA、OB，作OM⊥AB，M为垂足，求点M的轨迹方程.
19.（本小题满分12分）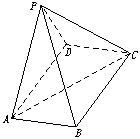
如图，四棱锥P—ABCD的底面是矩形，侧面PAD是正三角形，且侧面PAD⊥底面ABCD.
（Ⅰ）求平面PAB与平面PCD所成二面角的大小；
（Ⅱ）当
的值等于多少时，能使PB⊥AC？请给出证明.
20.（本小题满分12分）
（理）已知{an}是等比数列，Sn为它的前n项和，且Sn＋an=4.
(Ⅰ)求Sn;
(Ⅱ)是否存在正整数c和k，使
>2成立？
（文）已知{an}是等比数列，Sn为它的前n项和，且Sn＋an=4.
(Ⅰ)求Sn;
(Ⅱ)是否存在正整数k,使
>2成立？
21.(本小题满分12分)
已知水渠在过水断面面积为定值的情况下，过水湿周越小，其流量越大.
现有以下两种设计，如图甲、图乙.
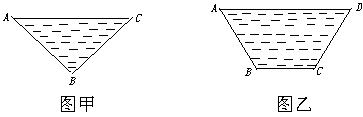
图甲的过水断面为等腰△ABC，AB=BC，过水湿周l1=AB＋BC
图乙的过水断面为等腰梯形ABCD，AB=CD，AD∥BC，∠BAD=60°,过水湿周l2=AB＋BC＋CD,若△ABC与梯形ABCD的面积都是S.
（Ⅰ）分别求l1和l2的最小值；
（Ⅱ）为使流量最大，给出最佳设计方案.
22.（本小题满分14分）
（理）已知函数f(x)在（－1，1）上有定义，f()=－1,当且仅当0<x<1时，f(x)<0,且对任意x、y∈(－1,1),都有f(x)＋f(y)=f(
).试证明：
（Ⅰ）f(x)为奇函数；
（Ⅱ）f(x)在（－1，1）上单调递减；
（Ⅲ）1＋f(
)＋f(
)＋…＋f(
=0.(n∈N*)
（文）已知函数f(x)在（－1，1）上有定义，f()=－1，当且仅当0<x<1时，f(x)<0,且对任意x、y∈(－1,1),都有f(x)＋f(y)=f（）.试证明：
（Ⅰ）f(0)=0且f(x)为奇函数；
（Ⅱ）若对数列{xn}满足：x1=,xn＋1=
,求f(xn);
(Ⅲ)在（Ⅱ）的条件下，求
.
高三数学第三次质量检测试题答案
一、1.A 2.B 3.D 4.C 5.D 6.C 7.B 8.D 9.A 10.B 11.A 12.B
二、13. 300 14. 18 15. 4 16.②③
三、17.解：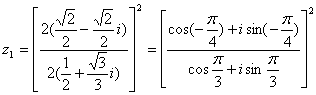
2分
4分
=
6分
∵Rt△OAB中，∠AOB=30°
∴点B对应的复数
8分
∴
12分
注：①
可用代数式直接计算；
②
可据图形，由平面几何、三角知识计算.
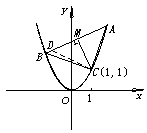18.(理)解：设
则直线AB方程为：
2分
即
4分
∵CA⊥CB，
即m＋n＋mn=－2 6分
故直线AB方程为：y=(m＋n)x＋m＋n＋2 8分
即y=(m＋n)(x＋1)＋2
∴直线AB过定点D(－1，2)，又CM⊥AB
∴点M在以CD为直径的圆上 10分
其方程为：
12分
注：①由于点C是点M的极限点，是否除去该点，评分时不予考虑；
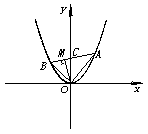②可引进AC斜率k为参数；
③求轨迹可用交轨法.
(文)解：设点
,则直线AB方程为：
2分
即
4分
又OA⊥OB，∴
6分
∴直线AB方程为：
8分
即直线AB过定点C(0，1)
∵OM⊥AB，∴点M在以OC为直径的圆上 10分
∴点M方程为：
即：
12分
注：①由于原点O是点M的极限点，是否除去点O，评分时不予考虑；
②可引进OA斜率k为参数；
③求轨迹可用交轨法.
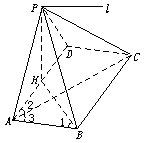19.解：(Ⅰ)设平面PAB∩平面PCD=l
∵AB∥CD ∴AB∥面PCD
∴AB∥l CD∥l 2分
∵平面PAD⊥底面ABCD，且AB⊥AD
∴AB⊥面PAD
∴AB⊥PA，AB⊥PD 4分
∴l⊥PA,l⊥PD
∴∠APD为二面角AB—l—CD的平面角
∵△PAD为正三角形 ∴∠APD=60° 6分
(Ⅱ)当
时，PB⊥AC
7分
取AD中点H，连PH、HB，则PH⊥AD
∵侧面PAD⊥底面ABCD
∴PH⊥底面ABCD 9分
在Rt△HAB中，tg
在Rt△ADC中，tg
∴∠1=∠2 又∠2＋∠3=90°
∴∠1＋∠3=90° ∴HB⊥AC 11分
故PB⊥AC
注：①若作l∥AB,必须证明l是平面PAB与平面PCD的交线；
②由于是PB⊥AC的充要条件，第(2)问可用逆推法.
20.(理)解：(Ⅰ)由于
,令n=1,2.得
,因为{an}是等比数列
∴q=
2分
∴
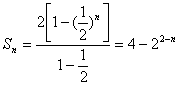4分
(Ⅱ)假设存在正整数c、k使不等式成立，即
6分
8分
10分
∵c、k是正整数，∴
是整数，与上式矛盾
故不存在正整数c、k使不等式成立. 12分
注：第(2)问推理方式较多，视情况酌情给分.
(文)解：(Ⅰ)(同理)
4分
(Ⅱ)
6分
8分
10分
∵k是正整数，2k－1也是正整数.
故不存在正整数k使不等式成立. 12分
21.解：(Ⅰ)在图甲中，设∠ABC=θ,AB=BC=a,则
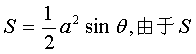、a、sin
皆为正值，可解得：
≥
3分
当且仅当sinθ=1,即θ=90°时取等号
∴
≥2
在图乙中，设
可求得：
由
5分
∴
≥
8分
当且仅当
时取等号
10分
(Ⅱ)由于
,则l2的最小值小于l1的最小值
11分
故在方案②中当l2取得最小值时的设计方案(
)为最佳方案
12分
22.(理)证明：(Ⅰ)由
得
∴
1分
令
即
∴f(x)为奇函数 3分
(Ⅱ)先证在(0，1)上f(x)单调递减.
令
.
4分
∵ ∴
∴
又
5分
∴
∴0<
<1 6分
由题设条件知
（）<0
即
故在(0，1)上f(x)单调递减成立 7分
又由f(x)为奇函数，可知f(x)在(－1，1)上单调递减. 8分
(Ⅲ)由题设条件可得
∴
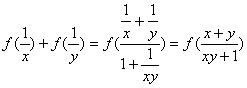
11分
∴
12分
13分
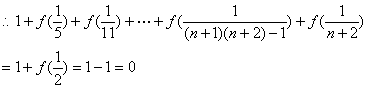14分
(文)证明：(Ⅰ)由
∴
∴f(0)=0
2分
即 ∴f(x)为奇函数
6分
(Ⅱ)∵
8分
∴
10分
∴
为首项，2为公比的等比数列
∴
11分
(Ⅲ)由(2)知
∴
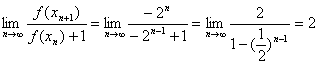14分