高三数学第四次月考试卷
第I卷
一、选择题(每小题5分,共60分)
1. 在直角坐标系中,面积为8的Δ![]() 在映射
在映射![]() 的作用下的象集为Δ
的作用下的象集为Δ![]() ,则Δ
,则Δ![]() 的面积等于
( )
的面积等于
( )
(A)9
(B)![]() (C)6
(C)6![]() (D)8
(D)8
2. 已知A(-1, 0), B(1, 0),动点P满足PA+PB=2,则点P的轨迹方程是 ( )
(A)x2+y2=1 (B)y=0
(C)y=0, x∈[-1, 1]
(D)![]()
3. 函数![]() 图象的一条对称轴方程是
图象的一条对称轴方程是![]() ,则直线
,则直线![]() 的倾斜角为
的倾斜角为
(A) ![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]() ( )
( )
4. 设D点在曲线![]() (
(![]() 为参数)上,D点到直线4x-3y-2=0的距离为d,则d的范围为
为参数)上,D点到直线4x-3y-2=0的距离为d,则d的范围为
(A)[0,1] (B)[1,2] (C)[0,2] (D)[1,3] ( )
5. 抛物线y2=2px与直线ax+y-4=0交于两点A、B,其中点A的坐标是(1,2).设抛物线的焦点为F,则FA+FB等于 ( )
A.7 B.![]() C.6 D.5
C.6 D.5
6. 若双曲线的一个顶点到两条准线的距离和等于4,一个焦点到两条渐近线的距离和等于8,则双曲线的离心率是 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
7.设椭圆ax2+by2=1的焦点在y轴上,且a,b∈{1,2,3,4,5,6},则这样的椭圆共有 ( )
A.![]() B.
B. ![]() -6 C.
-6 C.![]() D.
D. ![]()
8.已知双曲线中心在原点且一个焦点为F(![]() ,0),直线y=x-1与其相交于A,B两点,AB中点的横坐标为-2,则此双曲线的方程是
( )
,0),直线y=x-1与其相交于A,B两点,AB中点的横坐标为-2,则此双曲线的方程是
( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
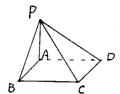 9. 过正方形ABCD的顶点A,引PA⊥平面ABCD,
9. 过正方形ABCD的顶点A,引PA⊥平面ABCD,
若PA=AB,则面ABP和面CDP所成的二面角
的大小是( )
A.30° B.45°
C.60° D.90°
10. 已知直二面角![]() ,直线
,直线![]() ,直线
,直线![]() ,且
,且![]() 与
与![]() 不垂直,
不垂直,![]() 与
与![]() 不垂直,那么( )
不垂直,那么( )
A.![]() 与
与![]() 可能垂直,但不可能平行
B.
可能垂直,但不可能平行
B.![]() 与
与![]() 可能垂直,也可能平行
可能垂直,也可能平行
C.![]() 与
与![]() 不可能垂直,不可能平行
D.
不可能垂直,不可能平行
D.![]() 与
与![]() 不可能垂直,但可能平行
不可能垂直,但可能平行
11. 已知相交直线l、m都在平面α内,并且都不在平面β内,若p:l、m中至少有一条与β相交;q:α与β相交;则p是q的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.不充分也不必要条件
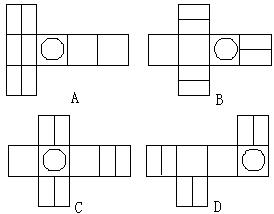
12. 正方体的直观图如右图所示,则其展开图是 ( )

二、填空题(每小题4分,共16分)
13.若直线![]() 与抛物线
与抛物线![]() 的两个交点都在第二象限,则
的两个交点都在第二象限,则![]() 的取值范围是
.
的取值范围是
.
14.如果正△ABC中,D∈AB,E∈AC,向量![]() ,那么以B,C为焦点且过点D,E的双曲线的离心率是
.
,那么以B,C为焦点且过点D,E的双曲线的离心率是
.
15.将抛物线x2=2y按向量a=(-3,2)平移后恰与直线2x-y+6=0相切,则切点坐标为__________.
16. 如果三棱锥的三个侧面两两垂直,它们的面积分别为6cm2、4cm2和3cm2,那么它的外接球表面积是 。
三、解答题
17. (本小题满分12分)
已知过点P的直线l绕点P按逆时针方向旋转![]() 角﹝0<
角﹝0<![]() <
<![]() =,得直线为x-y-2 = 0,若继续按逆时针方向旋转
=,得直线为x-y-2 = 0,若继续按逆时针方向旋转
![]() -
-![]() 角,得直线2x+y-1 = 0,求直线l的方程。
角,得直线2x+y-1 = 0,求直线l的方程。
18.(本小题12分)
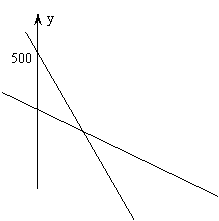
某厂准备生产甲、乙两种适销产品,每件销售收入分别为3千元,2千元.甲、乙产品都需要在A,B两种设备上加工,在每台A,B上加工一件甲产品所需工时分别为1时、2时,加工一件乙产品所需工时分别为2时、1时,A,B两种设备每月有效使用台时数分别为400和500.如何安排生产可使收入最大?
![]()
![]() y
y
![]()
![]() O
x
O
x
19. (本小题12分)
坐标平面内有三点A(-1,0),B(1,0),P(x , y),若满足![]() =a,
=a,![]() =b,且a·b=2.求
=b,且a·b=2.求
(I) 点P的轨迹方程;
(II)
求![]() 与
与![]() 的夹角θ的最大值.
的夹角θ的最大值.
20. (本小题12分)
在底面为等腰直角三角形的直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=A1A.
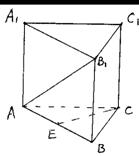 (I) 求AB1与BC1所成的角;
(I) 求AB1与BC1所成的角;
(II) 若点E为AB的中点,求CE与BC1所成的角;
(III) 求二面角A1-AB1-C1的大小.
21.(本小题12分)
坐标平面内,O为原点,A(4,-3)为⊿OAB的直角顶点.已知![]() ,且点B的纵坐标大于零.
,且点B的纵坐标大于零.
(1)
求向量![]() 的坐标;
的坐标;
(2) 求圆x2-6x+y2+2y=0关于直线OB对称的圆的方程;
(3) 若抛物线y=ax2-1上总有关于直线OB对称的两个点,求a的取值范围.
22.(本小题14分)
已知常数a>0,向量![]() .以
.以![]() 为方向向量且过原点O的直线记作l1,以
为方向向量且过原点O的直线记作l1,以![]() 为方向向量且过定点A(a,0)的直线记作l2,
为方向向量且过定点A(a,0)的直线记作l2,![]() R, l1与l2相交于点P,试问:是否存在两个位于x轴上的定点E,F,使得
R, l1与l2相交于点P,试问:是否存在两个位于x轴上的定点E,F,使得![]() 为定值?若存在,求出E,F的坐标;若不存在,说明理由.
为定值?若存在,求出E,F的坐标;若不存在,说明理由.
高三数学第四次月考试卷参考答案与评分意见
一、选择题
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| D | C | A | C | A | C | C | C | B | D | C | D |
二、填空题
13.(-3,0) 14.![]() +1
15.(-1,4) 16.29π
+1
15.(-1,4) 16.29π
三、解答题
17. 解:如图,直线l与直线2x+y-1=0垂直,
且P点就是已知两直线的交点 ……4分
由![]() 得
得![]() ∴P(1,-1)
……8分
∴P(1,-1)
……8分
∴直线l的方程为y+1=(x-1),
即x-2y-3=0. ……12分
18. 解: 设甲、乙两种产品的产量分别为x,y件,约束条件是
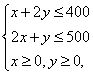
目标函数是![]() ,要求出适当的x,y,
,要求出适当的x,y,
使![]() 取得最大值。
……6分
取得最大值。
……6分
作出可行域,如图
![]()
|
 |
设![]() 是参数,将它变形为
是参数,将它变形为![]() ,这是斜率为
,这是斜率为![]() ,随a变化的一族直线。当直线与可行域相交且截距
,随a变化的一族直线。当直线与可行域相交且截距![]() 最大时,目标函数f取得最大值。
………8分
最大时,目标函数f取得最大值。
………8分
由![]() 得
得![]() ,……………………10分
,……………………10分
因此,甲、乙两种产品的每月产品分别为200,100件时,可得最大收入800千元.…12分
19.解(I)由条件a =![]() =(-1-x,-y),b=
=(-1-x,-y),b=![]() =(1-x,-y),
……2分
=(1-x,-y),
……2分
∵ a·b=2,∴(-1-x) (1-x)+(-y)2=2 ……4分
整理得x2+y2=3即为所求的轨迹方程. ………6分
(II)在⊿ABP中,∠APB=θ,
由余弦定理得AB2=a2+b2-2abcosθ=a2+b2-2 a·b
∴a2+b2=8(定值) ………8分
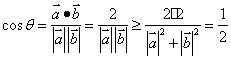 ………10分
………10分
∵0≤θ≤π∴0≤θ≤即θ的最大值为 ……12分
20. 解:(1)方法一:连结B1C交BC1于O,取AC中点D,连结OD可得∠BOD=90°,
AB1与BC1成90°角.
方法二:AB1在面BB1C1C上的射影是B1C,与BC1垂直,由三垂线定理得证.
 方法三:补体成正方体亦可获证.
……4分
方法三:补体成正方体亦可获证.
……4分
(2)取A1B1中点F,连结C1F、BF,可得∠BC1F=60°,
CE与BC1所成角60°. ……8分
(3)在平面A1B中作FH⊥AB1于H,连结C、H,
可证∠C1HF为二面角的平面角,
∠C1HF=60°. ……12分
21.解:(1)设![]() =(u,v),则由
=(u,v),则由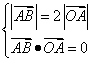 得
得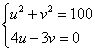
解之得![]() ………………2分
………………2分
![]() ,且点B的纵坐标
,且点B的纵坐标![]() >0,∴
>0,∴![]()
因此![]() =(6,8).
…………4分
=(6,8).
…………4分
(2)由(1)知![]() =(10,5),∴直线OB的方程为y=x. ……………………5分
=(10,5),∴直线OB的方程为y=x. ……………………5分
已知圆的标准方程为(x-3)2+(y+1)2=10,圆心(3,-1)关于直线OB的对称点为(a,b),则
由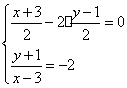 解得
解得![]()
故所求圆的方程为(x-1)2+(y-3)2=10 ……………7分
(3)设P(x1,y1),Q(x2, y2)为抛物线y=ax2-1上关于直线OB对称的两点,则
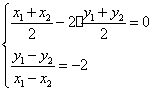
即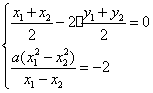 ……………8分
……………8分
得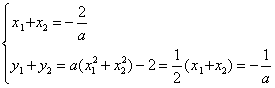
所以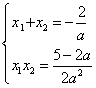 ……10分
……10分
x1,x2是方程x2+![]() x+
x+![]() =0的两个相异实根,于是
=0的两个相异实根,于是
Δ=![]() 解得a>. ……………12分
解得a>. ……………12分
22.解:∵![]() ∴
∴![]() =(a,λ),
=(a,λ),![]() =(-2λa,1)……2分
=(-2λa,1)……2分
因此直线l1的方程是ay=λx,l2的方程是-2λay=1·(x-a). ……4分
消去参数λ,得点P(x,y)满足方程x2+2ay2-ax=0, ……6分
整理得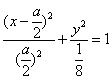 ①
……8分
①
……8分
∵a>0,所以有
(ⅰ)当![]() 时,方程①表示圆的方程,故不存在合乎题意的定点E,F;
时,方程①表示圆的方程,故不存在合乎题意的定点E,F;
(ⅱ)当a> ![]() 时,方程①表示椭圆,E(
时,方程①表示椭圆,E(![]() ,0),F(
,0),F(![]() ,0)为两个焦点,故E,F是合乎题意的两个定点;
,0)为两个焦点,故E,F是合乎题意的两个定点;
(ⅲ)当0<a<![]() 时,方程①也表示椭圆,但焦点在直线x=
时,方程①也表示椭圆,但焦点在直线x=![]() 上,不合乎题意. ……14分
上,不合乎题意. ……14分
(以上三种情况各2分)