高考能力测试步步高数学基础训练33
基础训练33(A) 平面与平面的平行和垂直
●训练指要
掌握平面与平面的位置关系特征，能根据判定定理性质定理证明有关平行与垂直问题.
一、选择题
1.下列命题中，正确的是
A.如果一个平面内的两条直线与另一个平面平行，则这两个平面平行
B.如果一个平面内的无数条直线与另一个平面平行，则这两个平面平行
C.如果一个平面内的两条直线分别与另一个平面内的两条直线平行，则这两个平面平行
D.如果一个平面内的两条相交直线分别与另一个平面内的两条直线平行，则这两个平面平行
2.给出下列四个命题：
①平行于同一条直线的两个平面平行；
②垂直于同一条直线的两个平面平行；
③平行于同一平面的两个平面平行；
④垂直于同一平面的两个平面平行.
其中真命题的个数是
A.1 B.2 C.3 D.4
3.对于直线m、n和平面α、β，α⊥β的一个充分条件是
A.m⊥n,m∥α,n∥β B.m⊥n,α∩β=m,n
α
C.m∥n,n⊥β,mα D.m∥n,m⊥α,n⊥β
二、填空题
4.如果平面α内的一条直线垂直于平面β内的两条相交直线，则平面α和β_________.
5.在空间两两垂直的平面最多有_________个.
三、解答题
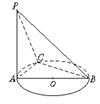
6.如图，AB是⊙O的直径，PA垂直于⊙O所在的平面，C是圆周上不同于A、B的任意一点.求证：平面PAC⊥平面PBC.
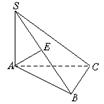7.如图，已知S为△ABC所在平面外一点，SA⊥平面ABC，平面SAB⊥平面SBC.
求证：AB⊥BC.
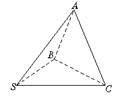8.如图，已知∠BSC=90°,∠BSA=∠CSA=60°,又SA=AB=AC，求证：平面ABC⊥平面SBC.
基础训练33(B) 空间向量及其运算
●训练指要
理解空间向量及其有关的概念.掌握向量的表示法、向量的加法、减法、数乘、数量等运算方法和性质，熟练地进行有关运算.
一、选择题
1.(2002·上海)若a、b、c为任意向量，m∈R,则下列等式不一定成立的是
A.(a+b)+c=a+(b+c) B.(a+b)·c=a·c+b·c
C.m(a+b)=ma+mb D.(a·b)c=a(b·c)
2.设有三个空间向量a、b、c，已知a与b不平行，λ、μ是两个实数，则a、b、c三个向量共面是c=λa+μb的
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分又非必要条件
3.(2001年上海)如图，在平行六面体ABCD—A1B1C1D1中，M为AC与BD的交点，若
=a，若
=b,若
=c，则下列向量中与
相等的向量是
A.-
a+b+c B.a+b+c
C.a-b+c D.-a-b+c
二、填空题
4.已知A、B、C、D为空间四点，此四点共面的一个充分必要条件是_________.(用向量表示)
5.已知a+3b与7a-5b垂直，且a-4b与7a-2b垂直，则<a,b>=_________.
三、解答题
6.求与a=(2，-1，2)共线且满足a·z=-18的向量z.
7.证明四点A(1，0，1)，B(4，4，6)，C(2，2，3)，D(10，14，17)在同一平面上.
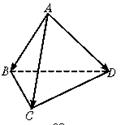
8.在四面体ABCD中，已知AB⊥CD，AC⊥BD，求证：AD⊥BC.
高考能力测试步步高数学基础训练33答案
基础训练33(A) 平面与平面的平行和垂直参 考 答 案
一、1.D 2.B 3.C
二、4.重直 5.3
三、6.
7.略
8.A在面SBC上的射影为△SBC的外心即△SBC的斜边的中点D，∴AD⊥面SBC，面ADABC，故面ABC⊥面SBC
基础训练33(B) 空间向量及其运算参 考 答 案
一、1.D 2.C 3.A
二、4.存在实数x、y,使得
;(或存在实x,y，对空间任一点O，
;或存在实数x、y、z,对空间任一点O，
(x+y+z=1)); 5.60°
三、6.设z=λa则z=(2λ，－λ，2λ)
因为a·z=－18
所以4λ+λ+4λ=－18,所以λ=－2
所以z=(－4，2，－4)
7.
若设
则(9,14,16)=(3x+y,4x+2y,5x+2y)
所以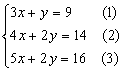
由(1)(2)得
把它代入(3)也成立
所以
所以A、B、C、D四点共面
8.设
=a，
=b，
=c,
则
=b－a,
=c－b,
=c－a.∵AB⊥CD,
∴
=0，
即a·(c－b)=0，∴a·c=a·b
又AC⊥BD，∴
=0，即b·(c－a)=0,∴b·c=b·a，
∴
=c·(b－a)=c·b－c·a=b·a－a·b=0，
∴AD⊥BC.