等差与等比数列综合能力测试题

高考真题选讲

等差与等比数列综合能力测试题

　

(一)选择题

1．在数列{a_n}中，a_n=qⁿ(q≠0)，则下列结论不恒正确的是[　  ]

2．设{a_n}为等比数列，{b_n}为等差数列，且b₁=0，c_n=a_n+b_n，若数列{c_n}是1，1，2，…，则{c_n}的前10项之和是[　　]

A．978 B．557C．467 D．非上述答案

3．若A是a，b(a，b∈R⁺)的等差中项，G＞0且是a，b的等比中项，则[　  ]

A．ab≥A·G B．ab≤A·G

C．ab＞A·G D．ab＜A·G

(二)填空题

1．若{a_n}(a_n＞0)成等比数列且a₁a₁₀₀=64，则log₂a₁+log₂a₂+…+log₂a₁₀₀=______．

2．若a，b，c成等差数列，同时又成等比数列，则a，b，c间的关系为______．

3．设α，β，γ成等差数列，其公差为π的整数倍，则sinα，sinβ，sinγ成______数列．

4．有四个数，前三个数成等比数列，其积为216，后三个数成等差数列，其和为12，则此四数是______．

(三)解答题

(1)求证该数列是等比数列；

(2)当b为何值时，这个数列既是等比数列又是等差数列．

2．已知sin2x和sinx分别是sinθ和cosθ的等差中项和等比中项，求cos2x．

3．已知等比数列a₁，a₂，…及等差数列b₁，b₂，…满足不等式

4．若a，b，c同时是一个等比数列和一个等差数列的第k，m，n项，求证　a^b-cb^c-ac^a-b=1．

5．在数列{a_n}中，前n项和S_n=an²+bn，其中a＞0，a+b＞1，

数列．

6．设{a_n}是等比数列，公比为q＞0，q≠1，若A=a₁+a₂+…+a_n，

参考答案　

(一)选择题  1．C　2．A　3．B

(二)填空题  1．300；

2．a=b=c．

3．①当α=nπ(n∈Z)时成等差数列

②当α≠nπ(n∈Z)设公差d=kπ

i)若k为奇数，则sinα，sinβ，sinγ成公比为-1的等比数列

ii)若k为偶数，则sinα=sinβ=sinγ≠0，此时既是等比数列，又是等差数列；

4．9，6，4，2．

(三)解答题

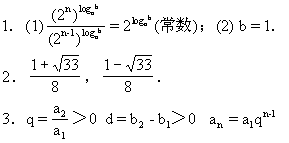
b_n=b₁+(n-1)·d

∴log_aa_n-b_n=log_aa₁+(n-1)·log_aq-b₁-(n-1)·d

=(log_aa₁-b₁)+(n-1)·(log_aq-d)　依题意

4．设等差数列的首项为a₁，公差为d，等比数列首项是b₁，公比为q

则　　　　　　　　　　　 a=b₁·q^k-1，b=b₁·q^m-1，c=b₁·q^n-1

b-c=(m-n)·d　c-a=(n-k)·d  a-b=(k-m)·d

代入左边即证．

5．可求得{a_n}是以a+b为首项，公差为2a的等差数列．

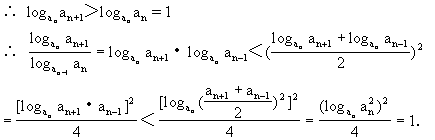
∴是递减数列．

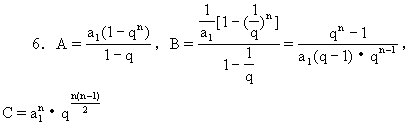
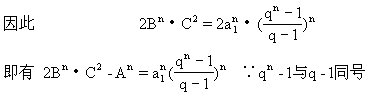
综上可得

当a₁＞0时2BⁿC²＞Aⁿ

当a₁＜0时　n为偶数时　2BⁿC²＞Aⁿ

n为奇数时　2BⁿC²＜Aⁿ．