第一学期高三数学期中试卷
第I卷(选择题,共60分)
一. 选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 若![]() 的定义域为M,
的定义域为M,![]() 的定义域为N,令全集
的定义域为N,令全集![]() ,则
,则![]() ( )
( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
2. 已知数列![]() 中,
中,![]() ,则这个数列前n项和的极限是( )
,则这个数列前n项和的极限是( )
A. 2 B.
![]() C.
3 D.
C.
3 D.
![]()
3. 已知函数![]() ,则它的反函数
,则它的反函数![]() 的图像是( )
的图像是( )
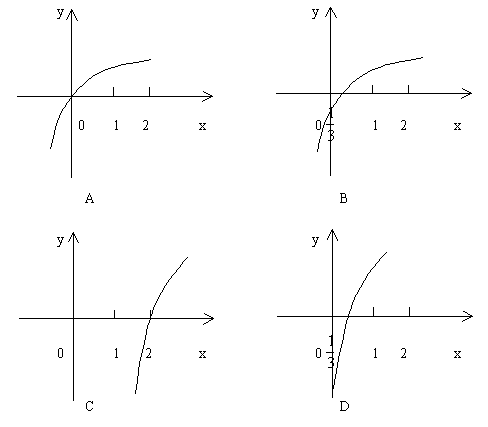
4. 如图,圆柱的高为8,点A和点B分别在上下底面的圆周上,且![]() ,则直线AB与圆柱的轴
,则直线AB与圆柱的轴![]() 所成角的大小为( )
所成角的大小为( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
5. 函数![]() 图像的两条相邻对称轴之间的距离是( )
图像的两条相邻对称轴之间的距离是( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
6. (理科作)过点![]() 且平行于极轴的直线的极坐标方程是( )
且平行于极轴的直线的极坐标方程是( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
7. (文科作)点![]() 关于直线
关于直线![]() 对称的点的坐标是( )
对称的点的坐标是( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
8. 圆台的侧面展开图是一个内外半径分别为3和6,中心角为![]() 的扇环,则此圆台的全面积是( )
的扇环,则此圆台的全面积是( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
9. 定义在![]() 上的函数
上的函数![]() 在
在![]() 上是增函数,且函数
上是增函数,且函数![]() 图像的对称轴是
图像的对称轴是![]() ,则( )
,则( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
10. 若圆![]() 上有且仅有两个点到直线
上有且仅有两个点到直线![]() 的距离等于1,则半径R的取值范围是( )
的距离等于1,则半径R的取值范围是( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
11. 某体育彩票规定:从01至36共36个号中抽出7个号为一注,每注2元。某人想从01至10中选3个连续的号,从11至20中选2个连续的号,从21至30中选1个号,从31至36中选1个号组成一注,则这人把这种特殊要求的号买全,至少要花( )
A. 3360元 B. 6720元 C. 4320元 D. 8640元
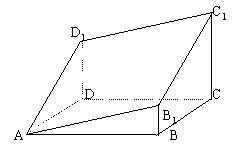
12. 图中多面体是过正四棱柱的底面正方形ABCD的点A作截面AB1C1D1而截得的,且B1B=D1D。已知截面AB1C1D1与底面ABCD成![]() 的二面角,
的二面角,![]() ,则这个多面体的体积为( )
,则这个多面体的体积为( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
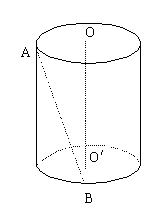
13. 已知双曲线![]() 的离心率
的离心率![]() ,令双曲线两条渐近线构成的角中,以实轴为角平分线的角为
,令双曲线两条渐近线构成的角中,以实轴为角平分线的角为![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
第II卷(非选择题共90分)
二. 填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上。
14. 若![]() 展开式中的第5项为常数,则
展开式中的第5项为常数,则![]() 。
。
15. 抛物线![]() 的准线方程是
。
的准线方程是
。
16. 已知![]() ,则
,则![]() 是值是
。
是值是
。
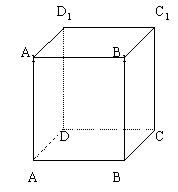
17. 已知如图,正方体ABCD—A1B1C1D1,过点A作截面,使正方体的12条棱所在直线与截面所成的角皆相等,试写出满足这样条件的一个截面 。(注:只需任意写出一个。)
三. 解答题:本大题共6小题,共74分。解答应写出文字说明、证明过程或演算步骤。
18.(理科作)(本小题满分12分)
已知![]() ,求使
,求使
![]() 成立的自变量x的取值范围。
成立的自变量x的取值范围。
19.(文科作)(本小题满发12分)
解关于x的不等式:
![]()
20.(本小题满分12分)
已知:复数![]() ,求:
,求:![]() 的值。
的值。
21.(本小题满分12分)
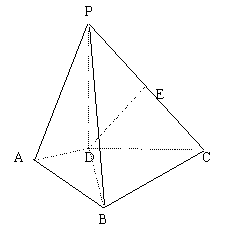
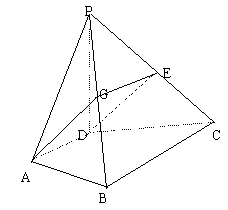
已知:如图,![]() 平面ABCD,
平面ABCD,![]() ,
,![]() 。
。
(I)求PB与平面PDC所成角的大小;
(II)求二面角D—PB—C的正切值;
(III)(理科作)若![]() ,求证平面
,求证平面![]() 平面PBC。
平面PBC。
(IV)(文科作)若![]() ,E为PC中点,求证DE//平面PAB。
,E为PC中点,求证DE//平面PAB。
22.(理科作)(本小题满分12分)
已知椭圆的两个焦点分别为![]() ,
,![]() ,离心率
,离心率![]() 。
。
(I)求椭圆方程;
(II)一条不与坐标轴平行的直线![]() 与椭圆交于不同的两点M、N,且线段MN中点的横坐标为
与椭圆交于不同的两点M、N,且线段MN中点的横坐标为![]() ,求直线
,求直线![]() 倾斜角的取值范围。
倾斜角的取值范围。
23.(文科作)(本小题满分12分)
把椭圆![]() 绕它的中心旋转
绕它的中心旋转![]() 后,再沿x轴方向平行移动,使变换后的椭圆截直线
后,再沿x轴方向平行移动,使变换后的椭圆截直线![]() 所得的线段长为
所得的线段长为![]() ,试写出变换后的椭圆方程。
,试写出变换后的椭圆方程。
24.(本小题满分12分)
用洗衣机洗衣时,洗涤并甩干后进入漂洗阶段。漂洗阶段由多次漂洗和甩干组成,每次漂洗 后可使残留物均匀分布,每次甩干后(包括洗涤后的甩干)衣物中的残留水份(含有残留物)的重量相同,设计时,将漂洗的总用水量定为a千克,漂洗并甩干的次数定为3次。为使漂洗后衣物中的残留物最少,怎样确定每次漂洗的用水量?并写出你的数学依据。
[注:为了便于解决问题,可参考以下各量的字母表示。设每次甩干后衣物中的残留水份(含有残留物)的重量为m,洗涤并甩干后衣物中的残留物(不含水份)为![]() ,三次漂洗并甩干后衣物中的残留物(不含水份)分别为
,三次漂洗并甩干后衣物中的残留物(不含水份)分别为![]() ,三次用水量分别为
,三次用水量分别为![]() 。(以上各量单位皆为千克)]
。(以上各量单位皆为千克)]
25.(理科作)(本小题满分14分)
数列![]() 中,前
中,前![]() 项和
项和![]() 其中
其中![]() 是常数,且
是常数,且![]() 。
。
(I)求![]() 的通项公式
的通项公式![]() ,并证明
,并证明![]() ;
;
(2)令![]() ,试判断数列
,试判断数列![]() 中任意相邻两项的大小。
中任意相邻两项的大小。
26.(文科作)(本小题满分14分)
已知数列![]() 是等差数列,
是等差数列,![]() ,前n项和为
,前n项和为![]() ;数列
;数列![]() 是等比数列,前n项和为
是等比数列,前n项和为![]() ,若
,若![]() 。
。
(I)求![]() 和
和![]() 的通项公式;
的通项公式;
(II)判断是否存在最小的自然数![]() ,使得大于
,使得大于![]() 的一切自然数n,总有
的一切自然数n,总有![]() 成立,并给出你的证明。
成立,并给出你的证明。
『答案』
一. 1. B 2. A 3. D 4. B 5. A 6. A 7. A 8. B 9. A 10. C
11. D 12. D 13. C
二. 14. 12
15. ![]()
16. ![]()
17. 截面AB1D1,或截面ACD1,或截面AB1C。(注:未写截面二字不扣分)
三.
18. 解:![]()

当![]() 时
时
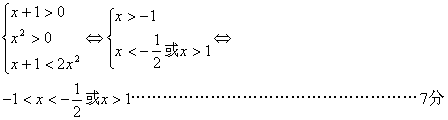
当![]() 时
时
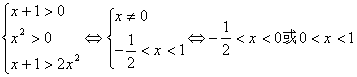
综上:当![]() 时,不等式的解为
时,不等式的解为![]()
当![]() 时,不等式的解为
时,不等式的解为![]() …………………12分
…………………12分
19. 解:![]()
![]() ………………………………………………2分
………………………………………………2分
当![]() 时
时

当![]() 时
时
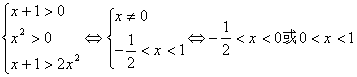
综上:当![]() 时,不等式的解为
时,不等式的解为![]()
当![]() 时,不等式的解为
时,不等式的解为![]() …………………12分
…………………12分
20. 解:由已知
![]()
即![]()
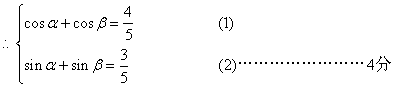
由(1)得 ![]()
由(2)得 ![]() …………………………8分
…………………………8分
两式相除,得![]() ……………………………………10分
……………………………………10分
 ………………12分
………………12分
评分标准说明:
由复数相等的充要条件转化为两个三角等式各2分。
两次和差化积各2分。求出![]() 占2分。
占2分。
用正切倍角公式计算正确占2分。两个复数的三角形式写对可各给1分。
21.(I)解:由![]() 平面ABCD,BC
平面ABCD,BC![]() 平面ABCD,得
平面ABCD,得![]() 。
。
由![]() ,得
,得![]() 。
。
又![]() ,则
,则![]() 平面PDC……………………2分
平面PDC……………………2分
所以![]() 为直线PB与平面PDC所成的角
为直线PB与平面PDC所成的角
令![]() ,则
,则![]() ,
,![]() ,可求出
,可求出![]() 。………………3分
。………………3分
由![]() 平面PDC,PC
平面PDC,PC![]() 平面PDC,得
平面PDC,得![]() 。
。
在![]() 中,由
中,由![]() 得
得![]()
即直线PB与平面PDC所成的角为![]() ……………………………………4分
……………………………………4分
(II)解法(一):
取PC中点E,连DE,则![]() 。
。
由BC![]() 平面PDC,BC
平面PDC,BC![]() 平面PBC
平面PBC
得平面PDC![]() 平面PBC。
平面PBC。
则DE![]() 平面PBC。…………………………………………………………5分
平面PBC。…………………………………………………………5分
作![]() 于F,连DF
于F,连DF
由三垂线定理,得![]()
则![]() 为二面角D—PB—C的平面角…………………………………7分
为二面角D—PB—C的平面角…………………………………7分
在![]() 中,求得
中,求得![]()
在![]() 中,求得
中,求得![]()
在![]() 中,
中,![]()
即二面角D—PB—C大小的正切值为![]() ………………………………8分
………………………………8分
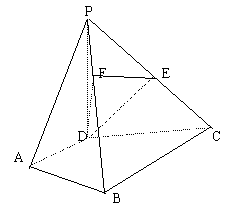
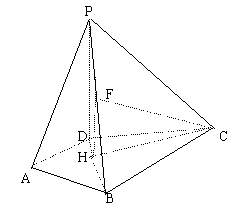
解法(二):
由![]() 平面ABCD,PD
平面ABCD,PD![]() 平面PDB
平面PDB
得平面![]() 平面ABCD
平面ABCD
作![]() 于H
于H
则![]() 平面PDB…………………………………………………………5分
平面PDB…………………………………………………………5分
作![]() 于F,连CF
于F,连CF
由三垂线定理得![]()
则![]() 为二面角D—PB—C的平面角………………………………7分
为二面角D—PB—C的平面角………………………………7分
在等腰![]() 中,求出斜边上的中线
中,求出斜边上的中线![]()
在![]() 中,求出
中,求出![]() ,可进一步求出斜边上的高
,可进一步求出斜边上的高![]()
在![]() 中,求出
中,求出![]()
![]()
即二面角D—PB—C大小的正切值是![]() …………………………………8分
…………………………………8分
(III)证:取PB中点G,连AG和EG
由三角形中位线定理得![]()
由已知,AD//BC,![]()
则四边形AGED为平行四边形
![]() ………………………………………………………………10分
………………………………………………………………10分
由(II)的解法(一),已证出![]() 平面PBC
平面PBC
![]() 平面PBC
平面PBC
又![]() 平面PAB
平面PAB
![]() 平面PAB
平面PAB![]() 平面PBC…………………………………………………12分
平面PBC…………………………………………………12分
(IV)证:取PB中点G,连AG和EG
由三角形中位线定理得![]()
由已知,AD//BC,![]()
![]()
则四边形AGED为平行四边形
![]() ………………………………………………………………10分
………………………………………………………………10分
又![]() 平面PAB,DE
平面PAB,DE![]() 平面PAB
平面PAB
![]() 平面PAB……………………………………………………12分
平面PAB……………………………………………………12分
22. 解:(I)设椭圆方程为![]()
由已知,![]()
由![]() 解得
解得![]()
![]() 为所求………………………………………3分
为所求………………………………………3分
(II)设直线![]() 的方程为
的方程为![]()
解方程组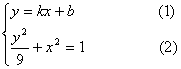
将(1)代入(2)并化简,得![]() ……………4分
……………4分
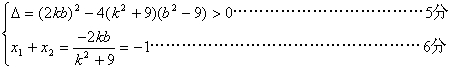
由于![]()
化简后,得
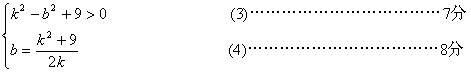
将(4)代入(3)化简后,得![]() ………………………………9分
………………………………9分
解得![]()
![]() ………………………………………………………10分
………………………………………………………10分
由已知,倾斜角不等于![]()
![]()
![]() 倾斜角的取值范围是
倾斜角的取值范围是![]() ……………………12分
……………………12分
23. 解:旋转后的椭圆方程为![]() ………………………3分
………………………3分
设平移后的椭圆方程为![]() …………………………4分
…………………………4分
解方程组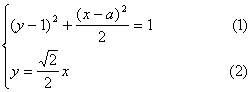
将(2)代入(1)后,得![]()
化简后,得
![]() ……………………7分
……………………7分
由椭圆截直线所得线段长为![]() 有
有
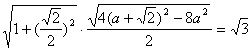 …………………………………9分
…………………………………9分
解得![]() 或
或![]() ,并且都使方程(3)有实根
,并且都使方程(3)有实根
![]() 变换后的椭圆方程为:
变换后的椭圆方程为:![]() ………………………………11分
………………………………11分
或![]() ………………………………………………12分
………………………………………………12分
24. 解:
由已知,得![]() ……………………………………………………4分
……………………………………………………4分
解得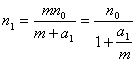 …………………………………………………5分
…………………………………………………5分
同样可得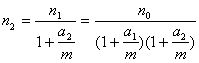 …………………………………6分
…………………………………6分
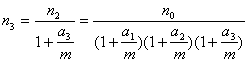 ……………………………………7分
……………………………………7分
由![]() 及平均值定理,得
及平均值定理,得
![]()
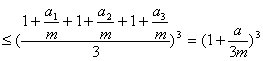
当且仅当![]() 时等号成立………………………………………10分
时等号成立………………………………………10分
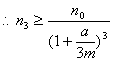
当且仅当![]() 时等号成立………………………………………11分
时等号成立………………………………………11分
则将a千克的水平均分成三次使用可使衣物上的残留物最少………………12分
25. 解:(I)![]() ………………………………………………………1分
………………………………………………………1分
![]()
![]() (
(![]() )…………………………………………3分
)…………………………………………3分
当![]() 时也能满足上式
时也能满足上式
![]() (
(![]() )………………………………………4分
)………………………………………4分
![]()
![]() (
(![]() )……………………………………………6分
)……………………………………………6分
(II)由(I)及对数的性质可得数列![]() 中各项皆为正值
中各项皆为正值
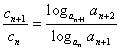
![]() ………………………………………………………7分
………………………………………………………7分
![]() ………………………………………………9分
………………………………………………9分
![]() ……………………………………………………10分
……………………………………………………10分
![]() ……………………………………11分
……………………………………11分
![]() ……………………………………………………13分
……………………………………………………13分
又![]()
![]()
![]() ………………………………………………14分
………………………………………………14分
26. 解:(I)设![]() 的公差为d,
的公差为d,![]() 的公比为
的公比为![]() ,由已知得方程组:
,由已知得方程组:
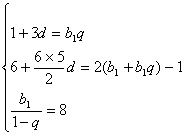 化简后,得
化简后,得
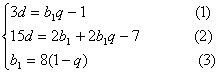 ………………………………………2分
………………………………………2分
将(1)(3)代入(2)并化简后,得![]()
解得![]() 或
或![]() (舍)
(舍)
将![]() 代入(1)(3)分别求出
代入(1)(3)分别求出![]() ……………………………5分
……………………………5分
则![]() ……………………………………………7分
……………………………………………7分
(II)![]() ……………………………………………………8分
……………………………………………………8分
考查不等式![]() ,当
,当![]() 时不成立,
时不成立,![]() 时成立,猜想取
时成立,猜想取![]()
………………………………………………………………………………………10分
用数学归纳法证明如下:
(1)当![]() 时,
时,![]() ,不等式成立。
,不等式成立。
(2)假设![]() 时,不等式成立,即
时,不等式成立,即![]() 。
。
则当![]() 时,
时,![]() ,不等式也成立。
,不等式也成立。
综合(1)(2),对任意![]() 的自然数n,不等式
的自然数n,不等式![]() 成立。……12分
成立。……12分
评分标准说明:列方程组正确2分,解方程组每个解正确各1分。通项公式写对各1分,代入计算![]() 正确占1分。猜想
正确占1分。猜想![]() 占2分,用数学归纳法证明占4分。
占2分,用数学归纳法证明占4分。