第一学期高三数学综合测试卷
本试卷分第I卷（选择题）和第II卷（非选择题）两部分，共150分，考试时间120分钟。
第I卷（选择题 共60分）
参考公式：
如果事件A、B互斥，那么P(A+B)=P(A)+P(B)
如果事件A、B相互独立，那么P（A·B）=P（A）·P（B）
如果事件A在一次试验中发生的概率是P，那么n次独立重复试验中恰好发生k次的概率
pn(k)=cnkpk(1－p)n－k
正棱锥、锥台的侧面积公式
S锥侧=
cl
其中c表示底面周长，l表示斜高或母线长球体的体积公式
V球=
其中R表示球的半径
一、选择题：本大题共12个小题；每小题5分，共60分，在每小题给出的四个选项中，有且只有一项是符合题目要求的。
1．函数是y=sin2x是 （ ）
A.
最小正周期为
的奇函数
B.最上正周期为的偶函数
C.最小正周期为2的奇函数
D.最小正周期为2的偶函数
2.集合P
只有一个子集，那么实数k的取值范围是（ ）
A．（－∞,1）
B．
C．（1，+∞）
D．（－∞，＋∞）
3．如果a1,a2,a3,a4,a5,a6的平均数（期望）为3，那么2(a1－3)、2(a2－3)、2（a3－3）、2（a4－3）、2(a5－3)、2(a6－3)的平均数（期望）是（ ）
A．0 B．3 C．6 D．12
4．已知函数f(x)=2x3－
（m为常数）图象上A处的切线与直线x－y+3=0的夹角为45°，则A点的横坐标为（ ）
A．0 B．1
C．0或
D．1或
5．已知数列
（n∈N）中，a1=1，an+1=
则这个数列的第n项an为（ ）
A．2n－1
B．2n+1
C．
D．
6.函数f(x)=ax－1的反函数的图象经过点（4，2），则f－1(2)的值是（ ）
A．－
B．
C．2 D．4
7．已知一个简单多面体的各个顶点都有三条棱，那么2F－V=（ ）
A．12 B．8 C．4 D．2
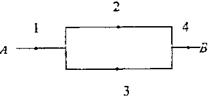8．如图所示，在A、B间有四个焊接点，若焊接点脱落，则可能导致电路不通。今发现A、B之间线路不通，则焊接点脱落的不同情况有（ ）
A．10 B．13 C．15 D．17
9．已知x>1,则x+
取得最小值时x的值为（ ）
A．4
B．2
C．3
D．
10．若a、b为任意实数，且a>b，则有（ ）
A．a2>b2
B．
C．lg(a－b)>0
D．
11.函数f(x)=－x
为奇函数的充要条件是（
）
A．b=0 B．a=0 C．ab=0 D．a2+b2=0
12.已知函数y=f(x)(x∈R)满足f(x+1)=f(x－1)且x∈[－1,1]时，f(x)=x2，则y=f(x)与y=log5x的图象的交点个数为（ ）
A．2 B．3 C．4 D．5
第II卷（非选择题 共90分）
二、填空题：本大题共4小题；每小题4分，共16分。把答案填在答卷纸上。
13．已知sin
，则cos2
=_____________________。
14．函数f(x)=ax(a>0且x≠1)在[1，2]中的最大值比最小值大
，则a的值为__________________________。
15．在等差数列中，满足3a4=7a7，且a1>0，Sn是数列的前n项和。若Sn取得最大值，则n=_________________________。
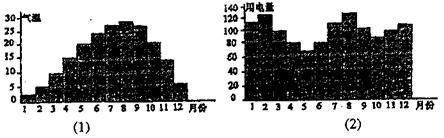
16．一般地，家庭用电量y(千瓦)与气温x（℃）有函数关系y=f(x)。图（1）表示某年12个月中每月的平均气温，图（2）表示某家庭在12个月中每月的用电量。试在数集A=
中确定一个最小值x1和最大值x2，使y=f(x)是[x1,x2]上的增函数，则区间[x1,x2]=_______________________。
三、解答题：本大题6分题，共74分。解答应写出文字说明，证明过程或演算步聚。
17．（本小满分12分）
已知P:
的必要而不充分条件，求m的取值范围。
18．（本小题满分12分）
设a>0, f(x)=
是R上的偶函数。
（1）求a的值；
（2）证明f(x)在（0，+∞）上是增函数。
19．（本小题满分12分）
解关于x的不等式
。
20．（本小题满分12分）
已知
若函数f(x)=ax2－2x+1在区间[1，3]上的最大值为M（a），最小值为N（a），令g(a)=M(a)－N(a).
(1)求g(a)的函数表达式；
（2）判断函数g(a)在区间
上的单调性，并求出g(a)的最小值。
21．（本小题满分12分）
我国西部某地区去年各季度某农产品的价格如下表：
| 季度 | 第一季度 | 第二季度 | 第三季度 | 第四季度 |
| 每担售价 （单位：元） | 203.5 | 201.5 | 195.5 | 200.5 |
今年按某农贸公司计划按去年各季度市场价的“最佳近似值m”(m是与上表中各售价差的平方和取最小值时的值)收购该种农产品，并按每100元纳税10元（又称征税率为10个百分点），计划可收购a万担。政府为了鼓励收购公司多收购这种农产品，决定征税率降低x个百分点，预测收购量可增加2x个百分点。
（1）根据题中条件填空，m=_____________________(元/担)；
（2）写出税收y(万元)与x的函数关系式；
（3）要使此项税收在税率调节后不少于原计划税收的83.2%，试确定x的取值范围。
22．（本小题满分14分）
已知函数fn(x)=a0+a1x+a2x2+a3x3+……+anxn(n∈N*)，且y=fn(x)的图象经过点（1，n2）,数列(n∈N*)为等差数列。
（1）求数列通项公式；
（2）当n为奇数时，设gn(x)=
,是否存在整数m和M，使不等式m<gn()<M恒成立，若存在，求出M－m的最小值；若不存在，说明理由。
【参考答案】
一、选择题：本大题共12个小题；每小题5分，共60分。
1．A 2.B 3.A 4.C 5.C 6.B 7.C 8.B 9.B 10.D 11.D 12.C
二、填空题：本大题共4小题：每小题4分，共16分。
13．－
14.a=
15.9
16.[20,27.5]
三、解答题：本大题6分题，共74分。
17．（本小满分12分）
解：设不等式
的解集为A，不等式x2－2x+1－m2<0的解集为B
q的必要而不充分条件，∴A
（3分）
∵A=
（4分）
当m>0时，B=
（7分）
（注：正确解得B得1分）
当m=0时，B=
，不合题意； （8分）
当m<0时，B=
(11分)
∴m的取值范围为m≥9或m≤－9 （12分）
18．（本小题满分12分）
解：（1）依题意，对一切x∈R有f(x)=f(－x). 即
∴（a－
）(
)=0对一切x
R成立。
（3分）
由此得a
,即a2=1, 又∵a>0, ∴a=1
(5分)
（2）设任意x1、x2(0,+
),且x1<x2,则f(x1)－f(x2)
=e
,
=
=
(8分)
∵0<x1<x2
∴x2－x1>0, x1+x2>0
∴e
1－
（10分）
又∵
∴f(x1)－f(x2)<0
即f(x)在（0,+∞）上是增函数。 （12分）
19．（本小题满分12分）
解：按照解分式不等式的一般步骤求解：先移项、通分，再因式分解。
原不等式即
即
（1分）
（1）
当a>1时，a－1>0，原不等式可化为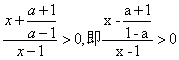
∵a>1，
∴
∴原不等式解集为
（5分）
（2）当a=1时，原不等式即
∴解集为
（7分）
（3）当0<a<1时，原不等式可化为
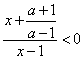，即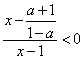
，
∵
∴
∴原不等式解集为
（12分）
20．（本小题满分12分）
解：（1）∵
∴f(x)的图象为开口向上的抛物线，且对称轴为x=
∴f(x)有最小值N（a）=1－.
（2分）
当2
f(x)有最大值，M(a)=f(1)=a－1;
当1
f(x)有最大值，M(a)=f(3)=9a－5;
∴g(a)=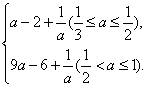
(6分)
（2）
设
∴g(a1)>g(a2),
∴g(a)在[
]上是减函数。（8分）
设
∴g(a1)<g(a2)∴g(a1)在（
上是增函数。
（10分）
∴当a=时，g(a)有最小值。
（12分）
21．（本小题满分12分）
（1）200；
（2）降低税率后的税率为（10－x）%，农产品的收购量为a(1+2x%)万担，收购总金额200·a(1+2x%). 依题意，
y=200a(1+2x%)·(10－x)% (5分)
=
=
(0<x<10)
(7分)
（3）原计划税收为200a×10%=20a (万元).
依题意，得
（9分）
即x2+40x－84≤0，解得－42≤x≤2, 又0＜x＜10,
∴0<x≤2. (12分)
22．（本小题满分14分）
解：（1）据题意：fn(1)=n2 即a0+a1+a2+a3+…+an=n2
令n=1 则a0+a1=1, a1=1－a0
令n=2 则a0+a1+a2=22,a2=4－(a0+a1)=4－1=3
令n=3 则a0+a1+a2+a3=32, a3=9－(a0+a1+a2)=9－4=5
为等差数列
∴d=a3－a2=5－3=2
a1=3－2=1 a0=0 an=1+(n－1)·2=2n－1 (6分)
（2）由（1）fn(x)=a1x1+a2x2+a3x3+…+anxn
n为奇数时，fn(－x)=－a1x1+a2x2+a3x3+…+an－1xn－1+anxn (7分)
gn(x)=
gn()=1·()3+5·()5+…+(2n－5)()n－2+(2n－1)()
相减得
9分
∴gn()=
n为奇数
（10分）
令cn=
cn+2－cn=
,n为奇数
∴cn+2≤cn, cn随n增大而减小
又
随n增大而减小
∴gn()为n的增函数，当n=1时，gn()=
而
∴
（12分）
∴使m<gn()<M恒成立的整数m的最大值为0，M最小值为5
M－m的最小值为5 （14分）
注：用其他的方法，求出m的最大值或M的最小值之一，可得2分