第一学期期中考试高三年级数学试卷
一、选择题(本大题共12小题,每题5分,共60分 )
1、函数![]() 的定义域为
( )
的定义域为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2、设平面上有四个互异的点![]() 、
、![]() 、
、![]() 、
、![]() ,已知
,已知![]() ,则
,则![]() 的形状是
( )
的形状是
( )
A.直角三角形 B.等腰三角形 C.等腰直角三角形 D.正三角形
3、设函数![]() (
(![]() 为实常数)在区间
为实常数)在区间![]() 上的最小值为
上的最小值为![]() ,则
,则![]() 的值等于
( )
的值等于
( )
A.4
B.![]() C.
C.![]() D.
D.![]()
4、已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,则
,则![]() 等于
( )
等于
( )
A.18 B.36 C.54 D.72
5、已知集合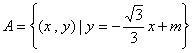 ,集合
,集合![]() ,若
,若![]() 中含有两个元素,则实数
中含有两个元素,则实数![]() 的取值范围是
( )
的取值范围是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.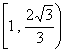
6、已知实数![]() 且
且![]() ,则
,则![]() 的取值范围是 ( )
的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7、已知![]() 是定义在
是定义在![]() 上的奇函数,且满足
上的奇函数,且满足![]() ,当
,当![]() 时,
时,![]() ,则使
,则使![]() 的
的![]() 值等于
( )
值等于
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() (所有
(所有![]() )
)
8、把函数![]() 的图像沿向量
的图像沿向量![]() 平移后,得到函数
平移后,得到函数![]() 的图像,则
的图像,则![]() 的坐标为
( )
的坐标为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9、若直线![]() (
(![]() ),始终平分圆
),始终平分圆![]() 的周长,则
的周长,则![]() 的最小值是
( )
的最小值是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
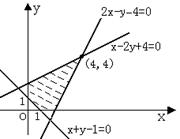 10、已知动点
10、已知动点![]() 所在的区域是如图所示的阴影部分(包括边界),则目标函数
所在的区域是如图所示的阴影部分(包括边界),则目标函数![]() 的最小值和最大值分别为 ( )
的最小值和最大值分别为 ( )
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
11、等比数列![]() 中,
中,![]() ,公比
,公比![]() ,用
,用![]() 表示它的前
表示它的前![]() 项之积:
项之积:![]() ,则
,则![]() ,
,![]() ,…中最大的是
( )
,…中最大的是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
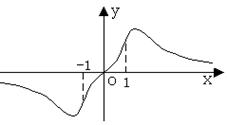 12、若函数
12、若函数![]() 的图像如图所示,则实数
的图像如图所示,则实数![]() 的取值范围为
( )
的取值范围为
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二、 填空题(本大题共4小题,每题4分,共16分 )
13、![]()
![]() ,则
,则![]()
14、过点![]() ,并被圆
,并被圆![]() 截得的弦长为
截得的弦长为![]() 的直线方程是
的直线方程是
15、已知命题![]() :不等式
:不等式![]() 的解集为
的解集为![]() ,命题
,命题![]() :
:![]() 是减函数,若
是减函数,若![]() 或
或![]() 为真命题,
为真命题,![]() 且
且![]() 为假命题,则实数
为假命题,则实数![]() 的取值范围是
的取值范围是
16、定义符号函数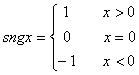 ,
,
则不等式![]() 的解集为
的解集为
三、 解答题(本大题共6小题,共74分)
17、(本题满分12分)
在![]() 中,
中,![]() 、
、![]() 、
、![]() 分别是角
分别是角![]() 、
、![]() 、
、![]() 对边,
对边,![]()
(1)求角![]() 的度数
的度数
(2)若![]() ,
,![]() ,求
,求![]() 和
和![]() 的值
的值
18、(本题满分12分)
平面直角坐标系内有两点![]() ,
,![]() ,
,![]() ,
,![]() 为坐标原点,
为坐标原点,
(1)令向量![]() 和
和![]() 的夹角为
的夹角为![]() ,试用
,试用![]() 的函数
的函数![]() 表示
表示![]()
(2)求![]() 的取值范围
的取值范围
19、(本题满分12分)
已知数列![]() 的前几项和
的前几项和![]() ,数列
,数列![]() 的首项
的首项![]() ,且
,且![]()
![]()
(1)求数列![]() 和
和![]() 通项公式
通项公式
(2)是否存在自然数![]() ,对一切不小于
,对一切不小于![]() 的自然数
的自然数![]() ,恒有
,恒有![]() ,若存在,求出
,若存在,求出![]() ;若不存在,说明理由。
;若不存在,说明理由。
20、(本题满分12分)
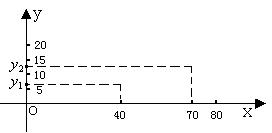 行驶中的汽车,在刹车时由于惯性作用,要继续往前滑行一段距离才能停下,这段距离叫刹车距离。在某种路面上,某种型号汽车的刹车距离
行驶中的汽车,在刹车时由于惯性作用,要继续往前滑行一段距离才能停下,这段距离叫刹车距离。在某种路面上,某种型号汽车的刹车距离![]() (
(![]() )与汽车的车速
)与汽车的车速![]() (
(![]() )满足下列关系:
)满足下列关系:![]() (
(![]() 为常数,
为常数,![]() )。我们做过两次实验,有关数据如图所示,其中
)。我们做过两次实验,有关数据如图所示,其中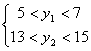
(1)求出![]() 的值
的值
(2)要求刹车距离不超过![]() ,则行驶的最大速度应为多少?
,则行驶的最大速度应为多少?
21、(本题满分12分)
已知定点![]() ,
,![]() ,动点
,动点![]() 满足
满足![]() 等于点
等于点![]() 到点
到点![]() 距离平方的
距离平方的![]() 倍。
倍。
(1)试求动点![]() 的轨迹方程,并说明方程所表示的曲线,
的轨迹方程,并说明方程所表示的曲线,
(2)当![]() 时,求
时,求![]() 的最大值和最小值
的最大值和最小值
22、(本题满分14分)
已知![]() ,
,![]() ,
,
(1)当![]() 时,求证:
时,求证:![]()
(2)证明函数![]() 的图像关于点
的图像关于点![]() 成中心对称图形;
成中心对称图形;
(3)我们利用函数![]() 构造一个数列
构造一个数列![]() ,方法如下:对于给定的定义域中的
,方法如下:对于给定的定义域中的![]() ,令
,令![]() ,
,![]() ,
,![]() ,
,![]() ,在上述构造数列的过程中,如果
,在上述构造数列的过程中,如果![]() (
(![]() 、
、![]() 、
、![]() 、
、![]() )在定义域中,构造数列的过程将继续下去,如果
)在定义域中,构造数列的过程将继续下去,如果![]() 不在定义域中,则构造数列的过程停止。
不在定义域中,则构造数列的过程停止。
(Ⅰ)如果可以用上述方法构造出一个常数数列![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
(Ⅱ)如果取定义域中任一值作为![]() ,都可以用上述方法构造出一个无穷数列
,都可以用上述方法构造出一个无穷数列![]() ,求实数
,求实数![]() 的值。
的值。
参考答案:
一、BCDD AACAC CC
二、13.![]() 14.
14.![]() 或
或![]()
15.![]() 16.
16.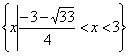
三、17.①![]() ;②
;②![]() 或
或![]()
18.①![]() ; ②
; ②![]()
19.①![]()
![]() ②存在
②存在![]() ,使
,使![]()
20.①![]() ②80km/h
②80km/h
21. ①![]()
当![]() 时
时![]() ,轨迹为抛物线;
,轨迹为抛物线;
当![]() 时,轨迹为以
时,轨迹为以![]() 为圆心,
为圆心,![]() 为半径的圆。
为半径的圆。
②![]()
22.①略②略③(ⅰ)![]() 或
或![]() ;(ⅱ)
;(ⅱ)![]()