调研测试题高三数学参考答案及评分标准
说明:
1.本解答指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.
2.对计算题当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.
3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.
4.只给整数分数,选择题和填空题不给中间分数.
一.选择题:CACB(理(文 BDCC(理(文 BC
二.填空题:13.(理)-1
(文)27 14.960x3 15.![]() 16.(理)①③④ (文)③
16.(理)①③④ (文)③
三.解答题
17.解:sin
A ![]() +sin C
+sin C ![]() =
=![]() sin B 2分
sin B 2分
sin A+sin A
cos C+sin
C+sin
C cos A=3 sin B
sin A+sin C+sin (A+C)=3
sin B,∴sin
A+sin
C=2sin
B,即2b=a+c 6分
由余弦定理,得
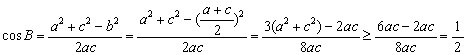 10分
10分
∵
0<B<![]() 且函数y=cos x在[0,
且函数y=cos x在[0,![]() ]上是减函数
]上是减函数
∴0<B≤![]() ,即B的范围是(0,
,即B的范围是(0,![]() ]. 12分
]. 12分
18.(1)解:由题知f / (x)=3x2+2ax+b=0的两根为![]() 和1 2分
和1 2分
∴由韦达定理有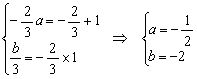 4分
4分
(2)解:由(1)知![]()
当x∈[-1,-![]() )时,f / (x)>0;x∈(-
)时,f / (x)>0;x∈(-![]() ,1)时,f / (x)<0;x∈(1,2]时,f / (x)>0
,1)时,f / (x)<0;x∈(1,2]时,f / (x)>0
∴当x=-![]() 时,f (x)有极大值
时,f (x)有极大值![]() 8分
8分
又f (2)=2+c>![]() ,f (-1)=
,f (-1)=![]() +c<
+c<![]()
∴x∈[-1,2]时,f (x)的最大值为f (2)=2+c 10分
∵对x∈[-1,2],f (x)<c2恒成立
∴c2>2+c,解得c<-1或c>2. 12分
|
|
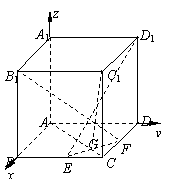
19.(1)证:以A为原点,分别以![]() 为x轴、y轴、z轴建立空间直角坐标系,
为x轴、y轴、z轴建立空间直角坐标系,
设BE=x,则有B1(a,0,a),D1(0,a,a),
E(a,x,0),F(a-x,a,0)
2分
∴![]()
∴![]()
因此,B1F⊥D1E.
4分
(2)解:![]() 6分
6分
当![]() 时,三棱锥C1-CEF的体积最大,这时E、F分别为BC、CD的中点 8分
时,三棱锥C1-CEF的体积最大,这时E、F分别为BC、CD的中点 8分
连结AC交EF于G点,连结C1G,则AC⊥EF
由三垂线定理知C1G⊥EF,∴∠C1GC是二面角C1-EF-C的平面角 10分
∵![]() ,∴
,∴![]()
即二面角C1-EF-C的大小为![]() . 12分
. 12分
20.(理科)解:设保险公司要求顾客交x元保险金,若以x 表示公司每年的收益额,则x是一个随机变量,其分布列为:
| x | x | x-a |
P | 1-p | p |
6分
因此,公司每年收益的期望值为Ex =x(1-p)+(x-a)·p=x-ap. 8分
为使公司收益的期望值等于a的百分之十,只需Ex =0.1a,即x-ap=0.1a,
故可得x=(0.1+p)a. 10分
即顾客交的保险金为 (0.1+p)a时,可使公司期望获益10%a. 12分
(文科)(1)解:这批食品不能出厂的概率是:
P=1-0.85-![]() ×0.84×0.2≈0.263. 4分
×0.84×0.2≈0.263. 4分
(2)解:五项指标全部检验完毕,这批食品可以出厂的概率是:
P1=![]() ×0.2×0.83×0.8 8分
×0.2×0.83×0.8 8分
五项指标全部检验完毕,这批食品不能出厂的概率是:
P2=![]() ×0.2×0.83×0.2 10分
×0.2×0.83×0.2 10分
由互斥事件有一个发生的概率加法可知,五项指标全部检验完毕,才能确定这批产品是否出厂的概率是:P=P1+P2=![]() ×0.2×0.83=0.4096. 12分
×0.2×0.83=0.4096. 12分
21.(理科) (1) 解:∵f 1(0)=2 ∴ ![]() 1分
1分
∵![]() ,
,
∴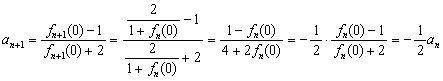 3分
3分
∴数列{an}是首项为![]() ,公比为
,公比为![]() 的等比数列,
的等比数列,![]() 4分
4分
(2)证:![]()
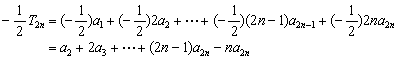
![]() 6分
6分
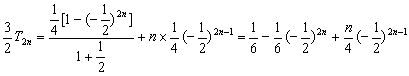
![]() 8分
8分
![]()
当n=1时,22n=4,(2n+1)2=9,∴9T2n<Qn
当n=2时,22n=16,(2n+1)2=25,∴9T2n<Qn
当n≥3时,![]() ,∴9T2n>Qn 12分
,∴9T2n>Qn 12分
(文科)(1)解:a1=f (d-1)=(d-2)2,a3=f (d+1)=d 2
∴d2=(d-2)2+2d,解得d=2,故an=2n-2 3分
b1=f (q+1)=q2,b3=f (q-1)=(q-2) 2
∴(q-2) 2=q2×q2,解得q=-2,故bn=(-2)n+1 6分
(2)解:![]() 8分
8分
∴![]() 10分
10分
∴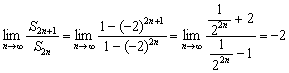 . 12分
. 12分
22.(理)(1)证:∵f (x)的图象与x轴有两个不同的公共点
∴方程f (x) =0有两个不同的实根
∵f (c)=0,∴c是方程f (x)=0的一个根
设方程的另一根为x0,则![]() 2分
2分
若![]() ,由0<x<c时,f (x)>0 得:
,由0<x<c时,f (x)>0 得:![]() ,与
,与![]() 矛盾 4分
矛盾 4分
又方程f (x)=0有两个不同的实根,∴![]() ≠c,因此
≠c,因此![]() 6分
6分
(2)证: f (c)=0 Û ac+b+1=0,∴b=-1-ac<-1
∵![]() ,∴
,∴![]() ,∴-2<b<-1 . 10分
,∴-2<b<-1 . 10分
(3)证:∵0<1<c,∴f (1)>0,即a+b+c>0 Þ b>-a-c 12分
![]()
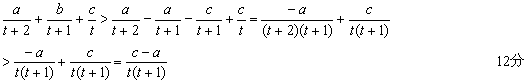
又∵![]() ,c>1 ∴
,c>1 ∴![]() Þ a<c
Þ a<c
∴![]() ,故
,故![]()
(文)(1)证明:任取x1,x2(-∞,0),且x1<x2,则-x1,-x2∈(0,+∞),且-x1>-x2
∵f (x)在(-∞,0)∪(0,+∞)上是奇函数
∴f (-x1)=-f (x1), f (-x2)=-f (x2) ① 2分
∵f (x)在(0,+∞)上是增函数
∴f (-x1)>f (-x2) ②
由①②得 -f (x1)>-f (x2),即f (x1)<f (x2)
∴f (x)在(-∞,0)上是增函数. 4分
(2)解:奇函数f (x)满足f (1)=0且在(0,+∞)上是增函数
∴当x>0时,由f (x)<0得 f (x)<f (1),因而0<x<1 6分
当x<0时,由f (x)<0得 f (x)<f (1)=f (-1),因而x<-1
∴使f (x)<0的x的取值范围是(-∞,-1)∪(0,1). 8分
(3)由(2)知f [g (x)]<0即g (x)<-1或0<g (x)<1
由题得![]() 10分
10分
由g (x) <-1得:-x2+mx+1-2m<-1
即![]() 12分
12分
∵![]() ,∴
,∴![]()
当且仅当![]() ,即
,即![]() 时,等号成立
时,等号成立
从而![]() 14分
14分