二、换元法（课时10）
一、知识提要
解数学题时，把某个式子看成一个整体，用一个变量去代替它，从而使问题得到简化，
这叫换元法.
换元的方法有：局部换元、三角换元、均值换元等.
二、例题讲解
例1．（1）已知：
，求
.
（2）设实数
、
满足
，则
的取值范围是_________.
（3）方程
的解集是______________.
解：（1）
；
（2）设
，则
或
；
（3）令
=
，可得原方程的解集为
.
例2．（1）函数
的值域是_____________.
(2)已知：数列
的
，前
项和为
，
.求的通项公式.
解：（1）令
，
，则
， ∴
.
（2）由，知
，
∴
，即
∴
，令
，则
∵，
，∴
，
，即
.
两边除以
得：
，令
，则有
，
∴
，代入得： 
.
例3．实数x、y满足4x
－5xy＋4y＝5 （ ①式） ，设S＝x＋y，求
＋
的值.（93年全国高中数学联赛题）
方法1：设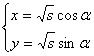
代入①式得： 4S－5S·sin
cos＝5
解得 S＝
；
∵ -1≤sin2α≤1 ∴ 3≤8－5sin2α≤13 ∴ 
≤
≤
∴ ＋＝
＋
＝
＝
方法2：由S＝x＋y，设x＝
＋t，y＝－t，t∈[－
，]，
则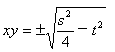
代入①式得：4S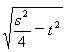±5
=5，
移项平方整理得 100t+39S－160S＋100＝0 .
∴
39S－160S＋100≤0 解得：≤S≤
∴ ＋＝＋＝＝
方法3：（和差换元法）设x＝a＋b，y＝a－b，代入①式整理得3a＋13b＝5 ，求得a∈[0,
]，所以S＝(a－b)
＋(a＋b)＝2(a＋b)＝＋
a∈[,]，再求＋的值.
三、同步练习
1．
的最大值是__
＋
___.
2．已知数列中，
a
＝－1，则数列通项
＝_____
____.
3．已知x＋4y＝4x，则x＋y的范围是_____
______.
4．设等差数列的公差
，且
，则
的值为（C）
A. 85 B. 72.5 C. 60 D. 52.5
5．已知
，
，则
＋
的范围是__
__.
6．函数
的值域是_____
_____.
7．已知正四棱锥
的侧面与底面所成的角为
，相邻两侧面所成的角为
求
的值.
解答：0
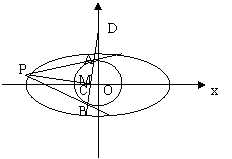
8．如图，已知椭圆
，圆
椭圆
而
、
是圆
任意切线，
、
为切点.
（1）求
中点
的轨迹方程；
|
所在直线交轴于，交轴与
，求
的最小值.
解：（1）
；
（2）
.