高考能力测试步步高数学基础训练24
基础训练24 简单的线性规划、曲线和方程
●训练指要
会画二元一次不等式表示的平面区域，理解曲线与方程的含义.并会应用曲线与方程的关系解题.
一、选择题
1. 不等式x-2y+6＞0表示的平面区域在直线x-2y+6=0的
A.右上方 B.右下方 C.左上方 D.左下方
2.方程x2＋(x2＋y2－1)2＝0的图象是
A.y轴或圆 B.两点(0，1)与(0，－1)
C.y轴或直线y＝±1 D.非上述答案
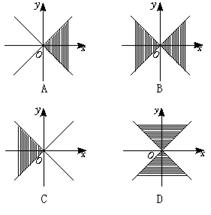
3.在直角坐标系内，满足不等式x2-y2≥0的点(x,y)的集合(用阴影表示)是
二、填空题
4.直线3x+y-3=0上位于x轴下方的一点P到直线x-y-1=0的距离为3
，则P点坐标是_________.
5.不等式组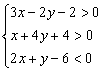
的整数解共有_________组.
三、解答题
6.画出方程2x-3+y-6=0所表示的图形，如果它与x轴围成封闭的图形，求出它的面积.
7.在由三条直线x-y+2=0,x+y-4=0,x+2y+1=0围成的三角形内求一点，使其到三直线的距离相等.
8.判断方程y2(y2-1)=x2(x2-1)所表示的曲线C，并回答下列问题：
(1)若点M(m,)与N(
，n)在曲线C上，求m、n的值.
(2)若直线x=a与曲线C有四个不同的交点，求实数a的取值范围.
高考能力测试步步高数学基础训练24答案
一、1.B 2.B 3.B
二、4.(
) 5.6
三、6.图略，封闭图形面积是18.
7.(1，
)
提示：设三角形内一点P(x,y)到三直线的距离相等，则
.利用P在直线上方或下方去绝对值后即可求得P(1,).
8.(1)m=±
(2)a∈(－1,－
)∪(－,0)∪(0, )∪(，1).
提示：(1)略
(2)已知方程化为(x+y)(x－y)(x2+y2－1)=0，它表示两相交直线和一个圆，数形结合可求得a的取值范围.