高考能力测试步步高数学基础训练34
基础训练34(A) 空间的角度与距离
●训练指要
掌握空间有关的角与距离的概念、范围、计算方法，会计算有关的距离和角.
一、选择题
1.(2001年全国高考题)一间民房的屋顶有如图三种不同的盖法：①单向倾斜；②双向倾斜；③四向倾斜，记三种盖法屋顶面积分别为P1、P2、P3.
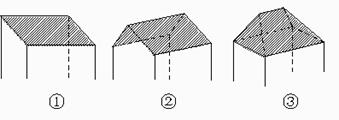
若屋顶斜面与水平面所成的角都是α,则
A.P3＞P2＞P1 B.P3＞P2=P1
C.P3=P2＞P1 D.P3=P2=P1
2.给出下列四个命题：
①如果直线a∥平面α，a
平面β，且α∥β，则a与平面α的距离等于平面α与β的距离；
②两条平行直线分别在两个平行平面内，则这两条平行直线的距离等于这两个平面间的距离；
③异面直线a、b分别在两个平行平面内，则a、b的距离等于这两个平面的距离；
④若点A在平面α内，平面α和β平行，则A到平面β的距离等于平面α与平面β的距离.
其中正确的命题的个数是
A.1 B.2 C.3 D.4
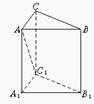3.如图，正三棱柱ABC—A1B1C1的各条棱长均相等，则AC1与平面BB1C1C所成角的余弦值等于
A.
B.
C.
D.
二、填空题
4.二面角α—l—β的面α内有一条直线a与l成45°的角，若这个二面角的平面角也是45°,则直线a与平面β成角的度数为_________.
5.三个两两垂直的平面，它们的三条交线交于一点O，点P到三个平面的距离的比为1∶2∶3，PO=2
,则P点到这三个平面的距离分别是_________.
三、解答题
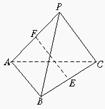
6.如图，在正三棱锥P—ABC中，侧棱长3 cm，底面边长2 cm，E是BC的中点，EF⊥PA，垂足为F.
(1)求证：EF为异面直线PA与BC的公垂线段；
(2)求异面直线PA与BC间的距离.
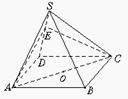7.如图，正四棱锥S—ABCD的所有棱长都相等，过底面对角线 AC作平行于侧棱SB的截面交SD于E.
(1)求AB与SC所成角的大小；
(2)求二面角E—AC—D的大小；
(3)求直线BC与平面EAC所成角的大小.
8.在棱长为a的正四面体ABCD中，M、E分别是棱BD、BC的中点，N是BE的中点，连结DE、MN，求直线DE与平面AMN间的距离.
基础训练34(B) 夹角与距离的计算
●训练指要
掌握空间有关角和距离的确定方法、范围，熟练地计算空间的角和距离.
一、选择题
1.已知点A、B、C、D的坐标分别为(-1，0，1)，(0，0，1)，(2，2，2)(0，0，3)，则
所成的角为
A.arccos(-
) B.-arccos(-)
C.arccos D.-arccos
2.α—a—β的平面角是锐角θ,α内一点A到棱a的距离为4，点A到面β的距离为3，则tanθ的值等于
A.
B.
C.
D.
3.将锐角为60°,边长为a的菱形ABCD沿较短的对角线折成60°的二面角，则AC与BD的距离为
A.a B.
C.
a
D.
二、填空题
4.在棱长为1的正方体ABCD—A1B1C1D1中,E是棱BB1的中点，P是截面ABC1D1上的一动点，则A1P+PE的最小值为_________.
5.直二面角α—l—β，线段AB，A∈α,B∈β，AB与α所成的角为30°,则AB与β所成角的取值范围是_________.
三、解答题
6.已知△ABC中，A(2，-5，3)，
=(4，1，2)，
=(3，-2，5)，求其余顶点与向量
及∠A.
7.已知空间三点A(1，2，3)，B(2，-1，5)，C(3，2，-5).
试求：(1)△ABC的面积；
(2)△ABC的AB边上的高.
8.(2003年上海春季高考题)已知三棱柱ABC—A1B1C1，在某个空间直角坐标系中，
,
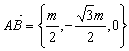={m,0,0},
={0,0,n},其中m、n＞0.
(1)证明：三棱柱ABC—A1B1C1是正三棱柱；
(2)若m=
n,求直线CA1与平面A1ABB1所成角的大小.
高考能力测试步步高数学基础训练34答案
基础训练34(A) 夹角与距离的计算参 考 答 案
一、1.D 2.C 3.A
二、4.30° 5.2、4、6
三、6.(1)BC⊥面PAE，在△PAE中EF⊥PA
(2)即EF的长为
cm
7.(1)60° (2)45° (3)30°
8.
基础训练34(B) 夹角与距离的计算参 考 答 案
一、1.A 2.C 3.A
二、4.
5.0°＜θ≤60°
三、6.设B(x,y,z),C(x1,y1,z1)
因为
=(4，1，2)
所以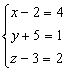
解得
因为
=(3,－2,5)
所以
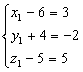，解得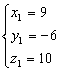
，所以C(9，－6，10)
因为
=(－7，1，－7)
所以
=(7，－1，7)， =(4，1，2)
所以cosA=
所以∠A=arccos
7.(1)=(1,－3,2), =(2,0,－8)
所以
=1×2+(－3)×0+2×(－8)=－14
所以 =
所以cos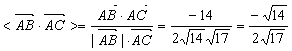
所以sin
所以S△ABC=
(2)设AB边上的高为CD
所以
8.(1)略 (2)45°