高中毕业班摸底测试数学试卷

高中毕业班摸底测试数学试卷

第Ⅰ卷

(选择题共70分)

一、选择题：本题共14个小题，每小题5分，满分70分.

1.　　 两条异面直线a、b，如果a∥平面α，那么必有(　　)
A.b∥α　　　　　　B.b与α相交　　　　 C.bÌα　　　　　　　D.以上都可能

2.　　 (x－1)⁹按x的降幂排列的展开式中，系数最大的是(　　)
A.第4项和第5项　B.第5项　　　　　　C.第5项和第6项　 D.第6项

3.　　 已知集合M＝{xx≠1，x∈R}∪{yy≠2，y∈R}，集合P＝{xx＜1或1＜x＜2或x＞2，x∈R}，则M和P之间的关系是(　　)
A.MP　　　　　 B.MP　　　　　　　C.M＝P　　　　　　D.M∩P＝φ

4.　　 函数y＝sin(2x＋)图象的一条对称轴是直线(　　)
A.x＝　　　　　 B.x＝－　　　　　 C.x＝　　　　　　D.x＝－

5.　　 时两个非零向量，下列命题正确的是(　　)
A.　　　　　　　　　 B.
C.　　　　　 D.

6.　　 如果p是q的充分不必要条件，r是q的必要不充分条件，那么(　　)
A.Øp Þ Ør　　　 B.Øp Ü Ør　　　　　C.Øp ó Ør　　　　D.pór

7.　　 5个男生2个女生排成一排，若女生不能排在两端，且又必须相邻，则不同的排法种数有(　　)
A.480　　　　　　 B.960　　　　　　　 C.720　　　　　　　D.1440

8.　　 动圆x²＋y²－(4m＋2)x－2my＋4m²＋4m＋1＝0的圆心的轨迹方程为(　　)
A.2x－y＋1＝0　　 B.x－2y＋1＝0　　　　C.x－2y－1＝0　　　D.2x＋y－1＝0

9.　　 已知函数f(x)＝，g(x)＝f^－1(－x)，那么g(x)(　　)
A.在(－∞，＋∞)上是增函数　　　　　　 B.在(1，＋∞)上是减函数
C.在(－∞，－1)上是减函数　　　　　　　D.在(－oo，－1)上是增函数

10.　已知数列{－2n＋25}，当它的前n项和最大时，n的值为(　　)
A.10　　　　　　　B.11　　　　　　　　C.12　　　　　　　 D.13

11.　过点P(1，2)引一条直线，使它与A(2，3)和B(4，－5)的距离相等，那么这条直线的方程是(　　)
A.4x＋y－6＝0　　　　　　　　　　　　　B.x＋4y－6＝0
C.3x＋2y－7＝0或4x＋y－6＝0　　　　　 D.2x＋3y－7＝0或x＋4y－6＝0

12.　打靶时，甲每打10次可以中靶8次，乙每打10次可以中靶7次，若两人同时射击一个目标，则他们都中靶的概率是(　　)
A.　　　　　　　B.　　　　　　　　C.　　　　　　　　D.

13.　已知函数y＝f(x)满足f(x)＝f(4－x)(x∈R)，且f(x)在x＞2时为增函数，记a＝f()，b＝f()，c＝f(4)，则a、b、c之间的大小关系为(　　)
A.c＞a＞b　　　　 B.c＞b＞a　　　　　 C.b＞a＞c　　　　　D.a＞c＞b

14.　函数f(x)＝cos²x＋sinxcosx的最大值是(　　)
A.2　　　　　　　 B.　　　　　　　　 C.　　　　　　D.

第Ⅱ卷

(非选择题共80分)

二、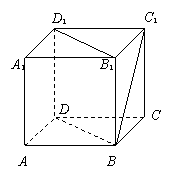空题：本题共4个小题，每小题5分，满分20分.

15.  如图，正方体ABCD－A₁B₁C₁D₁中，直线BC₁与对角面BB₁D₁D所成的角为____________.

16.  不等式组的整数解为_____________________.

17.  若双曲线＝1的实轴长、虚轴长、焦距成等差数列，则这双曲线的离心率是__________________.

18.  教师给出一个函数y＝f(x)，四个学生甲、乙、丙、丁各指出这个函数的一个性质：
甲：对于x∈R，都有f(1＋x)＝f(1－x)；
乙：在(－∞，0]上，函数递减；
丙：在(0，＋∞)上函数递增；
丁：f(0)不是函数的最小值.
如果其中恰有三人说得正确.请写出一个这样的函数______________________.

三、解答题：本大题共5个小题，满分为60分，解答应写出文字说明、证明过程或推演步骤.

19.  (11分)已知三条直线：l₁:2x－2y－1＝0；l₂:3x－5y＋3＝0；l₃:ax－y＋b＝0
(1)求三条直线交于一点的条件；
(2)当三条直线交于一点时，确定a、b的值，使得直线l₃和l₂关于直线l₁对称.

20.  (12分)若函数y＝(a²＋4a－5)x²－4(a－1)x＋3的图象全在x轴的上方，求实数a的取值范围.

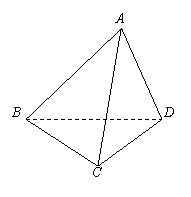
21.  (12分)已知，如图，四面体A－BCD中，AB⊥CD，AC⊥BD.
用向量法求证：AD⊥BC.

22.  (12分)设a∈R，函数f(x)＝ax²＋x－a(－1≤x≤1)
(1)求a的值，使函数f(x)有最大值；
(2)若a≤1，证明：f(x)≤.

23.  (13分)已知双曲线C的方程为x²－y²＋1＝0.
(1)过点P(2，1)且斜率为k的直线与双曲线C交于不同的两点，求实数k的取值范围；
(2)过点P(2，1)是否存在直线l与双曲线交于两点A、B，且P是AB的中点？若存在，试求出直线l的方程；若不存在，说明理由.

高中毕业班摸底测试

数学参考答案

一、DBBDD　BBCDC　CAAC

二、15.30º　　16.(1，0)，(1，－1)，(2，0)，(2，1)，(2，－1)，(3，－1)
　　17.　　  18.y＝(x－1)²等

三、

19．(1)联立方程
解得：　　　　　　　　　　　　　　　　　　　　　　　　　　　 ……2'
代入l₃:＋b＝0，
∴ 11a＋4b＝9　　　　　　　　　　　　　　　　　　　　　　　　　　　 ……4'
(2)∵ 三条直线交于一点，且l₃和l₂关于直线l₁对称
∴ l₃到l₁的角等于l₁到l₂的角.　　　　　　　　　　　　　　　　　　　　　……6'
由因为三条直线斜率都存在，故有
　　　　　　　　　　　　　　　　　　　　　　　　　　　……8，
即　　　　　　　　　　　　　　　　　　　　　　　　　　　　……10'
解得：a＝，从而b＝－　　　　　　　　　　　　　　　　　　　　　　 ……11'

20．若a²＋4a－5＝0，即a＝1或a＝5　　　　　　　　　　　　　　　　　　　 ……1，
当a＝1时，函数为y＝3＞0符合题意；　　　　　　　　　　　　　　　　 ……3'
当a＝5时，函数为y＝24x＋3，其图象不全在x轴上方，舍去.　　　　　　 ……5'
当a≠1且a≠5时，有a²＋4a－5≠0，函数的图象为抛物线.　　　　　　　 ……6'
由题意，有　　　　　　　　　　　　……9'
解得：1＜a＜19　　　　　　　　　　　　　　　　　　　　　　　　　　　……11'
综上所述，a的取值范围是[1，19)　　　　　　　　　　　　　　　　　　　……12'

21．设以空间直角坐标系原点为起点，A、B、C、D为终点的向量分别为
.　　　　　　　　　　　　　　　　　　　　　　　　　　 ……1'
那么　　　　　　　 ……5'
∵ AB⊥CD，∴ ＝0　　　　  ……………………①　　……6'
∵ AC⊥BD，∴ ＝0　　　　  ……………………②　　……7'
①－②得：＝0
∴ ＝0　　　　　　　　　　　　　　　　　　　　　　……10'
即 ＝0　　　　　　　　　　　　　　　　　　　　　　　　　　　 ……11'
∴ AD⊥BC　　　　　　　　　　　　　　　　　　　　　　　　　　　　　……12'

22．(1)当a＝0时，f(x)＝x(－1≤x≤1)的最大值是f(1)＝1，这与题设矛盾.
∴ a≠0，即f(x)是二次函数　　　　　　　　　　　　　　　　　　　　　 ……1'
∵ f(1)＝1，f(－1)＝－1　　　　　　　　　　　　　　　　　　　　　　　……3'
∴ f(x)＝ax²＋x－a(－1≤x≤1)有最大值等价于　　　　　 ……6'
即
解得：a＝－2　　　　　　　　　　　　　　　　　　　　　　　　　　　　……7'
(2)∵ x≤1，a≤1
∴ f(x)＝ax²＋x－a＝a(x²－1)＋x　　　　　　　　　　　　　　　　 ……8'
 ≤a(x²－1)＋x
 ＝ax²－1＋x　　　　　　　　　　　　　　　　　　　　　　　　　 ……9'
 ≤x²－1＋x
 ＝1－x²＋x　　　　　　　　　　　　　　　　　　　　　　　　　　　……10'
＝－(x－　　　　　　　　　　　　　　　　　　　　　　　　　……12'

23．(1)由题意，有
将①代入②，得
(1－k²)x²＋(4k²－2k)x－4k²＋4k＝0　③　　　　　　　　　　　　　　　　 ……2'
由条件，有
　　　　　　　　　　　　　　　 ……4'
解得：k＜0或k＞且k≠±1　　　　　　　　　　　　　　　　　　　　　 ……6'
(2)若P(2，1)为A(x₁，y₁)、B(x₂，y₂)的中点，其中x₁、x₂分别为方程③的两根，
则2＝　　　　　　　　　　　　　　　　　　　　　　　　　　　　　……8'
由韦达定理：x₁＋x₂＝－
∴ －＝2
解得：k＝2　　　　　　　　　　　　　　　　　　　　　　　　　　　　　……11'
此时，1－k≠0，且△＞0　　　　　　　　　　　　　　　　　　　　　　　……12'
故存在题目要求的直线l，其方程为y－1＝2(x－2)
即：2x－y－3＝0.　　　　　　　　　　　　　　　　　　　　　　　　　　……13'

限于篇幅，其他解法不再一一列出，请评卷老师参照以上标准相应给分.

试题提供：四川省成都市新都一中　肖宏

要获取更多的数学资料，请访问我的个人主页：http://cdxh.51.net