高中毕业班数学质量检测(一)
数 学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页.第Ⅱ卷3至4页,另有答题卷4页.满分150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考号、考试科目用铅笔涂写在答题卡上.
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡
皮擦干净后,再选涂其它答案,不能答在试题卷上.
参考公式:
|
|
.
一、选择题:本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有
一项是符合题目要求的.
(1)集合![]() ,
,![]() ,则有
,则有
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(2)![]() 等于
等于
(A)0
(B)1 (C)![]() (D)
(D)![]()
(3)某单位有职工160人,其中业务人员120人,管理人员16人,后勤人员24人. 为了
了解职工的某种情况,要从中抽取一个容量为20的样本. 若要用分层抽样的方法,则抽
取的业务人员,管理人员,后勤人员的人数分别为
(A)7、6、7 (B)15、2、3 (C)10、4、6 (D)17、1、2
(4)已知![]() ,
,![]() ,则
,则![]() 等于
等于
(A)![]() (B)
(B)![]() (C)
(C)
![]() (D)
(D) ![]()
(5)复数![]() 的共轭复数是
的共轭复数是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(6)已知命题![]() ,命题
,命题![]() ,有如下判断:①
,有如下判断:①![]() 或
或![]() 为真;②
为真;② ![]() 或
或![]() 为假;③
为假;③ ![]() 且
且![]() 为真;④
为真;④![]() 为真.其中正确的是
为真.其中正确的是
(A)①② (B)①④ (C)②④ (D)③④
(7)给定两个向量![]() ,
,![]() ,
,![]() ,则x的值等于
,则x的值等于
(A)-3
(B)![]() (C)3 (D)-
(C)3 (D)-![]()
(8)已知函数![]()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(9)设函数f ( x ) 是定义域为R且周期为3的奇函数,若 f ( 1 ) =1 ,f ( 2 ) = a ,则
(A) a =1 (B) a = -1 (C) a = 2 (D) a= -2
(10)从甲地到乙地通话m分钟的电话费由函数![]() 给出,其中m>0, [m]表示大于或等于m的最小整数,如:[3]=3,[3.1]=4, [3.7]=4,则从甲地到乙地通话时间为5.5分钟的电话费为
给出,其中m>0, [m]表示大于或等于m的最小整数,如:[3]=3,[3.1]=4, [3.7]=4,则从甲地到乙地通话时间为5.5分钟的电话费为
(A)3.71元 (B)3.97元 (C) 4.71元 (D) 4.24元
(11)设A、B、C、D是空间不共面的四点,且满足![]() ,
,![]() ,
,![]() 则△BCD是
则△BCD是
(A) 锐角三角形 (B) 直角三角形
(C) 钝角三角形 (D) 以上都有可能
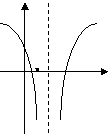
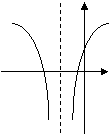 (12)函数
(12)函数![]() (
(![]() ,
,![]() ,
,![]() )的图象可能是
)的图象可能是
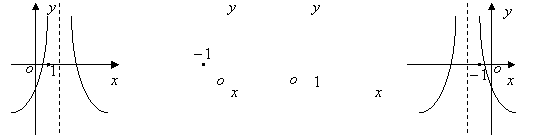 (A)
(B)
(C)
(D)
(A)
(B)
(C)
(D)
第Ⅱ卷(非选择题 共90分)
注意事项:
第Ⅱ卷全部是非选择题,必须在答题区域内,用黑色字迹的钢笔或签字笔作答,不能答在试卷上,否则答案无效.
二、填空题:本大题共4小题,每小题4分,共16分.
(13)若复数![]() ,
,![]() ,则
,则![]() 的模为__________.
的模为__________.
(14)若![]() ,则
,则![]() =
.
=
.
(15)已知函数![]()
![]() ,并且函数
,并且函数![]() 的最小值为
的最小值为![]() ,则实数
,则实数![]() 的取值范围是
.
的取值范围是
.
(16)在某次花样滑冰比赛中,发生裁判受贿事件,竞赛委员会决定将裁判由原来的9名增至14名,但只任取其中7名裁判的评分作为有效分. 若14名裁判中有2人受贿,则有效分中没有受贿裁判的评分的概率是 (结果用数值表示).
三、解答题: 本大题共有6题,满分74分. 解答应写出文字说明、证明过程或演算步骤.
(17)(本小题满分10分)
已知随机变量![]() 的分布列为
的分布列为
|
|
| 0 | 1 | 2 | 3 |
| P | 0.3 | 0.1 |
| 0.3 | 0.2 |
求实数a的值,并求![]() 和
和![]() .
.
(18)(本小题满分12分)
已知函数![]()
![]() ,
,![]() .
.
(Ⅰ)求![]() 的反函数
的反函数![]() ;
;
(Ⅱ)若函数![]() 过点
过点![]() ,则函数
,则函数![]() 过点
过点![]() 吗?为什么?
吗?为什么?
(19)(本小题满分12分)
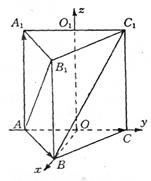
已知正三棱柱ABC—A1B
|
(Ⅰ)求正三棱柱ABC—A1B
(Ⅱ)求异面直线AB1与BC所成角的大小.
(20)(本小题满分12分)
如图,有甲乙两个村庄,甲村位于一直线河岸的岸边A处,乙村与甲村在河的同侧,乙村位于离河岸![]() 元和
元和![]() 元. 现要进行工程费用测算.
元. 现要进行工程费用测算.
(Ⅰ)求出水管总费用关于水厂C到D的距离的函数
 关系式;
关系式;
(Ⅱ)问自来水厂C建在何处,才能使水管总费用最
省?
(21)(本小题满分14分)
在以O为原点的直角坐标系中,点A(3,-1)为![]() 的直角顶点. 已知AB=2OA,且点B的纵坐标大于零.
的直角顶点. 已知AB=2OA,且点B的纵坐标大于零.
(Ⅰ)求向量![]() 的坐标;
的坐标;
(Ⅱ)是否存在实数a,使二次函数![]() 的图像上总有关于直线OB对称的两个不同的点?若不存在,说明理由;若存在,求a的取值范围.
的图像上总有关于直线OB对称的两个不同的点?若不存在,说明理由;若存在,求a的取值范围.
(22)(本小题满分14分)
若数列{![]() }的通项
}的通项![]() ,设数列{
,设数列{![]() }的通项
}的通项![]() ,又记
,又记![]() 是数列{
是数列{![]() }
}
的前n项的积.
(Ⅰ)求![]() ,
,![]() ,
,![]() 的值;
的值;
(Ⅱ)试比较![]() 与
与![]() 的大小,并证明你的结论.
的大小,并证明你的结论.
高中毕业班质量检测(一)
数学 参考答案
一、B C B C D B A D B D A D
二、填空题:
13、![]() 14、
14、![]() 15、
15、![]() 16、
16、![]()
三、解答题
17.[解]
由![]()
得![]() ………………………………………………..3分
………………………………………………..3分
![]() ………..6分
………..6分
![]() ……………………………………………………………………….10分
……………………………………………………………………….10分
18.[解](Ⅰ)由![]() …………………………………3分
…………………………………3分
![]() -----------------------------------------------------------4分
-----------------------------------------------------------4分
![]() ……………………………………5分
……………………………………5分
![]()
![]() …………6分
…………6分
(Ⅱ)
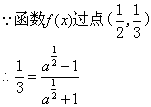
![]() …………………………………9分
…………………………………9分
![]()
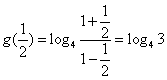
![]() …………………………………12分
…………………………………12分
19.[解](Ⅰ)设正三棱柱的高为h,由AB=2及正三棱柱的性质知B
![]()
![]() 又
又![]() , ……………2分
, ……………2分
即![]()
![]() ,则正三棱柱的侧棱长为
,则正三棱柱的侧棱长为![]() .……4分
.……4分
(Ⅱ)![]()
![]() …………………………………7分
…………………………………7分
![]() ,………………………………10分
,………………………………10分
而![]() ……………………………………11分
……………………………………11分
∴异面直线AB1与BC所成角的余弦值为![]()
![]() …………………12分
…………………12分
20.[解](1)设C到D的距离为xkm,
![]() BD=
BD=
![]() BC=
BC=![]() ………………………2分
………………………2分
又设总的水管费用为y元,依题意有:
![]()
![]()
即![]()
![]() 为所求函数关系式
为所求函数关系式
…………………………………………………………………………………………..….6分
(2)![]()
![]()
![]()
![]()
![]()
![]() …………………………………8分
…………………………………8分
令![]() …………………………………10分
…………………………………10分
在(0,50)上,y只有一个极值点。根据实际意义,函数在x=30(km)处取得最小值,此时AC=![]() =20(km)
=20(km)
![]() …………….12分
…………….12分
21.[解](1)设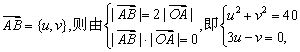 ………………2分
………………2分
得
![]() ……………………5分
……………………5分
所以v-1>0,得v=6,故![]() =(2,6). …………………………………6分
=(2,6). …………………………………6分
(2)∵![]() =(2,6),又A(4,-3),∴B点的坐标为(5,5)……………………8分
=(2,6),又A(4,-3),∴B点的坐标为(5,5)……………………8分
则直线OB的方程为y=x.
设P (x0,y0) 关于直线OB:y=x对称点为Q (y0, x0) ,
若点P、Q在二次函数![]() 图像上,则
图像上,则
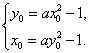 得
得![]() ……………………………10分
……………………………10分
![]() ,
,![]()
将![]() 代入
代入![]() 中得
中得
![]() 由题意得
………………………………12分
由题意得
………………………………12分
![]()
![]() ………………………………14分
………………………………14分
故当![]() 时,抛物线y=ax2-1上总有关于直线OB对称的两点.
时,抛物线y=ax2-1上总有关于直线OB对称的两点.
22.[解]
(1)![]()
![]()
![]()
![]() …………………………………2分
…………………………………2分
![]() ……………………3分
……………………3分
![]() ………………………4分
………………………4分
(2)由(1)中可猜想得Tn>![]() ;…………………………………6分
;…………………………………6分
只须证明对于n∈N, ![]() 成立
成立
设n=1时,左=1+1=2,右=![]() ,
,
∵2>![]() ,故原不等式成立; …………………………………7分
,故原不等式成立; …………………………………7分
假设n=k(k≥1)时,原不等式成立,即![]() ,
,
当n=k+1时,不等式左边为
![]()
![]()
不等式的右边为![]() ,
,
只须得出![]() >
>![]() ,…………………………………10分
,…………………………………10分
事实上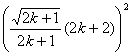 -
-![]()
=![]() =
=![]() >0,……………………………12分
>0,……………………………12分
故![]() >
>![]() 成立,从而
成立,从而
![]() >
>![]() 。
。
即n=k+1时不等式也成立,
∴对于n∈N,则有![]() 成立。
成立。
…………………………………14分