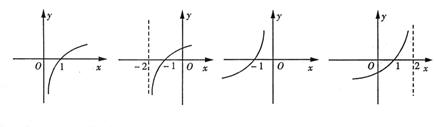高中毕业班数学质量检查
(理科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题),全卷满分150分,考试时间120分钟.
第Ⅰ卷(选择题 共60分)
参考公式:
如果事件A、B互斥,那么P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么P(A·B)=P(A)·P(B)
如果事件A在一次试验中发生了概率是P,那么它在n次独立重复试验中恰好发生k次的概率![]() .
.
球的表面积公式![]() ,其中R表示球的半径.
,其中R表示球的半径.
球的体积公式![]() ,其中R表示球的半径.
,其中R表示球的半径.
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设p、q是两个命题,则“复合命题p或q为真,p且q为假”的充要条件是 ( )
A.p、q中至少有一个为真 B.p、q中至少有一个为假
C.p、q中中有且只有一个为真 D.p为真,q为假
2.已知复数![]() ( )
( )
A.![]() B.2 C.2
B.2 C.2![]() D.8
D.8
3.已知a、b、c是三条互不重合的直线,α、β是两个不重合的平面,给出四个命题:
①![]() ②a、
②a、![]() ③
③![]() ④
④![]() .其中正确命题的个数是 ( )
.其中正确命题的个数是 ( )
A.1个 B.2个 C.3个 D.4个
4.已知等差数列![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.定义在R上的偶函数![]() 的x的集合为 ( )
的x的集合为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
|
A.![]() B.1
B.1
C.6 D.3
7.已知函数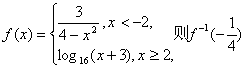 的值等于 ( )
的值等于 ( )
A.![]() B.
B.![]() C.4 D.-4
C.4 D.-4
8.若半径为R的球与正三棱柱的各个面都相切,则球与正三棱柱的体积比为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9.如果以原点为圆心的圆经过双曲线![]() 的焦点,而且被该双曲线的右准线分成弧长为2:1的两段圆弧,那么该双曲线的离心率e等于 ( )
的焦点,而且被该双曲线的右准线分成弧长为2:1的两段圆弧,那么该双曲线的离心率e等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
|
A.![]() B.
B.![]()
|
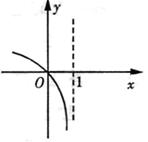
11.若函数![]() 的图象如右图所示,则
的图象如右图所示,则
函数![]() 的图象大致为( )
的图象大致为( )
|
A B C D
12.已知函数![]() 有以下四个函数:①
有以下四个函数:①![]() ②
②![]() ③
③![]()
④![]()
其中满足f (x)所有条件的函数序号为 ( )
A.①② B.②③ C.②④ D.①④
第Ⅱ卷(非选择题 共90分)
|
13.![]() 展开式中的常数项为
.
展开式中的常数项为
.
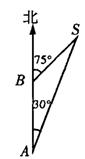
14.如图,一艘船上午9:30在A处测得灯塔S在它的北偏东30°处,之后它继续沿正北方向匀速航行,上午10:00到达B处,此时又测得灯塔S在它的北偏东75°处,且与它相距8![]() n mile.此船的航速是
n mile/h.
n mile.此船的航速是
n mile/h.
|
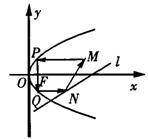
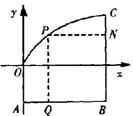
16.如图,从点![]() 发出的光线沿平行于抛物线
发出的光线沿平行于抛物线![]() 的轴的方向射向此抛物线上的点P,反射后经焦点F又射向抛物线上的点Q,再反射后沿平行于抛物线的轴的方向射向直线
的轴的方向射向此抛物线上的点P,反射后经焦点F又射向抛物线上的点Q,再反射后沿平行于抛物线的轴的方向射向直线![]() 再反射后又射回点M,则
再反射后又射回点M,则
x0= .
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
![]()
18.(本小题满分12分)
抛掷两个骰子,当至少有一个2点或3点出现时,就说这次试验成功.
(Ⅰ)求一次试验中成功的概率;
(Ⅱ)求在4次试验中成功次数ξ的概率分布列及ξ的数学期望与方差.
19.(本小题满分12分)
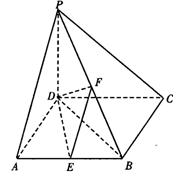
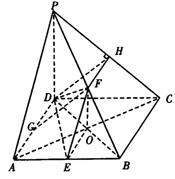
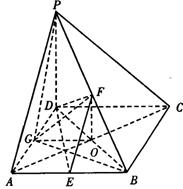
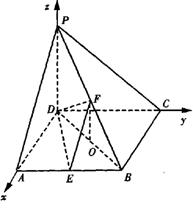
如图,在四棱锥P—ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E、F分别是AB、PB的中点.
(Ⅰ)求证:EF⊥CD;
(Ⅱ)在平面PAD内求一点G,使GF⊥平面PCB,并证明你的结论;
|
20.(本小题满分12分)
|
21.(本小题满分12分)
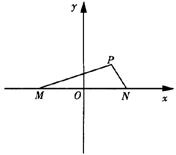
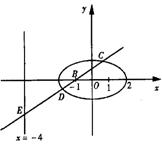
如图,已知在坐标平面内,M、N是x轴上关于原点O对称的两点,P是上半平面内一点,△PMN的面积为![]()
![]()
(Ⅰ)求以M、N为焦点且过点P的椭圆方程;
(Ⅱ)过点B(-1,0)的直线l交椭圆于C、D两点,交直线x=-4于点E,点B、E分
|
22.(本小题满分14分)
已知一列非零向![]()
(Ⅰ)证明:![]() 是等比数列;
是等比数列;
(Ⅱ)求向量![]()
(Ⅲ)设![]() 一列,记为
一列,记为![]() 为坐标原点,求点列{Bn}的极限点B的坐标.
为坐标原点,求点列{Bn}的极限点B的坐标.
(注:若点Bn坐标为![]() 的极限点.)
的极限点.)
高中毕业班质量检查
数 学(理科)参考答案及评分标准
说明:
一、本解答指出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制定相应的评分细则.
二、对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应给分数的一半;如果后继部分的解答有较严重的错误,就不再给分.
三、解答右端所注分数,表示考生正确做到这一步应得的累加分数.
四、只给整数分数,选择题和填空题不给中间分.
一、选择题:本题考查基本知识和基本运算,每小题5分,满分60分.
1.C 2.C 3.B 4.D 5.D 6.B 7.D 8.B 9.D 10.A 11.A 12.B
二、填空题:本题考查基本知识和基本运算,每小题4分,满分16分.
13.![]() 14.32 15.16 16.6
14.32 15.16 16.6
三、解答题:
17.本小题主要考查三角函数的基础知识,以及换元配方法,分类讨论思想方法和运算能力,满分12分.
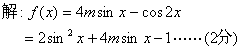
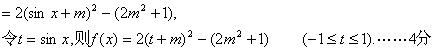
①![]()
![]() ……7分
……7分
②![]()
![]()
综上,![]() ……12分
……12分
18.本小题主要考查概率及其基础知识和运算能力,满分12分.
解(Ⅰ)一次实验中,设事件A表示“试验成功”,则
![]() ……4分
……4分
(Ⅱ)依题意得:![]()
| ξ | 0 | 1 | 2 | 3 | 4 |
| P |
|
|
|
|
|
……………………………………………………………………………………8分
![]() ………………12分
………………12分
19.本小题主要考查空间线面关系,考查空间想象能力和推理论证能力,满分12分.
|
(Ⅰ)(证法一)

(证法二)取BD的中点O,连结FO、OE.

(Ⅱ)答:G是AD的中点.…………5分
(方法一)取PC的中点H,连结DH.

|
![]() ≌
≌![]()

(Ⅲ)设B到平面DEF的距离为d.

解法二:
|
D(0,0,0)、A(a,0,0)、B(a,a,0)、C(0,a,0)
![]() 、
、![]() 、
、![]() ……2分
……2分
(Ⅰ)![]()
![]() ……4分
……4分
(Ⅱ)![]()

(Ⅲ)设平面DEF的法向量为![]()

|
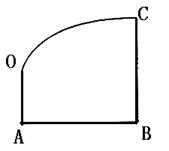
解法一:以O为原点,OA所在直线为y轴建
立直角坐标系如图,依题意可设抛物线方程为
![]()
![]() ,
,
故曲线段OC的方程为![]() ………………3分
………………3分
设![]() 是曲线段OC上的任意一点,
是曲线段OC上的任意一点,
则在矩形PQBN中,![]() ,………………5分
,………………5分
工业区面积![]() ,…………6分
,…………6分
![]()
即:![]() ………………7分
………………7分
当![]() 的增函数;………………8分
的增函数;………………8分
当![]() 的减函数;………………9分
的减函数;………………9分
![]() 时,S取到极大值,此时
时,S取到极大值,此时![]()
![]() ……………………10分
……………………10分
![]() ……………………11分
……………………11分
答:把工业园区规划成长为![]() ,宽为
,宽为![]() 的矩形时,工业园区的面积最大,
的矩形时,工业园区的面积最大,
最大面积约为9.5km2.…………………………12分
解法二:由解法一得:曲线段OC的方程为![]() …………3分
…………3分
设![]() 是曲线段OC上的任意一点,
是曲线段OC上的任意一点,
则在矩形PQBN中,![]() ………………5分
………………5分
∴工业区面积![]() …………6分
…………6分
![]() .
.
![]() ……………………7分
……………………7分
当![]() 的增函灵敏;……………………8分
的增函灵敏;……………………8分
当![]() 时,
时,![]() 的减函数,………………9分
的减函数,………………9分
![]() 时,S取到极大值,此时
时,S取到极大值,此时![]() ,
,
![]() ………………10分
………………10分
![]() ……………………11分
……………………11分
答:把工业园区规划成长为![]() 的矩形时,工业园区的面积最大,最大面
的矩形时,工业园区的面积最大,最大面
积约为![]() .…………………………12分
.…………………………12分
21.本小题主要考查平面向量的概念、直线与椭圆的方程性质以及综合运用所学知识分析、
解决问题的能力. 满分12分.
解:(1)设![]()
则![]()
![]() ① 又
① 又![]() ②…………2分
②…………2分
![]() 由已知
由已知![]()
即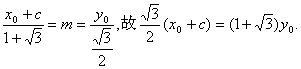 ③
③
将①②代入③,![]()
![]()
![]()
![]() …………………………4分
…………………………4分
设椭圆方程为![]() 在椭圆上,
在椭圆上,
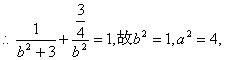
∴椭圆方程为:![]() ……………………6分
……………………6分
|
不合题意.
②当![]() 的斜率存在时,设
的斜率存在时,设![]() 方程为
方程为![]() ,
,
代入椭圆方程![]()
化简得:![]() ……8分
……8分
设点![]() 、
、![]() ,则:
,则:
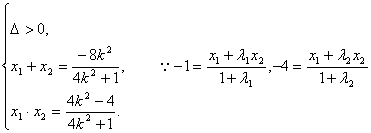 ,
,
![]() ………10分
………10分
![]()
而![]()
![]() ,
, ![]() …………12分
…………12分
22.本小题主要考查数列、平面向量、极限等基础知识,考查综合应用数学知识,直觉猜想,
归纳推理及运算能力. 满分14分.
解:(1)![]()
![]() ………………2分
………………2分
首项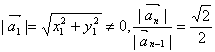 为常数,
为常数, ![]() 是等比数列.………3分
是等比数列.………3分
(2)![]()
![]() ,…………………………5分
,…………………………5分
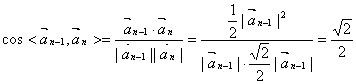 ,
,
![]() 的夹角为
的夹角为![]() ………………7分
………………7分
(3)![]()
![]()
![]()
![]() … ……8分
… ……8分
一般地,![]()
用数学归纳法易证![]() 成立.………………10分
成立.………………10分
![]() ……………………11分
……………………11分
设![]()
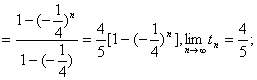
![]()
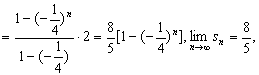
∴极限点B的坐标为![]() ………………………………14分
………………………………14分