高三数学统练试卷
一、选择题:(共12题,每题5分,共60分)
1.设集合![]() ,
,![]() ,则
,则![]() ( )
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2.当![]() 时,下列不等式中正确的是( )
时,下列不等式中正确的是( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
3.给出四个命题:
(1)若平面![]() ,则“点P在
,则“点P在![]() 上”是“点P为
上”是“点P为![]() 的公共点”的充要条件;
的公共点”的充要条件;
(2)“a,b是异面直线”指的是“![]() ”;
”;
(3)分别与两异面直线a,b都相交的两条直线必是异面直线;
(4)如果一条直线与一个平面的斜线垂直,则它必然与斜线在该平面内的射影垂直;
其中正确命题的个数为( )
(A)0 (B)1 (C)2 (D)3
4.(理)已知![]() ,
,![]() ,且
,且![]() ,则下列不等式正确的是 ( )
,则下列不等式正确的是 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(文)不等式![]() 的解集是( )
的解集是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
5.设有两个命题:(1)关于![]() 的不等式
的不等式![]() 对一切
对一切![]() 恒成立;(2)函数
恒成立;(2)函数![]() 是减函数。若这两个命题中有且只有一个是真命题,则实数
是减函数。若这两个命题中有且只有一个是真命题,则实数![]() 的取值范围是( )
的取值范围是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
6.有如下三个命题:
甲:相交两条直线![]() 都在平面
都在平面![]() 内,并且都不在平面
内,并且都不在平面![]() 内
内
乙:![]() 之中至少有一条与
之中至少有一条与![]() 相交
相交
丙:![]() 与
与![]() 相交
相交
当甲成立时,( )
(A)乙是丙的充分而不必要条件 (B)乙是丙的必要而不充分条件
(C)乙是丙的充分且必要条件 (D)乙既不是丙的充分条件,也不是丙的必要条件
7.椭圆C与椭圆![]() 关于直线
关于直线![]() 对称,则椭圆C的方程为( )
对称,则椭圆C的方程为( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
8.已知不等式![]() 的解集为(-3,0)那么a的值是( )
的解集为(-3,0)那么a的值是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)3
(D)3
9.设![]() 为三条不同的直线,
为三条不同的直线,![]() 为三个不同的平面,下列四个命题中真命题的个数是
为三个不同的平面,下列四个命题中真命题的个数是
(1)若![]() ,则
,则![]() ;(2)若
;(2)若![]() ,则
,则![]() 或
或![]() ;
;
(3)若![]() ,则
,则![]() ;(4)若
;(4)若![]() ,则
,则![]() ;
;
(A)1个 (B)2个 (C)3个 (D)4个
10.已知点M到A(0,1),B(2,a)及x轴的距离都相等,若满足条件的点M只有一个,则![]() 的值为( )
的值为( )
(A)0或2 (B)0或1 (C)-1或1 (D)1或2
11.对于抛物线y2=4x上任意一点Q,点P(a,0)都满足∣PQ∣![]() ∣
∣![]() ∣,则a的取值范围是( )
∣,则a的取值范围是( )
(A)![]() (B)
(B)![]() (C)[0,2] (D)(0,2)
(C)[0,2] (D)(0,2)
12.已知![]() ,则
,则![]() 的最小值是( )
的最小值是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
二、填空题:(共8题,每题5分,共40分)
13.在正方体![]() 中,M,N分别是
中,M,N分别是![]() 和
和![]() 的中点,若θ为直线
的中点,若θ为直线![]() 与
与![]() 所成的角,则cosθ=____。
所成的角,则cosθ=____。
14.若关于x 的不等式![]() 在R上恒成立,则
在R上恒成立,则![]() 的最大值是______。
的最大值是______。
15.若![]() ,则实数a的取值范围是______。
,则实数a的取值范围是______。
16.直线![]() 被圆
被圆![]() 截得的弦长为8,则
截得的弦长为8,则![]() 的最大值是______。
的最大值是______。
17.已知椭圆![]() 与圆
与圆![]() 有公共点,则a的最大值和最小值分别为______。
有公共点,则a的最大值和最小值分别为______。
18.已知![]() ,则
,则![]() 的最小值是______。
的最小值是______。
19.下面四个命题:
(1) 经过两两相交的三条直线确定一个平面;
(2) 经过平面外一点,有且只有一个平面与这个平面垂直;
(3) 若![]() 是异面直线,则一定存在平面
是异面直线,则一定存在平面![]() 与直线
与直线![]() 所成的角相等;
所成的角相等;
(4) 平面![]() 相交,直线
相交,直线![]() ,则
,则![]() 内不一定存在直线与
内不一定存在直线与![]() 平行,但必存在直线与
平行,但必存在直线与![]() 垂直;
垂直;
(5) 两个平面互相垂直,过其中一个平面内的一点作它们交线的垂线,则此垂线垂直于另一个平面;
其中真命题的序号为______。
20.要挖一个面积为800![]() 的矩形养鱼池,并在四周围绕鱼塘修出宽分别为1
的矩形养鱼池,并在四周围绕鱼塘修出宽分别为1![]() 和2
和2![]() 的路,对边的路宽相等,当为修此鱼池而占地的总面积最小时,鱼池的长和宽分别为______
的路,对边的路宽相等,当为修此鱼池而占地的总面积最小时,鱼池的长和宽分别为______![]() 。
。
三、解答题:(共4个题,总分50分)
21.(本题12分)解关于x的不等式:![]()
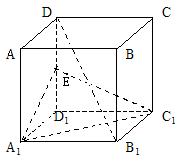
22.(本题12分)正方体![]() 中,点E是
中,点E是![]() 的中点,如图,
的中点,如图,
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)求证:![]() 不垂直于平面
不垂直于平面![]() 。
。

23.(本题13分)函数![]() ,
,![]()
1)m=1时,解不等式![]() ;
;
2)若对于满足![]() 的一切实数m,都有
的一切实数m,都有![]() ,求x的范围。
,求x的范围。
24.(本题13分)抛物线![]() ,过动点
,过动点![]() 且斜率为1的直线
且斜率为1的直线![]() 与该抛物线交于不同两点
与该抛物线交于不同两点
A、B,AB![]() 2p,
2p,
1)求![]() 的取值范围;
的取值范围;
2)若线段AB的垂直平分线交x轴于N点,求⊿NAB面积的最大值。
高三数学统练试卷答案
行政班_________ 分组教学班_________ 姓名_________ 得分_________
一、选择题:(共12题,每题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 答案 | A | D | B | B | D | C |
| 题号 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | B | A | B | B | A |
二、填空题:(共8题,每题5分,共40分)
13.__![]() __ 14. 1 15.__
__ 14. 1 15.__![]() __ 16.__
__ 16.__![]() __
__
17. 6,-6 18.__5+2![]() __ 19. (3) (4) 20. 40,20
__ 19. (3) (4) 20. 40,20
三、解答题:(共4个题,总分50分)
21.(本题12分)解关于x的不等式:![]()
解:设![]() ,不等式可化为
,不等式可化为![]()
![]() ,
,![]() ,即
,即![]()
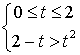 或
或
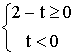
解得![]() 或
或![]() ,
,![]() 即
即![]()
![]() 时,
时,![]() ;
;![]() 时,
时,![]() 。
。
22.(本题12分)正方体![]() 中,点E是
中,点E是![]() 的中点,如图,
的中点,如图,
(1) 求证:![]() ,
,
(2) 求证:![]() ,
,
(3) 求证:![]() 不垂直于平面
不垂直于平面![]() 。
。
解答:略。
23.(本题13分)函数![]() ,
,![]()
1)m=1时,解不等式![]() ;
;
2)若对于满足![]() 的一切实数m,都有
的一切实数m,都有![]() ,求x的范围。
,求x的范围。
解:1)![]() 时,
时,![]() ,解得
,解得![]() ,
,
2)![]() 对任意
对任意![]() 均成立,由图可知,
均成立,由图可知,
所求范围是夹在![]() 时直线与曲线的两交点之间的点所对应的
时直线与曲线的两交点之间的点所对应的![]() 的取值范围。
的取值范围。
![]() 时,令
时,令![]() ,得
,得![]()
![]() 时,令
时,令![]() ,得
,得![]()
则所求范围是![]() 。
。
24.(本题13分)抛物线![]() ,过动点
,过动点![]() 且斜率为1的直线
且斜率为1的直线![]() 与该抛物线交于不同两点
与该抛物线交于不同两点
A、B,AB![]() 2p,
2p,
1)求![]() 的取值范围;
的取值范围;
2)若线段AB的垂直平分线交x轴于N点,求⊿NAB面积的最大值。
解:1)设![]() 与
与![]() 联立得
联立得![]()
即![]()
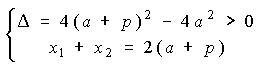
![]()
![]() ,解得
,解得![]()
又由![]() ,得
,得![]()
∴ ![]() 的取值范围是
的取值范围是![]() 。
。
2)线段AB的中点为![]() ,
,
线段AB的垂直平分线是![]() ,即
,即![]()
令![]() ,则
,则![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]() 。
。