高三数学统一考试
数学(理工类)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。共150分。考试时间为120分种。
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分;共60分。在每小题给出的四个选项中,只有
一项是符合题目要求的。
1.函数![]() 定义域是 ( )
定义域是 ( )
A.(1,![]() B.(0,
B.(0,![]() C.[1,
C.[1,![]() D.[1,
D.[1,![]()
2.已知![]() ,则 ( )
,则 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.已知△ABC中,点D在BC边上,且![]() 则
则![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.-3 D.0
C.-3 D.0
4.在等差数列{![]() }中,若
}中,若![]() 则S13的值是 ( )
则S13的值是 ( )
A.54 B.168 C.117 D.218
5.下表是某工厂产品的销售价格表
| 一次购买件数 | 1~10件 | 11~50件 | 51~100件 | 101~300件 | 300件以上 |
| 每件价格(单位:元) | 37 | 32 | 30 | 27 | 25 |
某人有现金2900元,最多可购买该产品的件数为 ( )
A.108 B.107 C.97 D.96
6.已知直线![]() ( )
( )
A.![]() 的充要条件 B.
的充要条件 B.![]() 的必要不充分条件
的必要不充分条件
C.![]() 的充要条件 D.
的充要条件 D.![]() 的充分不必要条件
的充分不必要条件
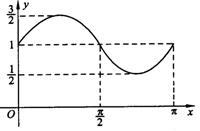
|
则它的解析式是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.若直线![]() 与线段AB有交点,其中A(-2,3),B(3,2),则
与线段AB有交点,其中A(-2,3),B(3,2),则![]() 的取值范
的取值范
围是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9.若![]() 的值为 ( )
的值为 ( )
A.-1 B.![]() C.
C.![]() D.
D.![]()
10.把直线![]() 按向量
按向量![]() 平移后,所得直线与圆
平移后,所得直线与圆![]() 相
相
切,则实数![]() 的值为 ( )
的值为 ( )
A.39 B.13 C.-21 D.-39
11.平面内有10条直线,其中任意两条都相交,任意三条都不过同一点,它们将平面分割
成![]() 个部分,则
个部分,则![]() 的值为 ( )
的值为 ( )
A.54 B.55 C.56 D.92
12.定义在R上的偶函数![]() 满足
满足![]() ,且在[-3,-2]上是减函数,
,且在[-3,-2]上是减函数,![]() 是
是
钝角三角形的两个锐角,则![]() 与
与![]() 的大小关系是 ( )
的大小关系是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题4分;共16分. 把答案填在题中横线上.
13.函数![]() )的图象与其反函数图象交点坐标为
.
)的图象与其反函数图象交点坐标为
.
14.已知![]() 与
与![]() 的夹角为60°,则
的夹角为60°,则![]() 与
与![]() -
-![]() 的夹角余弦为
的夹角余弦为
.,
15.定义符号函数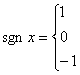
![]() ,则不等式
,则不等式![]() 的解集是
.
的解集是
.
16.若z=![]() 满足约束条件
满足约束条件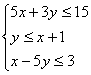 ,则Z的最大值和最小值分别为
,则Z的最大值和最小值分别为
.
三、解答题:本大题6小题. 共74分.解答应写出文字说明、证明过程或推演步骤.
17.(本小题满分12分)
已知函数![]()
(1)求![]() 的最大值有相庆的
的最大值有相庆的![]() 的取集体合;
的取集体合;
(2)该函数的图象经过怎样的平移和伸变换可以得到![]() 的图象.
的图象.
18.(本小题满分12分)
等差数列{![]() }的前
}的前![]() 项和为Sn,等比数列{
项和为Sn,等比数列{![]() 的前
的前![]() 项和为
项和为![]() ,其公比为
,其公比为![]() ,若它们满足
,若它们满足![]()
(1)证明数列{![]() }不是常数列;
}不是常数列;
(2)比较S4和T4的大小.
19.(本小题满分12分)
已知函数![]()
(1)求![]() 的定义域;
的定义域;
(2)判断![]() 的奇偶性,并予以证明;
的奇偶性,并予以证明;
(3)求使![]() 的
的![]() 的取值范围.
的取值范围.
20.(本小题满分12分)
已知函数![]() 的图象与函数
的图象与函数![]() 的图象关于点A(0,1)对称.
的图象关于点A(0,1)对称.
(1)求![]() 的解析式;
的解析式;
(2)若![]() 且
且![]() 在
在![]() 上为减函数,求实数
上为减函数,求实数![]() 的取值范围.
的取值范围.
21.(本小题满分12分)
在平行四边形ABCD中,A(1,1),![]() ,点M是线段AB的中点,线段CM与BD交于点P.
,点M是线段AB的中点,线段CM与BD交于点P.
(1)若![]() ,求点C的坐标;
,求点C的坐标;
(2)当![]() 时,求点P的轨迹.
时,求点P的轨迹.
22.(本小题满分14分)
已知二次函数![]() 满足以下条件:
满足以下条件:
①![]() ;
;
②![]() ;
;
③对任意实数![]() 恒成立.
恒成立.
(1)求![]() 的表达式;
的表达式;
(2)数列![]() 、
、![]() ,若对任意的实数
,若对任意的实数![]() 都满足
都满足![]()
其中![]() 是定义在实数集R上的一个函数.求数
是定义在实数集R上的一个函数.求数![]() 与
与![]() 的通项公式;
的通项公式;
(3)设圆![]() ,若圆
,若圆![]() 现圆
现圆![]() 外切,
外切,![]() 是各项都是正
是各项都是正
数且公比为![]() 的等比数列.求
的等比数列.求![]()
高三(理工类)数学试题参考答案及评分标准
一、1.C 2.D 3.D 4.C 5.B 6.B 7.C 8.C 9.D 10.A 11.C 12.B
二、13.(0,0),(1,1) 14.![]() 15.
15.![]() 16.17和-11
16.17和-11
三、17.解:![]() ……4分 (1)
……4分 (1)![]() ……8分
……8分
(2)把![]() 图象向右平移
图象向右平移![]() ,再把每个点的纵坐村为原来的
,再把每个点的纵坐村为原来的![]() ,横坐标
,横坐标
不变.然后再把每个点的横坐标变为原来的![]() ,纵坐标不变,即可得到
,纵坐标不变,即可得到![]() 的
的
图象……12分
18.(1)证明:![]() 又
又![]() ……1分
……1分
![]() 即
即![]() ……3分
……3分
![]() 数列
数列![]() 不是常数列……4分
不是常数列……4分
(2)解:![]() ……6分
……6分
|
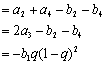
又![]() ……10分
……10分 ![]() ……12分
……12分
19.解:(1)由对数函数定义知![]() ……1分 解得
……1分 解得![]() ……3分
……3分
故函数![]() 的定义域为
的定义域为![]() ……4分
……4分
(2)![]() ……5分
……5分
![]() ……6分
……6分
=-![]()
由奇函数定义知![]() 为奇函数……7分
为奇函数……7分
(3)当![]() 时 由对数函数单调性知
时 由对数函数单调性知![]() ……8分
……8分
结合![]() 解这个不等式得
解这个不等式得![]() ……10分
……10分
当![]() 时 由对数函数单调性知
时 由对数函数单调性知![]() ……11分
……11分
结合![]() 解这个不等式得
解这个不等式得![]() ……12分
……12分
20.解:(1)设![]() 是
是![]() 图象上任意点……1分
图象上任意点……1分
则P关于A(0,1)的对称点![]() ……3分
……3分
由题意知![]() 在
在![]() 的图象上
的图象上
![]() ……5分
……5分
即![]() ……6分
……6分
(2)![]() =7分
=7分
![]() 上为减函数
上为减函数 ![]() 上恒成立……9分
上恒成立……9分
即![]() 上恒成立……11分
上恒成立……11分 ![]() ……12分
……12分
21.解:(1)设点C坐标为(![]() ……1分
……1分
又![]() ……3分
……3分
即![]() ……4分
……4分
![]() 即点C(0,6)……5分
即点C(0,6)……5分
(2)解一:设![]() ,则
,则
![]() ……6分
……6分
|
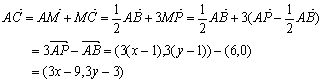
![]()
![]() ABCD为菱形……9分
ABCD为菱形……9分
![]()
![]()
![]() ……11分
……11分
故点P的轨迹是以(5,1)为圆心,2为半圆去掉与直线![]() 的两个交点……12分
的两个交点……12分
解法二:![]()
![]() D的轨迹方程为
D的轨迹方程为![]() ……7分
……7分
![]() M为AB中点
M为AB中点 ![]() 的比为
的比为![]()
设![]() ……9分
……9分
![]() 的轨迹方程
的轨迹方程 ![]()
整理得![]() ……11分
……11分
故点P的轨迹是以(5,1)为圆心,2为半径的圆去掉与直线![]() 的两个交
的两个交
点……12分
22.解:(1)由条件得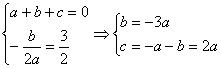 ……2分
……2分
由![]() 恒成立
恒成立
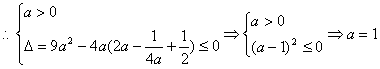 ……4分
……4分
![]() ……5分
……5分
(2)![]() 恒成立
恒成立
令![]() ……7分
……7分
![]() ……10分
……10分
(3)![]()
![]() 相外切
相外切 ![]() ……11分
……11分
而![]()
![]() 即
即![]() ……13分
……13分
![]() ……14分
……14分