高三数学月考
(第Ⅰ卷)
一、选择题(本题每小题5分,共60分)
1.已知集合![]() ,集合
,集合![]() ,则
,则![]() 是
是
A.
![]() B.
B. ![]() C.
C.
![]() D.
D.
![]()
2.(文科做)曲线y=x3+x-2 在点P0处的切线平行于直线y=4x-1,则点P0点的坐标是
A.(0,1) B.(1,0) C.(-1,0) D.(1,4)
(理科做)函数y=2x3-3x2-12x+5在[0,3]上的最大值与最小值分别是
A.5 , -15 B.5 , 4 C.-4 , -15 D.5 , -16
3.函数![]() 是单调函数的充要条件是
是单调函数的充要条件是
![]()
![]()
![]()
![]()
4.设![]() ,若
,若![]() 、
、![]() 且
且![]() ,则下列不等式必定成立的是
,则下列不等式必定成立的是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.设函数f (x)=ax2+bx+c对任意实数t都有f (2+t)= f (2-t)成立,在函数值f (-1),f (1),f (2),f (5)中的最小的一个不可能是
A.f (-1) B.f (1) C.f (2) D.f (5)
6.设函数![]() 表示
表示![]() 除以3的余数,对
除以3的余数,对![]() 都有
都有
A.
![]() B.
B.
![]()
C.
![]() D.
D.
![]()
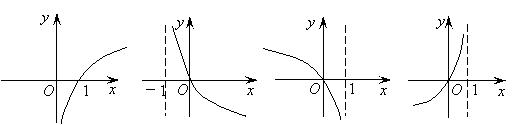 7.函数
7.函数![]() 的图象是
的图象是
A. B. C. D.
8.(文科做)![]()
(A)0 (B)![]() (C)1 (D)2
(C)1 (D)2
(理科做)用数学归纳法证明:x2n-y2n (n∈Z+)能被x+y 整除的第二步是:假设n=k(k∈Z+)时,x2k-y2k 能被x+y 整除,证当n=k+1时,x2(k+1)-y2(k+1)也能被x+y 整除。则在证明过程中,x2(k+1)-y2(k+1) 的合理变形是
(A)( xk+1+yk+1)(xk+1-yk+1) (B) x2k(x2 +y2)-y2 (x2k+y2k)
(C) x2(x2k-y2k)+y2k (x2 -y2) (D) x2(x2k+y2k)-y2k (x2 +y2)
9.函数f(x)=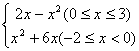 的值域是
的值域是
(A)R (B)[-9,+![]() ] (C)[-8,1] (D)[-9,1]
] (C)[-8,1] (D)[-9,1]
10.由等式![]()
![]() 定义
定义![]() ,则
,则![]() 等于
等于
A.![]() B.
B.![]()
C.![]() D.
D.![]()
11.a1、b1、c1、a2、b2、c2均为非零实数,不等式a1x2+b1x+c1>0和a2x2+b2x+c2>0的解集分别为集合M和N,那么“![]() ”是“M=N”的
”是“M=N”的
A.充分非必要条件. B.必要非充分条件.
C.充要条件 D.既非充分又非必要条件.
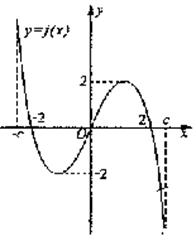
|
其图象如图所示:令g(![]() )=af(
)=af(![]() )+b,
)+b,
则下列关于函数g(![]() )的叙述正确的是
)的叙述正确的是
A.若a<0,则函数g(![]() )的图象关于原点对称.
)的图象关于原点对称.
B.若a=-1,-2<b<0,则方程g(![]() )=0
)=0
有大于2的实根.
C.若a≠0,b=2,则方程g(![]() )=0有两个实根.
)=0有两个实根.
D.若a≥1,b<2,则方程g(![]() )=0有三个实根.
)=0有三个实根.
二、填空题(本题每小题4分,共16分)
13.(文科做)设f(x)=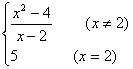 ,则
,则![]()
(理科做)有以下六个命题:
①f(x)=![]() 在[0,1]上连续.
在[0,1]上连续.
②若f(x)是(a,b)内的连续函数,则f(x)在(a,b)内有最大值和最小值.
③若f(x)=![]() ,则
,则![]() =0 ④
=0 ④![]()
⑤![]()
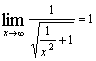 ⑥
⑥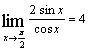
其中正确命题的序号是 (请把你认为正确的命题的序号都填上)
14.已知函数![]() 是奇函数,当
是奇函数,当![]() 时,
时,![]() ,且
,且![]() ,则a等于 .
,则a等于 .
15.(文科做)已知![]() =0,那么x的取值范围是
=0,那么x的取值范围是
(理科做)已知点![]() 其中n的为正整数.设Sn表示△ABC外接圆的面积,则
其中n的为正整数.设Sn表示△ABC外接圆的面积,则![]() =
=
16.已知函数![]() ,
,
那么![]() ▁▁▁▁▁▁
▁▁▁▁▁▁
三、解答题(本题17—21小题每题12分,22小题14分,共74分)
17.(本小题满分12分)给定函数![]() .
.
(Ⅰ)求.![]() ;
;
(Ⅱ)判断![]() 的奇偶性,并证明你的结论.
的奇偶性,并证明你的结论.
18.(本小题满分12分)已知函数![]() 。
。
(1)当![]() 时,求函数
时,求函数![]() 的最小值:
的最小值:
(2)若对任意![]() 恒成立,试求实数
恒成立,试求实数![]() 的取值范围。
的取值范围。
19.(本小题满分12分)已知函数![]() ,求函数
,求函数![]() 的定义域,并讨论它的奇偶性和单调性.
的定义域,并讨论它的奇偶性和单调性.
20. (本小题满分12分)
(文科做)已知函数![]() 在点x=1处有极小值-1.试确定a、b的值.并求出f(x)的单调区间.
在点x=1处有极小值-1.试确定a、b的值.并求出f(x)的单调区间.
(理科做)已知![]() ,函数
,函数![]() 。设
。设![]() ,记曲线
,记曲线![]() 在点
在点![]() 处的切线为
处的切线为![]() 。
。
(1)求![]() 的方程;
的方程;
(2)设![]() 与
与![]() 轴交点为
轴交点为![]() 。证明:
。证明:
(ⅰ)![]() ; (ⅱ)若
; (ⅱ)若![]() 则
则![]()
21.(本小题满分12分)(文科做)已知等差数列{an}的前n项和Sn=n2+n
⑴求![]() ;⑵求
;⑵求![]() .
.
(理科做)已知数列{an}的任何相邻两项an,an+1均是方程x2-bnx+![]() =0的两根,且a1=2.
=0的两根,且a1=2.
⑴求a1, a2, a3, a4;⑵求an;⑶求![]() .
.
22.(本题满分14分)
已知f(x)是定义在[-1,1]上的奇函数,且f(1)=1,若对任意a、b∈[-1,1],a+b≠0有![]() ,
,
(Ⅰ)判断函数f(x)在[-1,1]上是增函数还是减函数,并证明你的结论;
(Ⅱ)解不等式![]() ;
;
(Ⅲ)若f(x)≤![]() ,对所有x∈[-1,1],a∈[-1,1]恒成立,求实数m的取值范围。
,对所有x∈[-1,1],a∈[-1,1]恒成立,求实数m的取值范围。
月考
一、选择题答题栏:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | 文B理A | A | C | B | A | C | 文B理C | C | D | D | B |
二、填空题答题
13. 文4,理4
14. 5
15. 文x>-0.5, 理4π
16. 3.5
三、解答题(本题17—21小题每题12分,22小题14分,共74分)
17.(Ⅰ)求.![]() =lg(x+
=lg(x+![]() )
)
(Ⅱ)![]() 奇
奇
18.(1)3.5
(2)![]() >-3
>-3
19.(本小题满分12分)![]() 的定义域(-1,0)∪(0,1),奇函数,在(-1,0)和(0,1)都单调递减
的定义域(-1,0)∪(0,1),奇函数,在(-1,0)和(0,1)都单调递减
20.文科a=![]() ,b=-
,b=-![]()
(理科(1)![]() 的方程y=-
的方程y=-![]()
(2)略
21.理科:.
⑴a1=2, a2=![]() , a3
, a3![]() , a4
, a4![]() ;⑵an
;⑵an ;⑶
;⑶![]() =4.5.
=4.5.
22.(Ⅰ)函数f(x)在[-1,1]上是增函数
(Ⅱ)[-2.5,-1]
(Ⅲ){mm≥2,或m≤-2,或m=0}