高三数学专题十二探索性问题练习

高三数学专题十二探索性问题练习

跟踪练习

一、选择题

1．已知集合M={xx=,k∈Z}，N={xx=,k∈Z },P={xx=kπ+,k∈Z }，则下列关系成立的是（　　）

A．PNM　　　　　　　 B．P=NM　　　　　　　　 C．PN=M　　　　　　　　 D．P=N=M

2．在△ABC中，sinA>sinB是A>B成立的（　　）

A．充分非必要条件　　　　　　　　　　　　　B．必要非充分条件

C．充要条件　　　　　　　　　　　　　　　　　　D．既不充分也不必要条件

3．幂函数f(x)与g(x)的图像分别过点(3,9)与(8,32)，则不等式f(x)≥g(x)的解集是（　　）

A．(-∞,0∪[1,+∞　　　　　　　　　　　　B．(,-∞,1

C．(-1,1　　　　　　　　　　　　　　　　　　　　 D．(-1,0∪[1,+∞

4．若sinθ·cosθ=,且<θ<，则cosθ-sinθ的值为（　　）

A．-　　　　　　　　　　　　B．　　　　　　　　　　　　　C．-　　　　　　　　　　　　　　D．

5．已知直二面角α—l—β，直线mα，直线nβ，且m、n均不与直线l垂直，则（　　）

A．m与n不可能垂直，但可能平行　　　　　　　　B．m与n可能垂直，但不可能平行

C．m与n可能垂直，也可能平行　　　　　　　　　 D．m与n不可能垂直，也不可能平行

6．双曲线-(y-1)²= -1的两个焦点坐标是（　　）

A．(4,1)、(0,1)　　　　　　B．(2,3)、(2,-1)　　　　　 C．(3,1)、(-1,1)　　　　　 D．(2，4)、(2,0)

7．已知a>a²>b>0,m=log_b,n=log_a,p=log_ab,g=log_ba,则m、n、p、g的大小关系是（　　）

A．g<n<m<p　　　　　　　 B．n<m<p<g　　　　　　　　C．n<g<m<p　　　　　　　 D．n<g<p<m

8．使不等式arccosx>arccos(1-x)成立的x的取值范围是（　　）

A．(0,1)　　　　　　　　　　　B．[0, 　　　　　　　　 C．(0, )　　　　　　　　　D．(-1, )

9．在(1+x)²+(1+x)⁶+(1+x)⁷的展开式中，含x⁴项的系数是等差数列a_n=3n-5的（　　）

A．第2项　　　　　　　　　 B．第11项　　　　　　　　　C．第20项　　　　　　　　 D．第24项

10．极坐标方程是ρ=asinθ和ρ=bcosθ的两个圆的圆心距是（　　）

A．　　　　　　 B．　　　　 C．ab　　　　　　　　　　　　　 D．a+b

11．不等式<2x+a(a>0)的解集是（　　）

A．{xx>0或x< -a}　　　　　　　　　　　　　　　　　　B．{x -<x<a}

C．{x0<x≤a}　　　　　　　　　　　　　　　　　　　　　　　　D．{x-a≤x< -a或0<x≤a}

12．9位师范大学毕业生，其中3男6女，统一分配到三所高级中学，使每所中学恰分到1男2女，则可能的分案的种数是（　　）

A．P₃³C₉³C₆³　　　　　　　 B．C₆³C₄²（P₃³）²　　　　　　　C．540　　　　　D．720

二、填空题

13．函数y=sin²x+sinx·cosx的值域是　　　　　　　　　　　　　。

14．已知定点A(-2),F是椭圆+=1的右焦点，点M在椭圆上移动，则当AM+2MF取最小值时，点M的坐标是　　　　　　　　　　　　　　。

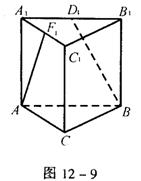
15．如图12-9，ABC—A₁B₁C₁是直三棱柱∠BCA=90°，D₁、F₁分别是A₁B₁、A₁C₁的中点，若BC=CA=CC₁，则BD₁与AF₁所成角的余弦值是　　　　　　　　　　　。

16．若(x²-)ⁿ的 展开式中含x的项为第6项，设(1-x+2x²)ⁿ=a₀+a₁x+a₂x²+…+a_2nx²ⁿ,则a₁+a₂+a₃+…+a_2n=　　　　　　　　 。

三、解答题

17．设0<θ<2π，复数z=1-cosθ+isinθ,u=a²+ai,zu是纯虚线(a∈R)，问w=z²+u²+2zu能否为正实数？为什么？

18．四面体ABCD中，AD=，其余的各棱长均为1，那么互相垂直的面有哪几对？并证明你的结论。

19．由下列各式：1>,1++>1,1++…+>,1++…+>2，你能得出怎样的一般结论？证明你的结论。

20．过点B（1，1）能否作直线m，使m与双曲线x²-=1交于两点Q₁、Q₂，且B是线段Q₁Q₂的中点，说明理由。

21．在△ABC中，∠A，∠B，∠C的对边分别为a,b,c，且b,a,c成等差数列，b≥c，已知B(-1,0),C(1,0)。

（1）求顶点A的轨迹L；

（2）是否存在直线m，使m过点B并与曲线L交于不同的两点P、Q，且PQ恰好等于原点到直线m的距离的倒数？若存在，求出m的方程，若不存在，说明理由。

22．设0<a<1，数列{a_n}是首项为a，公比为-a的等比数列，b_n=a_nlga_n，是否存在自然数M，使得对任意的自然数n，都有b_n≤b_M?证明你的结论。

参考答案

1.A　2.C  3.A　4.C　5.A  6.B　7.C　8.B  9.C　10.B　11.C　12.C　13.[ ,]　14.(2,)　15. 　16.255

17.[解]　不能，假定w为正实数，w=(z+u)²,则z+u为非零实数，z+u=1-cosθ+a²-i(sinθ+a), ∴sinθ+a=0, ∴a= -sinθ　①，又由zu=[(1-cosθ)a²-asinθ]+i[a(1-cosθ)+a²sinθ]为纯虚数，则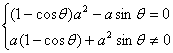　∴a≠0且a=　②

由①②得-sinθ=　∵a≠0,sinθ≠0∴cosθ=2，这不可能。

18．[解]　平面ABD⊥ACD，取AD中点M，可证∠BMC=90°。

19．[解]　1+++…+>且数学归纳法证n=1成立，设n=k成立，1+++…+>,则n=k+1时，左=（1+++…+）+>

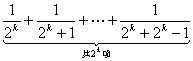+>+=即n=k+1时亦成立，以下略

20．[解]　设直线m存在，且与双曲线交于点Q₁（x₁,y₁）Q₂ (x₂,y₂)，则由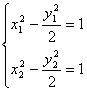可得到: （x₁-x₂）（x₁+x₂）+（y₁-y₂）（y₁+y₂）=0　①, ∵x₁+x₂=2, y₁+y₂=2，若x₁=x₂，直线为x=1显然x=1不符题设条件，所以x₁≠x₂，因此由①得=2即直线的斜率为2，∴直线m的方程为y=2x-1

但是实际上方程组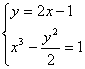无解，即直线与双曲线无交点。

∴满足条件的直线m不存在。

21．【解】　（1）由题设知b+c=2a，BC=2, ∴AB+AC=b+c=2a=2BC=4,又b≥c，故由椭圆的定义知，点A的轨迹L是左半个椭圆（去掉左顶点），轨迹方程为：+=1（-2<x≤0）。

（2）假设存在直线m满足题意，①当m斜率存在时，设m的方程为y=k(x+1)，把它代入椭圆方程，消去y得(4k²+3)x²+8k²x-12=0，设P(x₁,y₁)Q(x₂,y₂)，则x₁+x₂= -，x₁·x₂=，又由x₁≤0,x₂≤0，即x₁x₂≥0, ∴k²≥3所以

PQ==

设原点O到直线m的距离d=,∵PQ=,∴=，得k²=

<3，这与k²≥3矛盾，表明直线m不存在。

②当斜率不存在时，m的方程为x= -1，此时PQ=y₁-y₂=3,d=1PQ≠，所以不满足题设，综上，满足题设的条件不存在。

22．[解]　存在，只要取M=2[]，其中[]表示不超过的最大整数，由题意a_n= (-1)^n-1aⁿ

∵b_n=a_nlga_n=(-1)^n-1naⁿlga　 ∵0<a<1, ∴lga<0

∴当n为奇数时，b_n<0

当n为偶数时，b_n>0

若存在M，使b_n<b_m恒成立，则M为偶数，且只需考虑n为偶数的情况。

设M=2k，则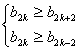即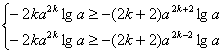

注意：lga<0，得≤k≤即-1≤k≤，k为整数。

∴k=[],M=2k=2[]（符号[x]表示x的整数部分）