高中学生学科素质训练
高三数学综合测试题(2)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间120分钟.
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一
项是符合题目要求的.
1.记集合![]() ,
,
若![]() ,点
,点![]() ,则
,则![]() 的最大值与最小值分别是 ( )
的最大值与最小值分别是 ( )
A.1,-5 B.4,-5 C.13,-20 D.15,-25
2.已知![]() ,函数
,函数![]() 的图象与
的图象与![]() 的图象关于直线
的图象关于直线![]() 对称,
对称,
则g(11)等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.函数![]() 的最小正周期是 ( )
的最小正周期是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
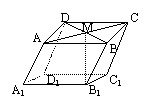 4.如图,在平行六面体ABCD—A1B1C1D1中,M为AC与BD的交点,若
4.如图,在平行六面体ABCD—A1B1C1D1中,M为AC与BD的交点,若![]() ,
,
![]() ,则下列向量中与
,则下列向量中与![]() 相等的向量是 ( )
相等的向量是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.用5,6,7,8,9组成没有重复数字的五位数,其中恰有一个奇数夹在两个偶数之间的
五位数的个数是 ( )
A.120 B.72 C.48 D.36
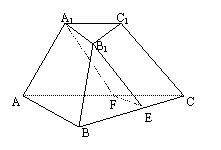 6.如图,在正三棱台A1B1C1—ABC中,A1B1∶AB=2∶3
6.如图,在正三棱台A1B1C1—ABC中,A1B1∶AB=2∶3
截面A1B1EF//CC1,则截面将正三棱台分成两部分的体
积![]() 之比为
( )
之比为
( )
A.19∶12 B.7∶12
C.4∶9 D.1∶5
7.中心在原点,以坐标轴为对称轴的双曲线的渐近线与准线交于![]() ,则双曲线的标
,则双曲线的标
准方程是 ( )
A.![]() B.
B.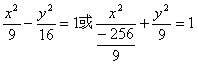
C.![]() D.
D.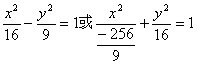
8.如果![]() ,则k的值等于 ( )
,则k的值等于 ( )
A.1 B.2 C.3 D.4
9.函数![]() 有 ( )
有 ( )
A.最大值3,最小值2 B.最大值5,最小值3
 C.最大值5,最小值2 D.最大值3,最小值
C.最大值5,最小值2 D.最大值3,最小值![]()
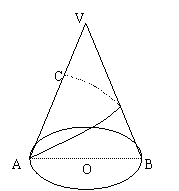
10.已知圆锥SO,AB是底面圆O的直径,AB=8,VA=12,
C是VA的中点,如图,由A绕圆锥一周到C的最短距
离是 ( )
A.![]() B.
B.![]()
C.![]() D.不存在
D.不存在
11.在等差数列{an}中,![]() 且
且![]() ,则Sn中最大的是 ( )
,则Sn中最大的是 ( )
A.S21 B.S20 C.S11 D.S10
12.已知![]() 是奇函数,
是奇函数,![]() 是偶函数,且
是偶函数,且![]() ,则
,则![]()
等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
13.过直线![]() 和
和![]() 的交点,且与y轴夹角为
的交点,且与y轴夹角为![]() 的直线方程为
的直线方程为
.
14.计算![]() ,所得数值等于
.
,所得数值等于
.
15.在![]() 的展开式中,a5的系数是
.(用数字作答)
的展开式中,a5的系数是
.(用数字作答)
16.10人排成一列,现交换部分人的位置,则至少有两个人不在原位置上的排法种数有
.(不要求计算出数值)
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
已知函数![]() 在[-5,0]上有最小值-3,且
在[-5,0]上有最小值-3,且![]() .试比较
.试比较
![]() 和
和![]() 的大小.
的大小.
18.(本小题满分12分)
已知数列![]() 中,
中,![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:![]() 对一切正整数n都成立;
对一切正整数n都成立;
(Ⅲ)求:函数![]() 的值域(
的值域(![]() ).
).
19.(本小题满分12分)
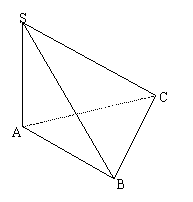 如图,已知三棱锥S—ABC的三条侧棱长均为10,若
如图,已知三棱锥S—ABC的三条侧棱长均为10,若![]() 且
且![]() .
.
(Ⅰ)求证:平面SAB⊥平面ABC;
(Ⅱ)求:三棱锥S—ABC的体积.
20.(本小题满分12分)
某厂有保留下来的一面旧墙长28米,现准备利用这面旧墙的一段为一面墙,建造平面
图形为矩形,面积为504平方米的厂房,工程的条件是:
(Ⅰ)修1米旧墙的费用是造1米新墙费用的25%;
(Ⅱ)拆去旧墙1米用所得材料建1米新墙费用是造1米新墙费用的50%;
(Ⅲ)建门窗的费用与建新墙的费用相同,因此不再考虑.
问如何利用旧墙才能使建墙费用最低.
21.(本小题满分12分)
设函数![]() 是奇函数,对于任意
是奇函数,对于任意![]() 都有
都有![]() 且
且![]() 时,
时,
![]() .
.
(Ⅰ)试问在![]() 时
时![]() 是否有最值?如果有,求出最值;如果没有说明理由.
是否有最值?如果有,求出最值;如果没有说明理由.
(Ⅱ)解关于x的不等式.![]() ,其中
,其中![]() .
.
22.(本小题满分14分)
如图,已知椭圆中心在原点,准线为![]() ,如果直线
,如果直线![]() 与椭圆的交点
与椭圆的交点
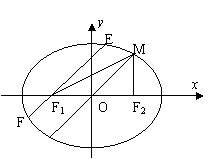 在x轴上的射影恰为椭圆的焦点,求此椭圆方程.并求过焦点F1与直线
在x轴上的射影恰为椭圆的焦点,求此椭圆方程.并求过焦点F1与直线![]() 平行
平行
的弦EF的长.
高三数学综合测试题参考答案
(二)
一、选择题 1.C 2.A 3.B 4.A 5.D 6.B 7.D 8.D 9.C 10.C 11.B 12.D
二、填空题
13.![]() 14.
6 15.207 16.
14.
6 15.207 16.![]()
三、解答题
17.由![]() 知抛物线
知抛物线![]() 的对称轴为x=2.
由此得
的对称轴为x=2.
由此得![]() .
.
当![]() 是减函数,所在在[-5,0]上,当x=0时,
是减函数,所在在[-5,0]上,当x=0时,![]() 有最小值-3,故c=-3.
有最小值-3,故c=-3.
∴所求函数为![]()
![]()
![]() ;
;![]() ;
;![]() .
.
18.(1)当![]() 假设当n=k时,
假设当n=k时,![]() 成立,当
成立,当![]() 时,
时,
![]() ,由此知对
,由此知对![]() 时有
时有![]()
(2)因为![]() ,所以
,所以![]() ,即有
,即有![]()
![]()
(3)由![]() 有
有![]() ,因此
,因此![]() 的值域是
的值域是![]()
19.(1)在![]() 同理
同理
![]() 因为
因为![]() ,所以AC2+BC2+AB2,即△ABC
,所以AC2+BC2+AB2,即△ABC
是直角三角形(∠ACB=90°).又SA=SB=SC=10,则S在底面的射影O为△ABC的外心,由△ABC
|
(2)可求得![]()
![]()
20.设保留旧墙x米,则应拆去旧墙(28-x)米用材料重建新墙.另外,还应建造新墙![]()
米.假设每米新墙造价为1个价格单位,则建墙的总造价为
![]() .
.
当且仅当![]() ,即x=24时取等号. ∴y有最小值70. 答:旧墙应保留24米时,建墙费用最低.
,即x=24时取等号. ∴y有最小值70. 答:旧墙应保留24米时,建墙费用最低.
21.(1)由![]() 则
则
![]() 因为
因为![]() 时,
时,![]()
即![]() 上单调递减.
上单调递减.
![]() 有最大值为
有最大值为![]() .
.
x=3时,![]() 有最小值为
有最小值为![]() .
.
(2)由原不等式,得![]() 即
即![]()
![]()
![]()
由![]() 上单调递减,所以
上单调递减,所以![]()
①当![]() 时,不等式的解集为
时,不等式的解集为![]()
②当![]() 时,不等式的解集为
时,不等式的解集为![]()
③当![]() 时,不等式的解集为
时,不等式的解集为![]() .
.
22.由直线![]() 的斜率
的斜率![]() 知,可设
知,可设![]() .所以
.所以
![]()
![]() 所求椭圆方程为
所求椭圆方程为![]() .
.
由EF平行于直线![]() 所以它的方程为
所以它的方程为![]()
由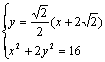 消去y,得
消去y,得![]() 设
设![]() ,
,
![]()
![]()